Dossier de Bernard Vitrac sur les géomètres de la Grèce antique - Chapitre 2 : Le cas Hippocrate : un premier scandale en géométrie?

Encart 2 : les lunules d'Hippocrate

 

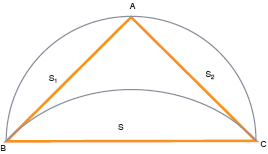
Dans la construction de ses trois lunules Hippocrate combine le principe (H) avec des relations métriques simples pour en déduire des égalités entre segments de cercles.

Lunule 1

ABC est un demi carré inscrit dans le demi-cercle ABC. Sur BC on construit un segment S, semblable aux segments s1 et s2 décrits sur AB et AC.

Puisque l'angle en A est droit on a :

BC2=AB2+BC2 (I. 47).

Et donc, d'après le principe H, on a :

S = s1 + s2.

 

Lunule 2

ABCD est un trapèze tel que:

BA=AD=DC

et BC vérifie :

BC2=3AB2.

Sur BC on construit un segment S, semblable aux segments s1, s2 et s3 décrits sur BA, AD et DC.

Puisque

BC2=BA2+AD2+DC2

on a donc :

S=s1+s2+s3.

Lunule 3

EKBH est un trapèze tel que:

EK=KB=BH.

Hippocrate impose que la droite EZ vérifie : 

EZ2 = (3/2).KB2.

Sur EH on construit un segment S, semblable aux segments s1, s2 et s3 décrits sur EK, KB et BH. Les segments EZ, ZH découpent des segments t1, t2, semblables à S et donc aux s1, s2 s3.

A cause de la condition imposée à EZ, on a:

t1 + t2 = s1 + s2 + s3.

 

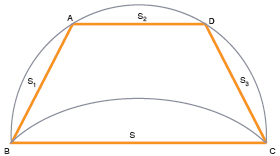
Grâce à ces égalités entre segments de cercle, les trois lunules ainsi construites sont quarrables. En effet :

• Si, du triangle ABC, on retranche le segment S et qu'on ajoute les segments s1 et s2 à ce qui reste, on obtient la lunule 1. Comme ce qu'on ajoute est égal à ce que l'on retranche, la lunule 1 est égale au triangle ABC.

• Si, du trapèze ABCD, on retranche le segment S et qu'on ajoute les segments s1, s2 et s3 à ce qui reste, on obtient la lunule 2. Pour la même raison, la lunule 2 est égale au trapèze ABCD.

• Si de la réunion des trois triangles EKZ, ZKB, BZH, on retranche les segments t1 et t2 et qu'on ajoute les segments s1, s2 et s3 à ce qui reste, on obtient la lunule 3. Donc celle-ci est égale à la réunion des trois triangles.

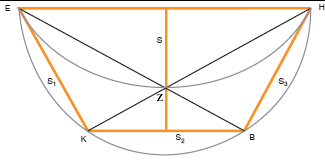
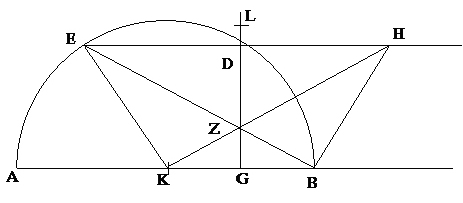
Nous n'avons évoqué qu'une partie du fragment d'Hippocrate. Il montre ensuite comment quarrer la somme d'une quatrième lunule (définie selon le procédé du cas n°1 mais à partir du demi hexagone régulier plutôt que du demi carré) et d'un cercle. Il vérifie aussi que les circonférences extérieures des trois lunules quarrées sont respectivement égale à, plus grande que, plus petite que celle du demi-cercle. Reste une dernière subtilité, dans la construction de la troisième lunule.

Pour ce faire Hippocrate part d'un demi-cercle de diamètre AB, de centre K. Soit G le milieu de KB et GD,  perpendiculaire à AB. Puis il demande que l'on place EZ entre la circonférence ADB et la perpendiculaire GD, de telle manière que : EZ2 = (3/2).KB2 et qu'elle s'incline vers B.Autrement dit EZ a une longueur parfaitement déterminée et son prolongement, du côté de Z, doit passer par B. On appelle "neusis" ce genre de construction.

On prolonge EZ vers B; on joint KE, BE. On mène EH parallèle à AB. On joint KZ que l'on prolonge jusqu'à ce qu'elle coupe ladite parallèle en H. Le trapèze EKBH a trois côtés égaux. On montre qu'il est inscriptible dans un cercle. Le centre de ce cercle est L.

Ici on peut démontrer qu'elle est réalisable "à la règle et au compas", mais ce n'est pas le cas de toutes les neuseis. Nicomède, à la charnière des III-IIs., introduit une famille de courbes, les conchoïdes — ainsi qu'un instrument pour les tracer — qui permettent l'usage systématique de neuseis.