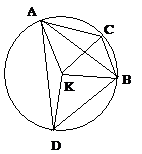Dossier de Bernard Vitrac sur les géomètres de la Grèce antique - Chapitre 2 : Le cas Hippocrate : un premier scandale en géométrie?

Encart 1 : les segments de cercle

 

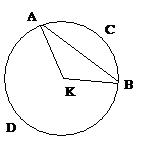
Un segment de cercle est la figure mixtiligne découpée par une sécante dans un cercle.

Figure 1

Soit ABCD un cercle de centre K. On mène la droite AB. La droite AB s'appelle la base du segment. Une sécante découpe en fait deux segments de cercle qu'il est possible de distinguer (si AB n'est pas un diamètre) en disant que l'un, tel ACB est plus petit qu'un demi-cercle, tandis que l'autre, tel ADB, est plus grand qu'un demi-cercle. Au segment on peut associer un secteur (une sorte de part de gâteau), délimité par l'arc AB et les rayons KA, KB.

Intuitivement on voit que dans un cercle donné la grandeur et la forme d'un segment sont déterminées par sa base. Mais on peut se proposer de comparer des segments ou des secteurs appartenant à des cercles inégaux (Fig. 2)

 

Pour les secteurs, il est naturel de dire qu'ils sont semblables quand ils représentent la même part du gâteau, c'est-à-dire quand les angles aux centres AKB et ELF sont égaux. D'autant que si tel est le cas, les triangles isocèles AKB et ELF seront aussi semblables car équiangles.

On peut donc penser à chercher une caractéristique angulaire relative aux segments de cercle. On démontre facilement (Figure 2) que si l'on prend des points C, D, quelconques, l'un sur l'arc AB, l'autre sur l'arc complémentaire, les angles ACB, ADB ne dépendent pas des positions des points C, D sur leurs arcs respectifs.

Figure 2

Ils sont caractéristiques, l'un du segment ACB, l'autre du segment ADB.

 

En utilisant deux propriétés très simples :

• la somme des angles d'un triangle est égale à deux angles droits;

• les angles à la base d'un triangle isocèle sont égaux,

on montre que l'angle ACB est égal à deux droits moins la moitié de l'angle du secteur AKB. Il ne dépend donc pas de la position de C sur l'arc AB. Quant à l'angle ADB, il vaut la moitié de l'angle AKB.

Figure 3

Par conséquent, si on revient à la figure 2 on voit que les angles dans les segments ACB, EDF seront égaux si et seulement si les angles AKB et ELF sont égaux, autrement dit si les secteurs AKB, ELF sont semblables. On dira donc que les segments ACB, EDF sont semblables si leurs angles sont égaux (Euclide, Livre III, Df. 11). On peut penser qu'Hippocrate utilisait la même définition quoique nous n'en sachions rien. Mais il utilisait la notion pour formuler le principe sur lequel étaient fondées ses quadratures (voir Encart 2) :

« Deux segments de cercle semblables ont le même rapport que les carrés décrits sur leur base » (H)

Sur notre figure 2, puisque ACB et EDF sont semblables, le rapport de leurs aires est le même que AB2 : EF2.