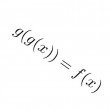CultureMath
Ce résultat est assez connu sous une forme plus faible : période 3 implique période n pour tout entier n. C'est-à-dire qu'une fonction continue, d'un segment dans lui-même, ayant un point de période 3 a nécessairement un point de période n pour tout n. En fait, ceci est une conséquence du théorème de Sharkovskii, qui affirme que si une fonction continue d'un segment dans lui-même a un point de période m (m entier), alors cette fonction a un point de période n pour tout n plus grand que m pour l'ordre de Sharkovskii (ordre sur les entier dont 3 est bien sûr le plus petit élément).
Dans cette conférence destinée aux collégiens et aux lycéens, Cédric Villani nous fait suivre un long fil qui part de la géométrie du plan euclidien, en passant par la théorie des nombres, la topologie, la géométrie fractale, pour nous mener à ses travaux en théorie cinétique des gaz. Il nous montre alors comment cette théorie lui a permis de revenir à la géométrie, non euclidienne cette fois-ci !
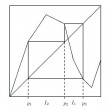
Un petit film de P. Trivic (la Tempête) dans le cadre du "quart-d'heure mathématique" sur les systèmes mélangeants, commenté par le savant géométre Marcel Berger, diffusé sur la 7 le 24 novembre 1990 à 22h30, présentait une séquence particulièrement percutante : Le portrait de Poincaré -initiateur de la théorie du Chaos- était déstructuré par une transformation dite de la pâte feuilletée (on étale la pâte intialement en carré, et on replace les morceaux débordants pour reconstituer le carré). Puis –oh miracle- au bout de 241 opérations dé-structurantes, le portrait de Poincaré réapparaissait "intact".
Quel lien y a t-il entre le rayon des séries entières et celui de leur produit d'Hadamard? L'auteur donne à la façon de Cyrano dans la tirade des nez de multiples applications et illustrations dont une formule donnant la somme du produit d'Hadamard en fonction de celles des deux séries arguments.
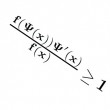
En 1870 Vassili Petrovitch Ermakov découvre des critères très fins de convergence de séries et d'intégrales ; ces critères se retrouvent (de manière anonyme) dans beaucoup d'exercices d'oraux. L'auteur en rappelle l'énoncé en illustrant leur principe.
Inspiré du problème d'agrégation 1949 proposant de rechercher les fonctions g inconnues telles que g(g(x))=f(x) (f donnée), cet article, abondamment illustré par des exemples concrets, montre comment trouver les solutions et donne diverses applications très récentes de cette théorie (réseaux de neuronnes (et le fameux Perceptron), géographie pour la prédiction de l'occupation des sols, recherche des périodes en théorie du chaos, prédiction boursière, technique du laminage en industrie,...).
Il s'agit d'étalonner une jauge de cuve à Mazout cylindrique bombée, horizontale, et d'utiliser du calcul intégral pour établir la formule exacte de cette jauge.
Ce petit addendum de deux pages démontre un résultat simple mais surprenant : si l'on prend n chiffres quelconques, il existe une infinité de puissances de 2 commençant par ces chiffres !
Ce texte part d'une observation expérimentale: quand on calcule une trentaine ou plus de valeurs de 2n , on constate que le premier chiffre est nettement plus souvent "1" que n'importe quel autre. Il arrive dans plus de 30% des cas ! Mais que signifie ce pourcentage ?
Les équations fonctionnelles, par leur diversité, le fait qu'il n'y ait pas de méthode standard ou universelle pour les résoudre, rivalisent aussi bien avec l'arithmétique que la géométrie, pour montrer la richesse des mathématiques. Elles obligent aussi l'étudiant ou le chercheur à appréhender la nécessité d'une argumentation rigoureuse.