Vous pouvez retrouver cette question au format pdf.
Question du jeudi #33 : On considère le pavage du plan par des triangles équilatéraux :
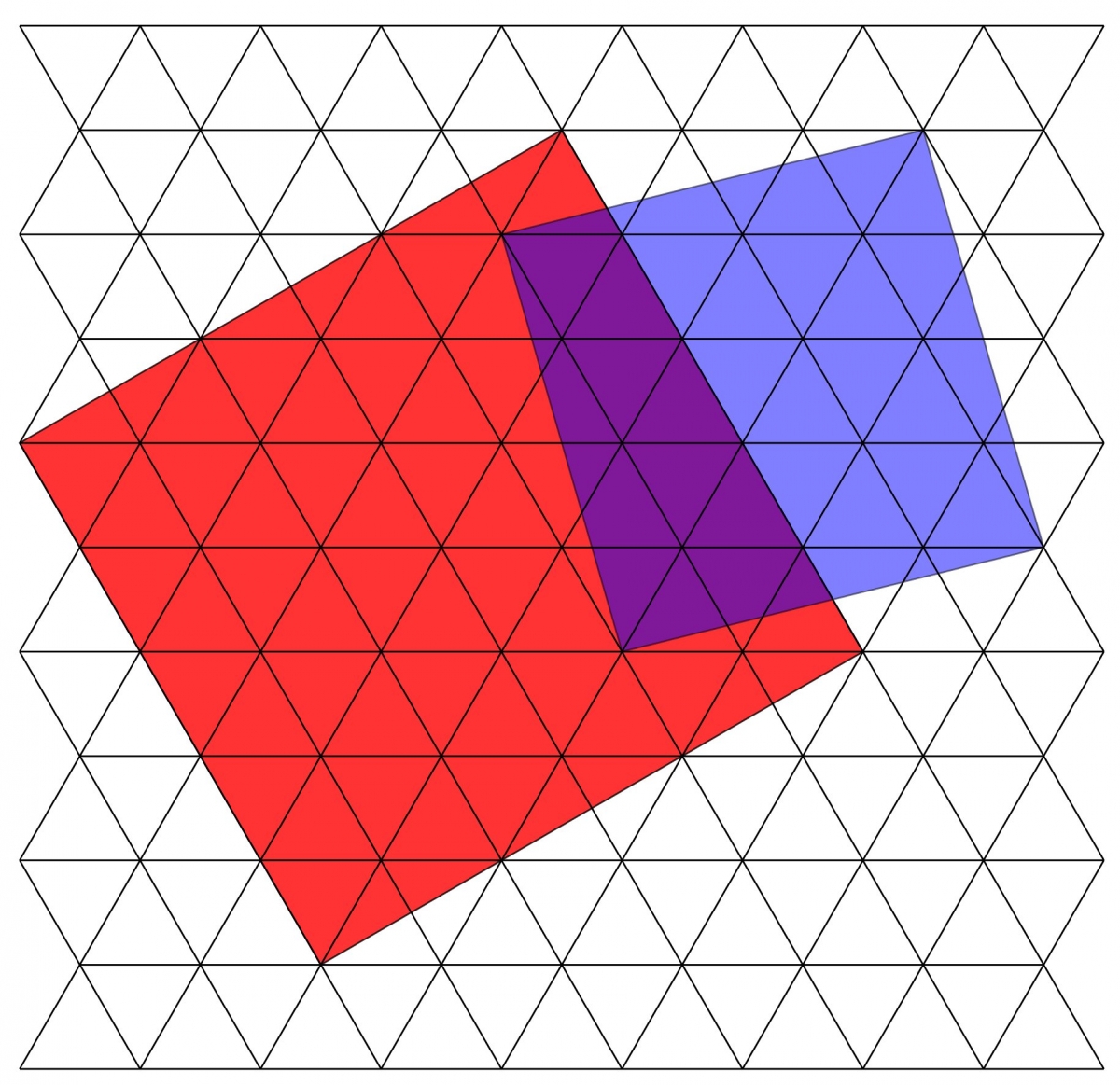
Parmi les sommets des triangles, est-il possible de trouver quatre points formant un carré ?
Ça n'est pas possible. Introduisons des coordonnées dans lesquelles un des triangles a pour sommets $\binom 0 0$, $\binom 0 1$ et $\binom{1/2}{\sqrt 3 / 2}$.
On remarque alors que les sommets des triangles ont pour abscisse des multiples de $1/2$ et pour ordonnée des multiples de $\sqrt 3/2$.
Or, si quatre des sommets formaient un carré, on pourrait le décaler pour que l'un des sommets soient à l'origine du repère. En particulier, les deux sommets adjacents à $\binom 00$ auraient pour coordonnées $\binom x y$ et $\binom {-y} x$ ou $\binom x y$ et $\binom y {-x}$.
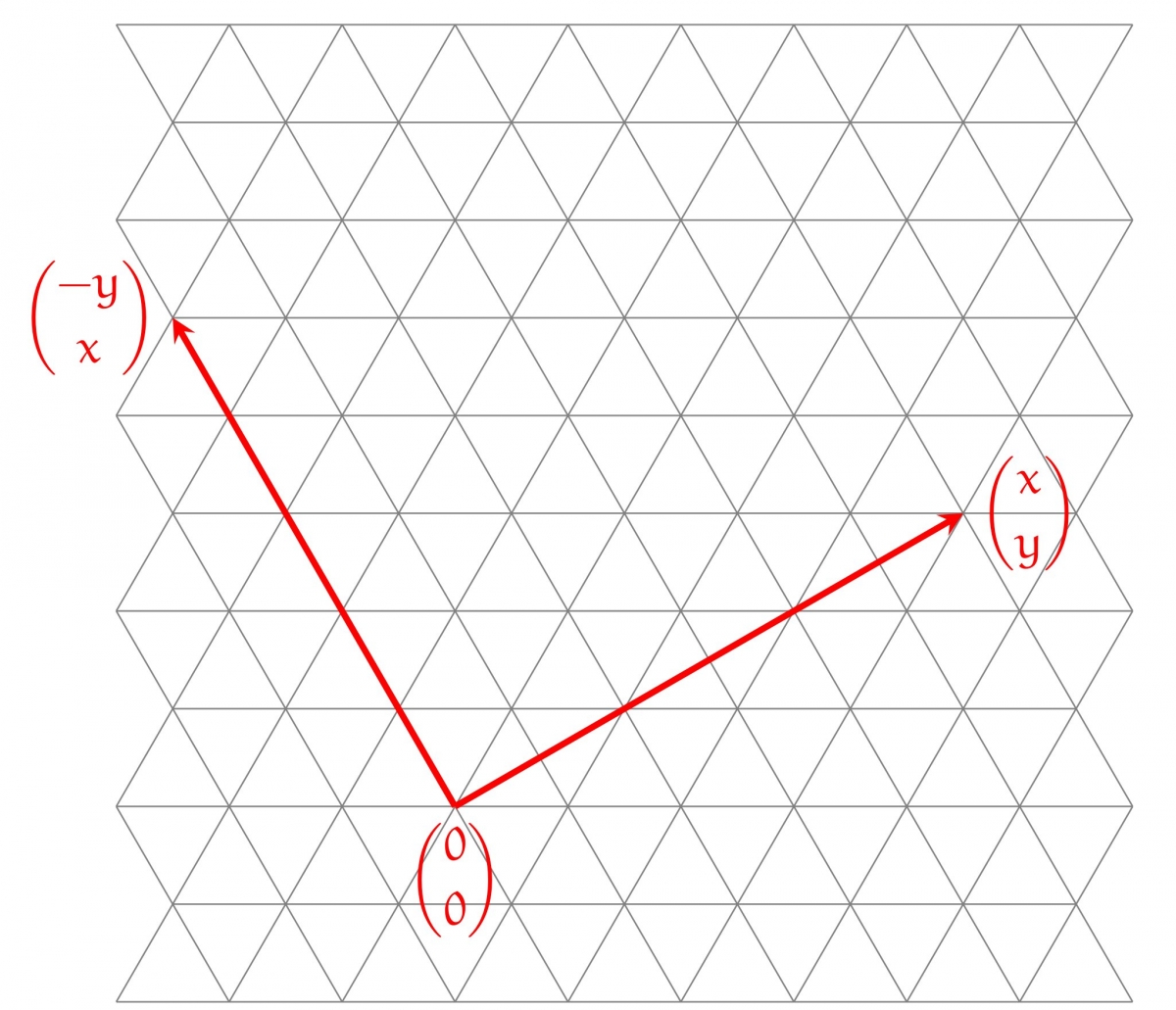
Le problème est que, d'après ce qui précède, $x$ et $y$ doivent être à la fois des multiples entiers de $\frac 1 2$ et $\frac{\sqrt 3}2$~: en particulier,
\[ x = \frac 12 p = \frac{\sqrt 3}2 q, \qquad y = \frac 12 p' = \frac{\sqrt 3}2 q',\]
pour deux entiers $(p,q) \in \mathbb Z^2$.
Comme $\binom x y \neq 0$, $x$ et $y$ ne peuvent pas être tous les deux nuls. Supposons par simplicité que $x \neq 0$ (le cas $y \neq 0$ est similaire). On a donc
\[ \frac{\sqrt 3}2 q = \frac 12 p \quad \text{donc} \quad \frac p q = \sqrt 3,\]
ce qui est impossible car $\sqrt 3$ est un nombre irrationnel.