Vous pouvez retrouver cette question au format pdf.

Question du jeudi #30 : On considère un paquet de jetons de trois couleurs (rouge, vert et bleu). On s'autorise à chaque coup à remplacer deux jetons de couleurs différentes par deux jetons de la troisième couleur. Par exemple, voici une suite de transformations autorisées.

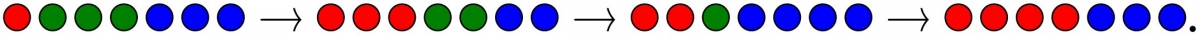
En partant d'une situation avec $1515$ jetons rouges, $1789$ jetons verts et $2015$ jetons bleus, est-il possible de parvenir à une situation où tous les jetons sont de la même couleur ?

Non, c'est impossible.

Notons n_⬤, n_⬤ et n_⬤ le nombre de jetons de ces trois couleurs. À chaque opération, ces nombres sont modifiés d'une des trois façons suivantes :

• ⬤ ⬤ → ⬤ ⬤ : (n_⬤, n_⬤, n_⬤) → (n_⬤ - 1, n_⬤ - 1, n_⬤ + 2) ;
• ⬤ ⬤ → ⬤ ⬤ : (n_⬤, n_⬤, n_⬤) → (n_⬤ + 2, n_⬤ - 1, n_⬤ - 1) ;
• ⬤ ⬤ → ⬤ ⬤ : (n_⬤, n_⬤, n_⬤) → (n_⬤ - 1, n_⬤ + 2, n_⬤ - 1).

Rappelons que deux nombres entiers sont dits congrus modulo $3$ si leur différence est un multiple de $3$, c'est-à-dire si elles produisent le même reste (qui peut être $0$, $1$ ou $2$) quand on pose leur division par $3$.

L'intérêt de cette notion pour notre jeu est que si $n$ est un nombre entier, $n-1$ et $n+2$ sont congrus modulo $3$. Ainsi, en partant de trois nombres qui ne sont pas congrus deux à deux modulo $3$ (comme dans notre exemple, puisque $1515 \equiv 0 \ (\textrm{mod}\ 3)$, $1789 \equiv 1 \ (\textrm{mod}\ 3)$ et $2015 \equiv 2 \ (\textrm{mod}\ 3)$), on ne pourra produire que des triplets de nombres possédant cette propriété. En particulier, on ne pourra jamais arriver à une situation où deux des nombres valent $0$, c'est-à-dire à une situation incolore.