Vous pouvez retrouver cette question au format pdf.

Question du jeudi #19 : On dit qu'un entier $n$ est une anagramme de $m$ si on peut écrire $n$ en permutant les chiffres de $m$. On ne compte pas les 0 non significatifs que l'on peut ajouter à gauche : 330 est une anagramme de 303, mais pas de (0)33.

Une puissance de 2 peut-elle être l'anagramme d'une autre puissance de 2 ?

Si $n = 2^a$ est une anagramme de $m = 2^b$, ils ont particulier le même nombre $r$ de chiffres. Cela signifie que $10^{r-1} \leq n, m < 10^r$. Or, comme $2^4 = 16 > 10$, on ne peut jamais trouver cinq puissances de 2 ayant le même nombre de chiffres. (En fait, le nombre de puissances de $2$ ayant $k$ chiffres vaut toujours 3 ou 4, mais on n'en a pas besoin ici).

Par ailleurs, si deux nombres sont anagrammes l'un de l'autre, la somme de leurs chiffres est la même, et ils sont donc congrus modulo $9$. Or, les puissances de $2$, modulo $9$, sont périodiques de période $6$ : $2^6 = 64 \equiv 1$ (modulo 9) :

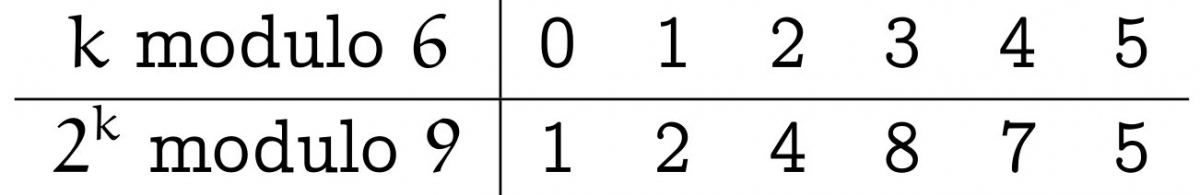
Ainsi, quatre puissances consécutives de $2$ n'auront des sommes de chiffres égales, donc, en particulier, les puissances de $2$ ne sont jamais des anagrammes l'une de l'autre.