Vous pouvez retrouver cette question au format pdf.

Question du jeudi #5 : Étant donné trois droites parallèles $\Delta_1$, $\Delta_2$, $\Delta_3$, construire à la règle et au compas un triangle équilatéral $A_1A_2A_3$ tel que $A_1 \in \Delta_1$, $A_2 \in \Delta_2$ et $A_3 \in \Delta_3$.

Déjà, on se convainc relativement facilement qu'un tel triangle existe. En supposant que la droite $\Delta_2$ est entre les deux autres droites, fixons un point $A_1 \in \Delta_1$ et faisons varier un point $A_3$ sur $\Delta_3$. On voit alors facilement que l'on peut former un triangle équilatéral $A_1 A_2 A_3$, et qu'en faisant varier $A_3$, $A_2$ décrit une droiteEn fait, deux droites : étant donné un segment $A_1A_3$, il y a deux points $A_2$ tels que $A_1A_2A_3$ soit équilatéral : un pour lequel $A_1$, $A_2$ et $A_3$ sont ordonnés dans le sens direct et un pour lequel ils sont ordonnés dans le sens indirect. Dans la suite, on se concentre sur une des deux possibilités. : la solution du problème est à l'intersection de cette droite et de $\Delta_2$.

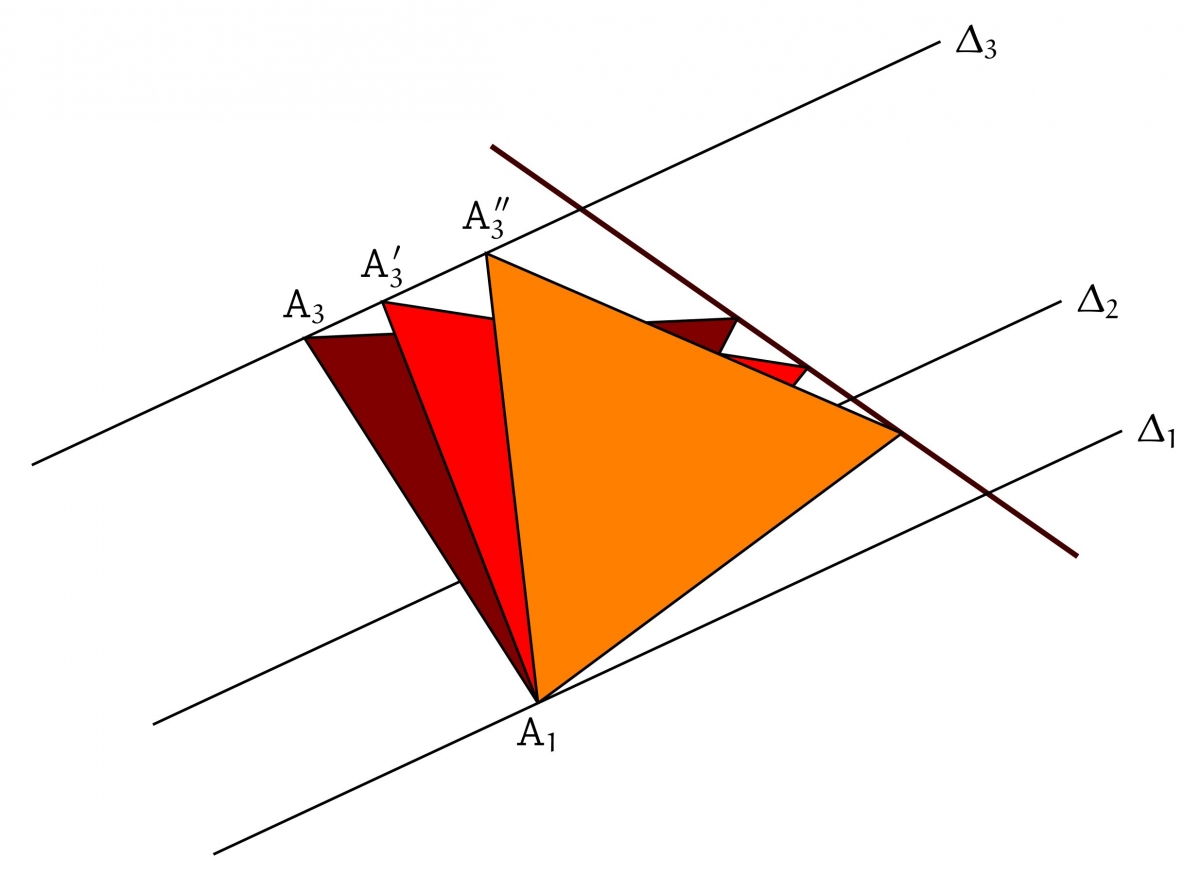
Observons ce qui se passe lorsque le point $A_2$ est sur $\Delta_2$.

Comme $A_1A_2A_3$ est équilatéral, l'angle entre les deux vecteurs $\overrightarrow{A_1A_2}$ et $\overrightarrow{A_1A_3}$ est de 60°. Le point $A_2$ est donc soumis à deux contraintes : il est sur $\Delta_2$ et son image par la rotation de centre $A_1$ et d'angle 60° est sur $\Delta_3$.

Cela permet la construction du triangle : si les droites $\Delta_1$, $\Delta_2$ et $\Delta_3$ sont données, il s'agit de tracer la droite $\Delta_2'$, image de $\Delta_2$ par la rotationParce que nous avons choisi de construire le triangle $A_1 A_2 A_3$ direct. Si nous avions fait l'autre choix, il s'agirait de la rotation d'angle -60° de centre $A_1$ et d'angle 60°. Le point $A_3$ est alors à l'intersection de $\Delta_3$ et $\Delta'_2$.

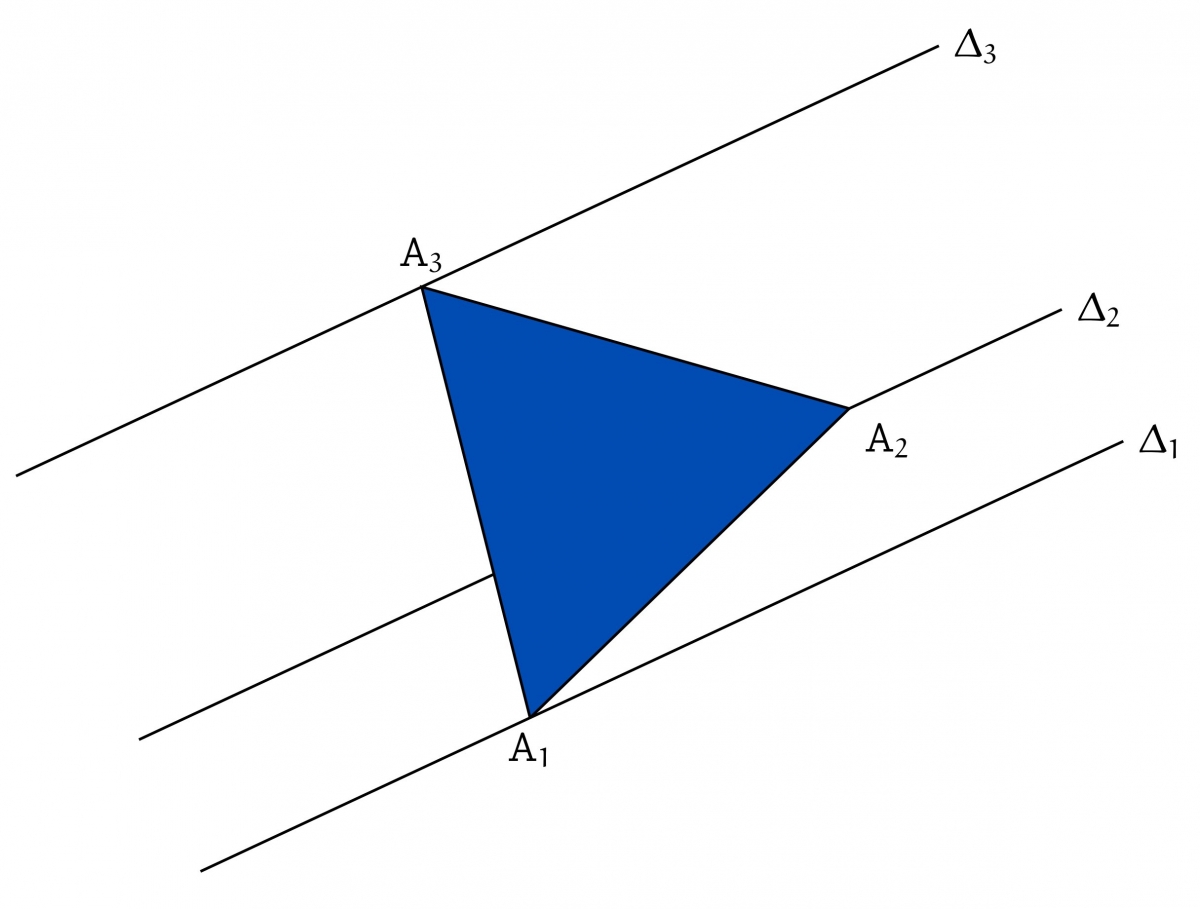
Une solution possible à notre problème est donc la suivante :

1. Placer un point $A_1$ sur $\Delta_1$.
2. Construire la droite $\Delta_2'$ image de $\Delta_2$ par la rotation de centre $A_1$ et d'angle 60°. On appelle $A_3$ le point d'intersection de $\Delta_2'$ et $\Delta_3$ (par construction ces droites ne peuvent pas être parallèles puisque l'angle entre elles est de 60°).
3. Construire le triangle équilatéral (direct) $A_1 A_2 A_3$.

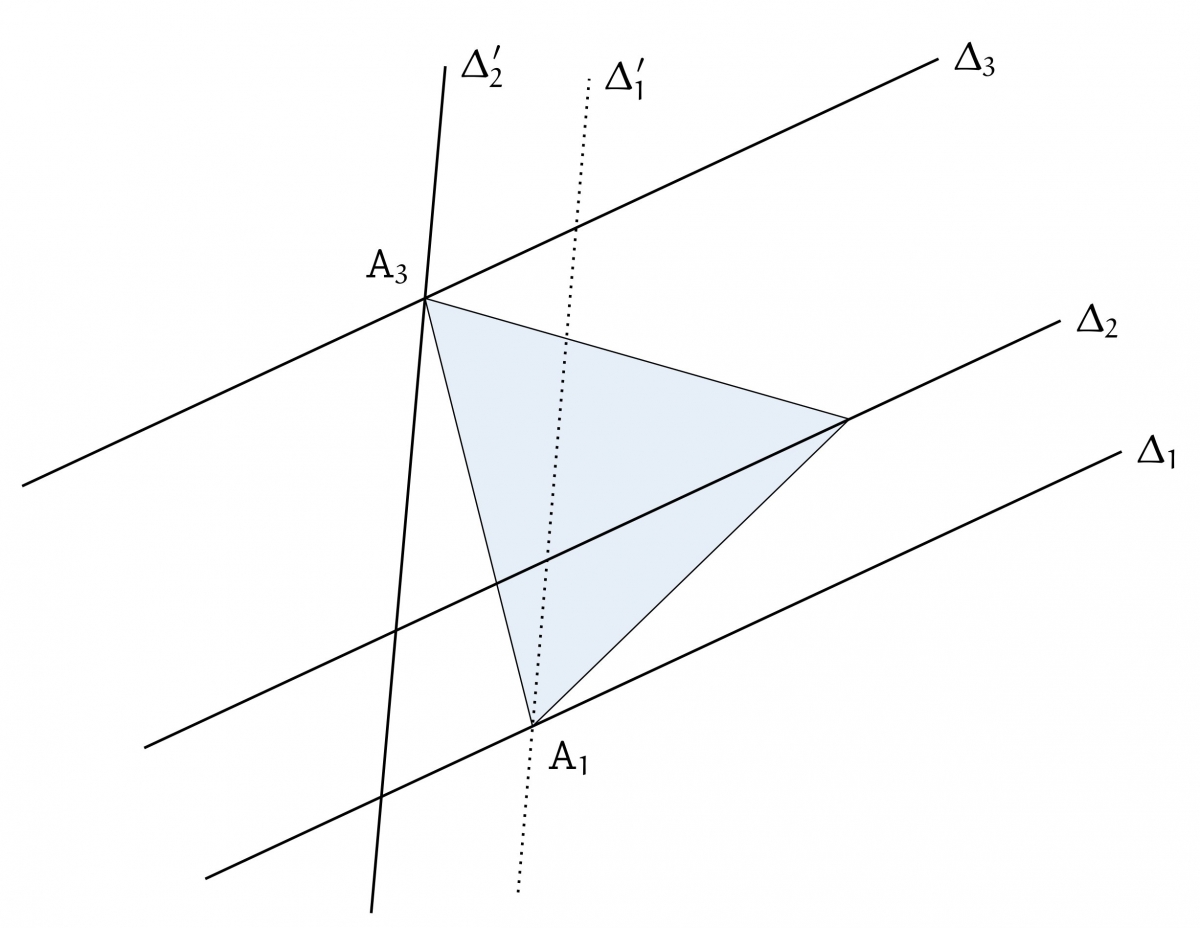
Pour pouvoir effectuer cette construction à la règle et au compas, il suffit de s'assurer qu'étant donné un point $A$ (jouant le rôle de $A_1$) et une droite $\Delta$ (jouant celui de $\Delta_2$), on peut construire l'image $\Delta'$ de la droite $\Delta$ par la rotation de centre $A$ et d'angle 60°. Voilà une possibilité de construction, une fois que l'on sait construire la perpendiculaire à une droite donnée passant par un point donné.Voir par exemple la wikipédia pour un rappel de ces constructions classiques.

But : construire $\Delta'$, image de $\Delta$ par la rotation de centre $A$ et d'angle 60°.

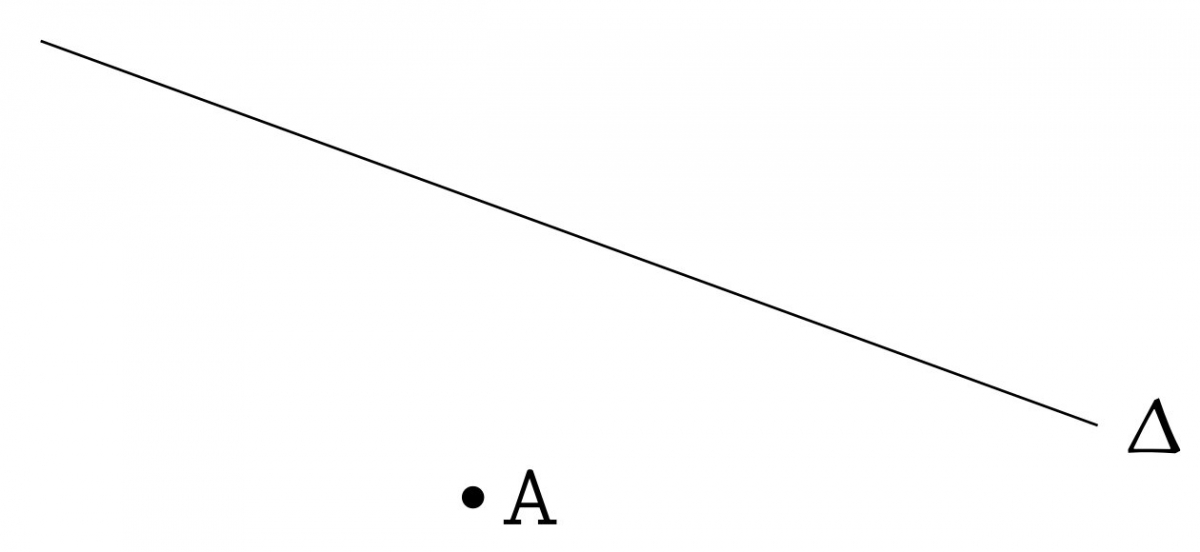
Étape 1 : abaisser la perpendiculaire à $\Delta$ passant par $A$.

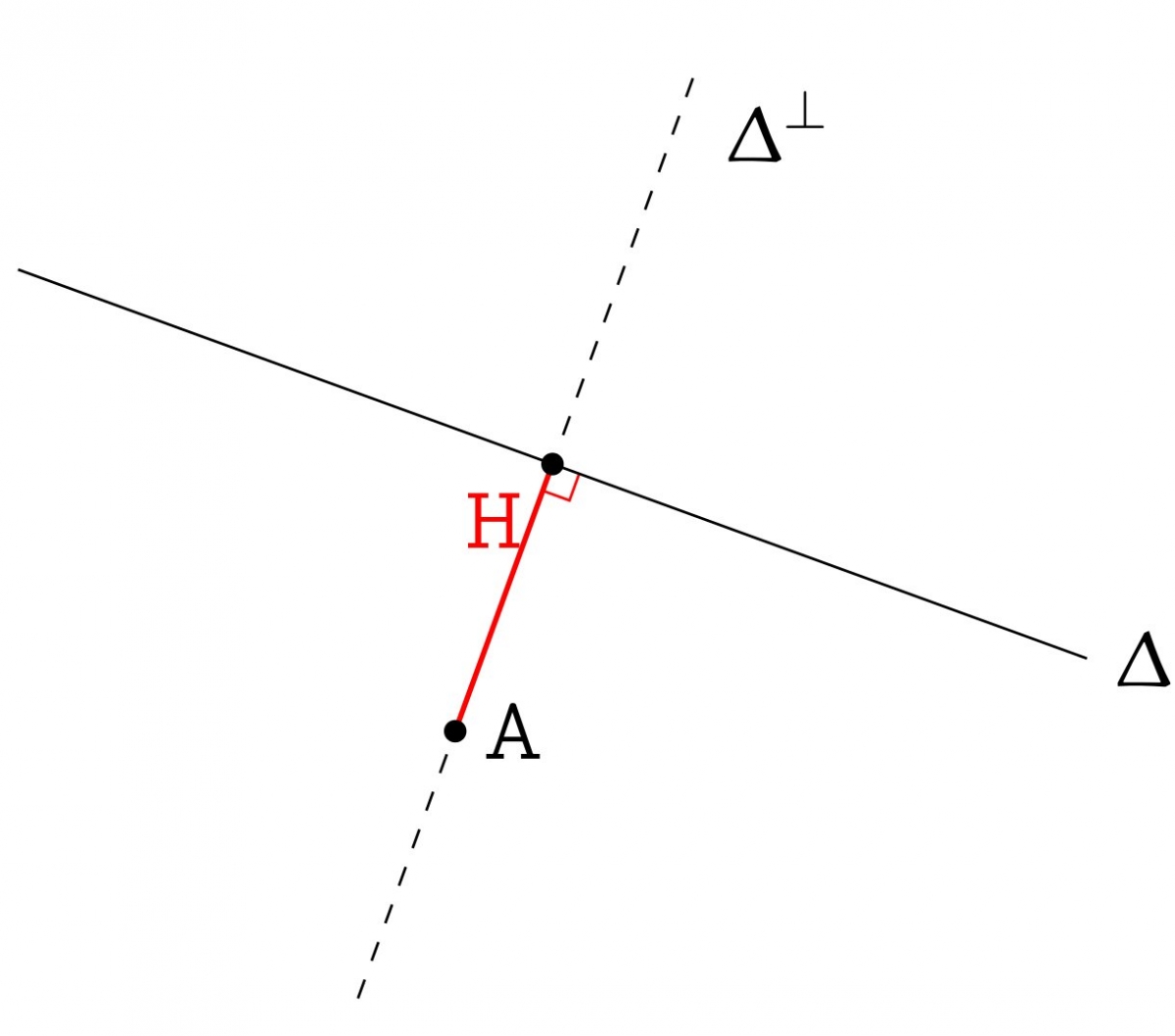
La droite cherchée sera donc perpendiculaire à l'image de $[AH]$ par la rotation de centre $A$ et d'angle 60°.

Étape 2 : construire le triangle équilatéral direct $AHB$.

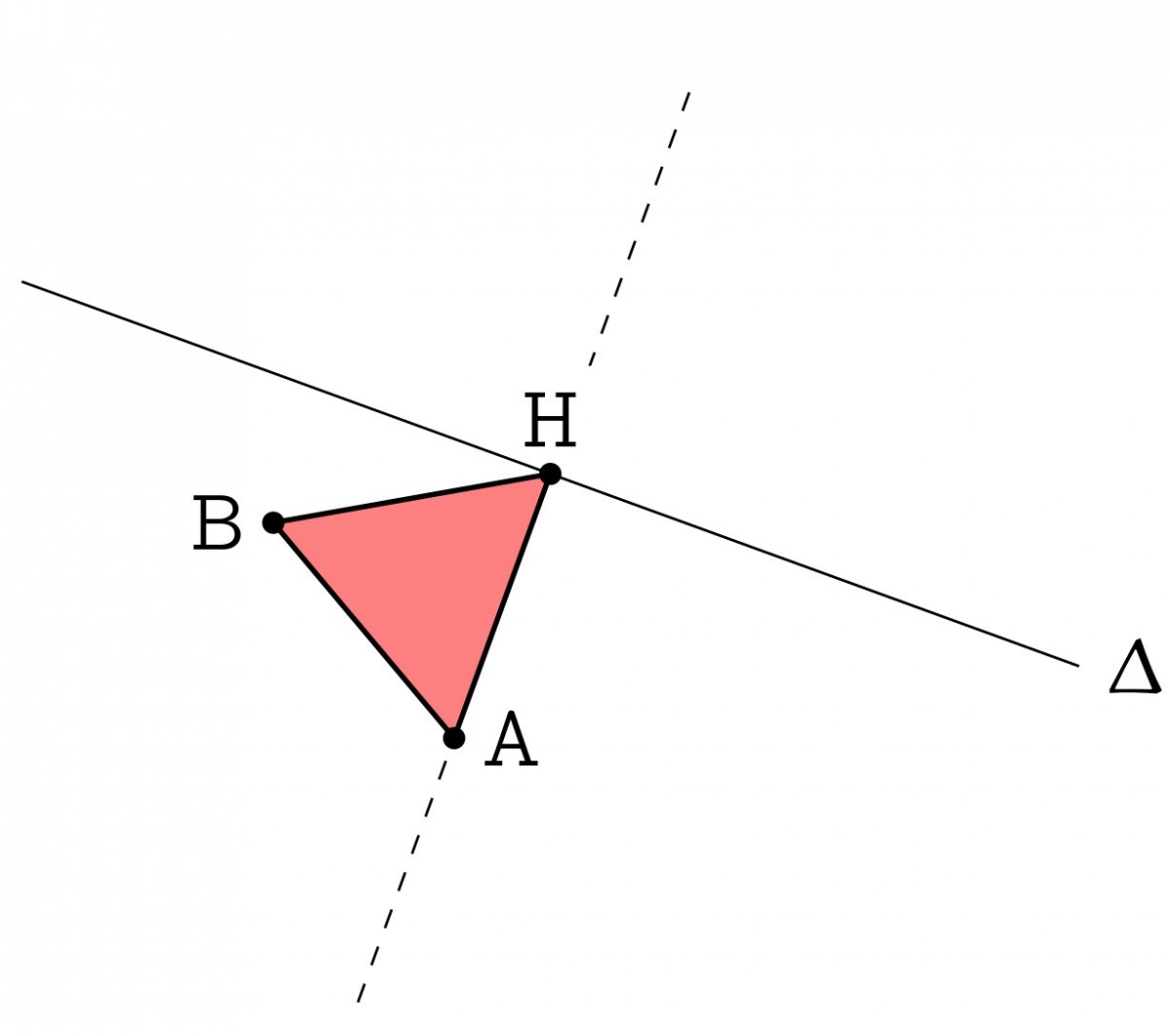
Étape 3 : La droite cherchée est maintenant la perpendiculaire à $[AB]$ passant par $B$.

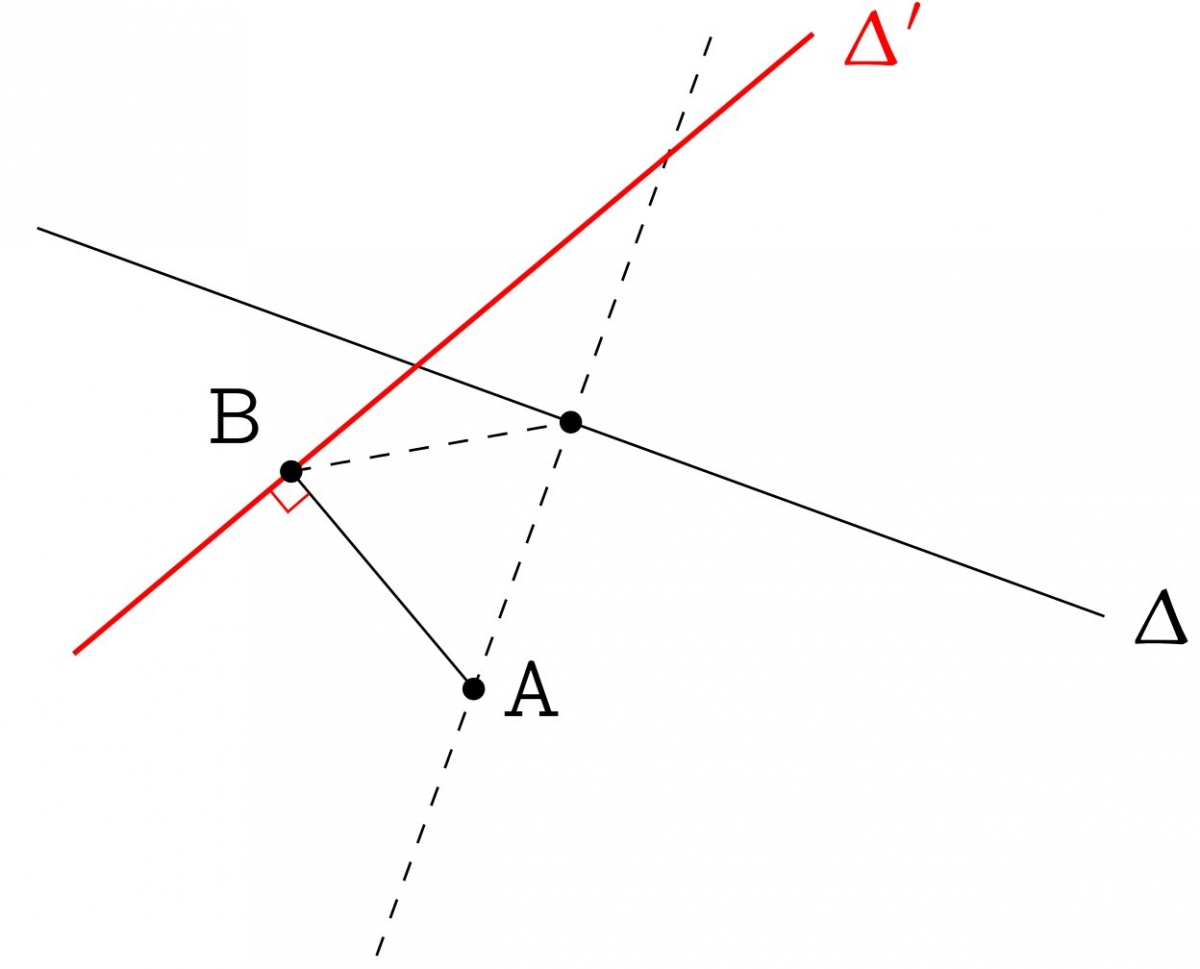
Cela conclut la construction.