Arcus : un simulateur du Rubik's cube
Retour au Sommaire - Retour Article - Retour Encart 4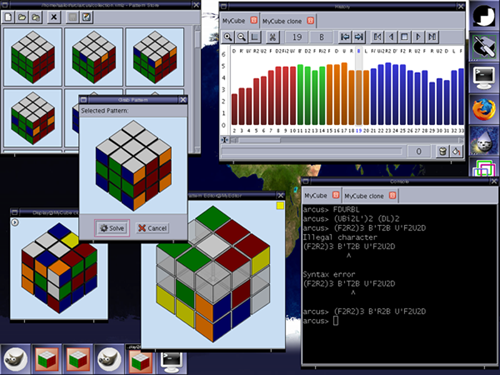
|
Sommaire
|
Pour
une meilleure compréhension des transformations utilisées
dans l'article "Le Rubik's cube, groupe de poche" de Pierre Colmez, le lecteur est vivement le invité à utiliser le logiciel
libre Arcus
qui est un simulateur
du
Rubik's Cube.
Pour cela il faut se rendre sur la page http://sourceforge.net/projects/arcus Puis télécharger (gratuitement) le programme Arcus et l'installer.
Arcus fonctionne avec Java Runtime Environment. Dans le cas où l'environnement Java n'est pas déjà installé, le lecteur trouvera ce programme sur la page http://java.com/en/download/.
Le lecteur lisant l'anglais trouvera toutes les informations utiles au maniement de ce programme de simulation dans la rubrique "Manual" sur la page http://arcus.sourceforge.net/manual.html.
Dans le cas contraire, nous allons préciser les instructions de bases qui permettent de le faire fonctionner.
Dans la première fenêtre intitulée "Arcus", selectionner "File", puis "New Instance".
Trois autres fenêtres s'ouvrent :
- L'une est intitulée "Display" où se trouve le Rubik's cube, que l'on peut manipuler avec le bouton gauche de la souris.
- la seconde intitulée "Console" permet de piloter le Rubik's cube en proposant une série de rotations.
- la troisième intitulée "History" garde en mémoire toutes les transformations effectuées sur le Rubik.
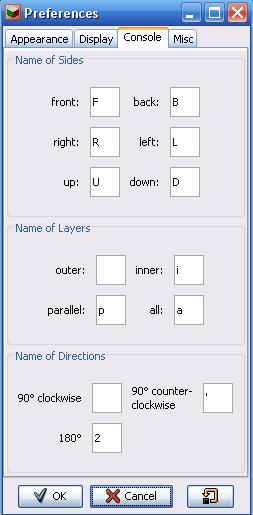
Il est préférable de modifier le nom des faces afin de respecter les conventions de l'article.
Pour cela, dans la fenêtre "Arcus", sélectionner "Tools" puis "Preferences" et "Console".
Pour cela il faut se rendre sur la page http://sourceforge.net/projects/arcus Puis télécharger (gratuitement) le programme Arcus et l'installer.
Arcus fonctionne avec Java Runtime Environment. Dans le cas où l'environnement Java n'est pas déjà installé, le lecteur trouvera ce programme sur la page http://java.com/en/download/.
Le lecteur lisant l'anglais trouvera toutes les informations utiles au maniement de ce programme de simulation dans la rubrique "Manual" sur la page http://arcus.sourceforge.net/manual.html.
Dans le cas contraire, nous allons préciser les instructions de bases qui permettent de le faire fonctionner.
Initialisation
Dans la première fenêtre intitulée "Arcus", selectionner "File", puis "New Instance".

Trois autres fenêtres s'ouvrent :
- L'une est intitulée "Display" où se trouve le Rubik's cube, que l'on peut manipuler avec le bouton gauche de la souris.
- la seconde intitulée "Console" permet de piloter le Rubik's cube en proposant une série de rotations.
- la troisième intitulée "History" garde en mémoire toutes les transformations effectuées sur le Rubik.
Modifier le nom des faces
Il est préférable de modifier le nom des faces afin de respecter les conventions de l'article.
Pour cela, dans la fenêtre "Arcus", sélectionner "Tools" puis "Preferences" et "Console".
 |
 |
|
| Modifier les noms des faces
comme suit : Modifier aussi le contenu de "Name of Layers" - "all" (a en A) |
||
Pour faire afficher les noms des faces sur le cube, sélectionner la fenêtre du Rubik (ou cliquer dessus) et taper sur la barre d'espace.
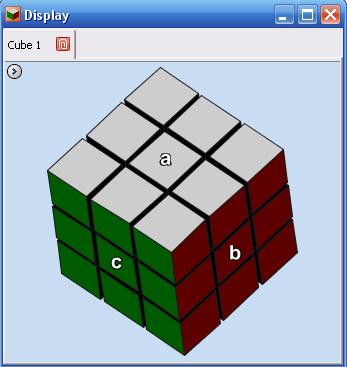
Manipulation virtuelle du Rubik
- Il est possible d'opérer des rotations de tranches directement avec le bouton droit de la souris. Pour cela maintenir pressé le bouton droit de la souris et parcourir les petits carrés formant un coin d'une tranche, dans le sens de rotation souhaitée.
- A l'aide de la "Console"
Les rotations de tranche de 90° dans le sens horaire portent les noms des faces correspondantes a, b, c, d, e, f.
On peut définir dans la fenêtre Arcus / Tools / Preferences/ (Cf. images ci-dessus) le symbole qui permettra de nommer une rotation dans le sens trigonométrique.
a' est le nom de la rotation de 90° dans sens trigonométrique de la tranche de face a.
Remarque: nous choisissons de ne pas modifier la notation initiale car le logiciel ne nous permet pas la notation a-1 utilisée dans l'article.
Les transformations élémentaires de l'article
Mise en place des bords
La mise en place des bords utilise l’élément (a2b)5 de Rub et ses conjugués. Nous avons admis que "cet élément a pour vertu d’échanger yac et yad en échangeant les faces a, et de laisser fixes les autres bords.
Testons cela à partir de la position initiale ( Rubik's cube résolu - une seule couleur par face) proposée par le logociel Arcus.
Les couleurs dans la configuration initiale sont :
| a | blanc |
| b | rouge |
| c | vert |
| d | bleu |
| e | orange |
| f | jaune |
Dans cette configuration initiale on a donc :
yad = bord "blanc-bleu" et yac = bord "blanc-vert"
Ouvrir la fenêtre "Console" et saisir (ba2)5 puis valider.
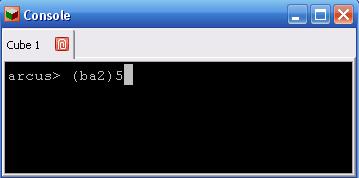
Remarque: le simulateur n'interprête pas la notation mathématique de la composition; il faut donc écrire les composées dans le sens inverse.
On peut alors vérifier que les deux bords yad = bord "blanc-bleu" et yac= bord "blanc-vert" ont été échangés et que les autres bords sont laissés fixes par cette transformation.
Orientations de bords
Nous avons admis que "la transformation d2fbd −1 retourne yad et laisse fixe yac."
De nouveau testons cela à partir du Rubik résolu. Pour cela ouvrir un nouveau cube (Cube 2) dans la première fenêtre intitulée "Arcus", en selectionnant "File", puis "New Instance". Puis sélectionner "Cube 2" et appuyer sur la barre d'espace pour faire apparaître les noms des faces.
De nouveau les couleurs des faces dans la configuration initiale sont :
| a | blanc |
| b | rouge |
| c | vert |
| d | bleu |
| e | orange |
| f | jaune |
Dans cette configuration initiale on a donc :
yad = bord "blanc-bleu" et yac = bord "blanc-vert"
Ouvrir la fenêtre "Console", et sélectionner "Cube 2" puis saisir d'bfd2 et valider.
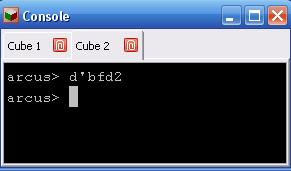
On constate que le bord en yac est resté fixe (bord "blanc-vert") et le bord "blanc-bleu" (qui était en yad ) a simplement été retourné.
Mise en place des coins
La mise en place des coins utilise l’élément (b−1a−1ba)3 de Rub. Nous avons admis que "cet élément a pour vertu de fixer les bords, et d’échanger les coins xabc et xfcb (en échangeant les faces a et f) ainsi que les coins xadb et xdae (en échangeant les faces b et e), tout en laissant fixes les autres."
De nouveau testons cela à partir du Rubik résolu. Pour cela ouvrir un nouveau cube (Cube 3) dans la première fenêtre intitulée "Arcus", en selectionnant "File", puis "New Instance". Puis sélectionner "Cube 3" et appuyer sur la barre d'espace pour faire apparaître les noms des faces.
De nouveau les couleurs des faces dans la configuration initiale sont :
| a | blanc |
| b | rouge |
| c | vert |
| d | bleu |
| e | orange |
| f | jaune |
Dans cette configuration initiale on a donc :
xabc = coin "blanc-rouge-vert" xfcb = coin "jaune-vert-rouge"
xadb = coin "blanc-bleu-rouge" xdae = coin "bleu-blanc-orange"
Ouvrir la fenêtre "Console", selectionner "Cube 3" et saisir (aba'b')3 puis valider.
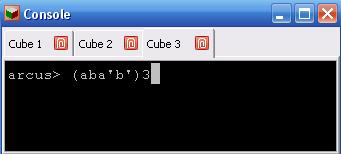
On constate que cette transformation laisse fixe les 8 bords.
- On voit que le coin "blanc-rouge-vert" (qui était en xabc) est devenu le coin xfcb. De plus la face a du coin xabc (blanc) s'est positionnée sur la face f.
- On voit que le coin "jaune-vert-rouge" (qui était en xfcb ) est devenu le coin xabc. De plus la face f du coin xfcb (jaune) s'est positionnée sur la face a.
- On voit que le coin "blanc-bleu-rouge" (qui était en xadb ) est devenu le coin xdae. De plus la face b du coin xadb (rouge) s'est positionnée sur la face e.
- On voit que le coin "bleu-blanc-orange (qui était en xdae ) est devenu le coin xadb.De plus la face e du coin xdae (orange) s'est positionnée sur la face b.
Orientation des coins
Dans le Lemme 10 (Encart 4) il est dit que " ede−1d−1e laisse fixe xabc, xfcb et xadb, et fait tourner xdae d’un tiers de tour".
De nouveau testons cela à partir du Rubik résolu. Pour cela ouvrir un nouveau cube (Cube 4) dans la première fenêtre intitulée "Arcus", en selectionnant "File", puis "New Instance". Puis sélectionner "Cube 4" et appuyer sur la barre d'espace pour faire apparaître les noms des faces.
De nouveau les couleurs des faces dans la configuration initiale sont :
| a | blanc |
| b | rouge |
| c | vert |
| d | bleu |
| e | orange |
| f | jaune |
Dans cette configuration initiale on a donc :
xabc = coin "blanc-rouge-vert" xfcb = coin "jaune-vert-rouge"
xadb = coin "blanc-bleu-rouge" xdae = coin "bleu-gris-orange"
Ouvrir la fenêtre "Console", selectionner "Cube 4" et saisir ed'e'de, puis valider.
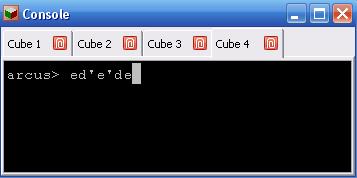
- On constate que cette transformation fixe les coins qui sont en xabc, xfcb et xadb.
- Le coin "bleu-gris-orange" reste en xdae mais tourne d'un tiers de tour (dans le sens des aiguilles d'une montre) amenant la face a (blanc) sur la face e.