Inverses et division
Christine Proust, Equipe REHSEIS
Dans cette fiche, vous trouverez la copie d'une table d'inverses provenant d'une école de Nippur, des explications au sujet de la définition des inverses selon les scribes, et enfin quelques questions pour vous aider à traduire et à comprendre cette tablette scolaire.
Table d'inverses
La figure suivante est la copie d'une table d'inverses trouvée à Nippur et datant de la fin du troisième millénaire, sous le règne des derniers rois sumériens, époque appelée par les historiens "néo-sumérienne". C'est une des plus anciennes tablettes connues contenant des nombres sexagésimaux positionnels.
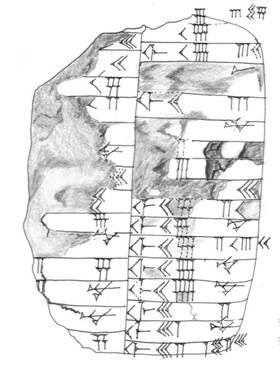
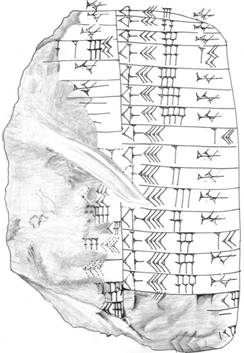
La transcription de cette tablette est donnée ci-dessous. Attention: sur la tablette, les colonnes du revers se succèdent de droite à gauche ; sur la transcription, elles se succèdent dans l’ordre habituel de gauche à droite.
Signes et vocabulaire:
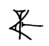igi inverse
nu négation
face, colonne I |
face, colonne II |
igi 2 30
igi 3 20
igi 4 15
igi 5 12
igi 6 10
igi 7 nu
igi 8 7.30
igi 9 6.40
igi 10 6
igi 11 nu
igi 12 5
igi 13 nu
igi 14 nu
igi 15 4
|
igi 16 3.45
igi 17 nu
igi 18 3.20
igi 19 nu
igi 20 3
igi 21 nu
igi 22 nu
igi 23 nu
igi 24 2.30
igi 25 2.24
igi 26 nu
igi 27 2.13.20
igi 28 nu
igi 29 nu
igi 30 2
igi 31 nu
|
revers, colonne III |
revers, colonne IV |
igi 33 nu
igi 34 nu
igi 35 nu
igi 36 1.40
igi 37 nu
igi 38 nu
igi 39 nu
igi 40 1.30
igi 41 nu
igi 42 nu
igi 43 nu
igi 44 nu
igi 45 1.20
igi 46 nu
igi 47 nu
igi 48 1.15
igi 49 nu
igi 50 1.12
|
igi 51 nu
igi 52 nu
igi 53 nu
igi 54 1.6.40
igi 55 nu
igi 56 nu
igi 57 nu
igi 58 nu
igi 59 nu
igi 1 1
igi 1.4 56.15
igi 1.12 50
igi 1.15 48
igi 1.20 45
igi 1.21 44.26.40
igi 1.30 40
igi 1.36 37.30
igi 1.40 36 |
Définition des inverses
Deux nombres forment une paire d’inverses si leur produit est 1 (ou toute autre puissance de 60, positive ou négative).
Exemples :
- 30 est l’inverse de 2 car 2×30 = 1 (pour fixer les idées, on peut penser à une situation familière: 1/2 heure, c’est 30 minutes)
- 15 est l’inverse de 4 car 4×15 = 1
- 7.30 est l’inverse de 8 car 8×7.30 = 1
- 44.26.40 est l’inverse de 1.21 car 1.21×44.26.40 = 1
Nombre régulier
Si vous observez la table d'inverses dont la copie est donnée au début de cette fiche, vous constatez que, pour les scribes, certains nombres ont un inverse (par exemple, l'inverse de 6 est 10), d'autres n'en ont pas (par exemple, 7 n'a pas d'inverse). A quelle condition un nombre possède-t-il un inverse? Plus exactement, à quelle condition un nombre possède-t-il un inverse qui peut s'écrire en base 60 avec une suite finie de chiffres? Des nombres qui possèdent un inverse dont l'écriture sexagésimale est finie sont appelés réguliers en base 60.
Prenons l'exemple qui nous est familier du calcul en base 10.
5 est régulier en base 10 car l'inverse de 5 est 0,2. Mais 3 n'est pas régulier en base 10, car l'inverse de 3 est 0,333333... (suite infinie de chiffres).
Exercice: Quels sont les nombres entiers réguliers en base 10 compris entre 1 et 10? A quelle condition un nombre entier est-il régulier en base 10?
Les nombres réguliers en base 60 sont ceux qui n'ont pas d'autre diviseur premier que 2, 3 et 5.
Exercice: pourquoi? Quels sont les nombres à un chiffre réguliers en base 60?
La division
Exemple: dans la résolution d'un problème, un scribe veut diviser 1.40 par 7.12. Voici comment il procède:
"L'inverse de 7.12 tu extrais: 8.20 il te vient. 8.20 et 1.40 tu multiplies. 13.53.20 il te vient."
Pour diviser 1.40 par 7.12, il multiplie 1.40 par l'inverse de 7.12, qui est 8.20. Le résultat est 13.53.20.
Règle des scribes: diviser un nombre n par un nombre m (régulier en base 60), c’est multiplier n par l’inverse de m.
Exemples
- Pour diviser 50 par 30, on multiplie 50 par 2 car l'inverse de 30 est 2.
50 ÷ 30 = 50 × 2 = 1.40
- Pour diviser 1.40 par 7.30, on multiplie 1.40 par 8 car l'inverse de 7.30 est 8.
1.40 ÷ 7.30 = 1.40 × 8 = 13.20
Exercices
1- Diviser 1.40 par 7.12 (voir exemple cité ci-dessus)
2- Diviser 2.5 par 5
3- Diviser 2.13.20 par 3.20
retour au SOMMAIRE