Dossier de Bernard Vitrac sur les géomètres de la Grèce antique - Chapitre 7 : Archimède
Encart 2 : Exemple de preuve par exhaustion (Archimède, Mesure du cercle)
Pour voir comment la
méthode fonctionne nous nous inspirerons librement de la
première Proposition de la Mesure
du cercle d'Archimède.
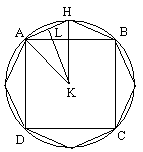
On a un cercle de centre
K, de
rayon AK.
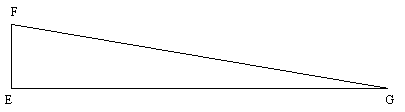
Le triangle rectangle EFG est tel que : EF = AK et la droite EG est égale à la circonférence du cercle.
Nous supposons d'abord
qu'il est
plus grand que EFG. Appelons D la différence d'aire entre le
cercle et EFG.
On inscrit un
carré dans
le cercle, soit ABCD. La différence entre le cercle et le
carré est constituée de quatre segment
égaux, tel AHB. On coupe l'arc AB en deux parties
égales au point H et l'on joint AH, HB. En faisant de
même dans les autres segments, on a donc inscrit un octogone
dans le cercle. Comme le triangle AHB est plus grand que la
moitié du segment de cercle AHB, on en déduit que
la différence entre le cercle et l'octogone,
composée de huit petits segments, est plus petite que la
moitié de la différence qu'il y avait entre le
cercle et le carré. D'après le principe de
continuité (Euclide, X. 1), si l'on
répète la même opération de
dichotomie des arcs, nous construirons un polygone régulier
P, inscrit dans le cercle, tel que la différence d'aire
entre le cercle et lui soit aussi petite que l'on veut. Supposons que
nous la rendions plus petite que la différence D. Nous avons
donc : cercle — EFG > cercle — P. Donc
l'aire du polygone P s'intercale entre celle du triangle EFG et celle
du cercle : EFG <
P < cercle.
Pour simplifier
l'exposé
supposons que ce soit notre octogone qui vérifie cette
inégalité (le raisonnement serait le
même sinon). Cet octogone se décompose en (huit)
triangles isocèles égaux, de même
hauteur et dont les bases, additionnées, constituent le
périmètre de l'octogone. L'aire de notre octogone
est donc égale à un triangle rectangle dont l'un
des côtés de l'angle droit est égal
à la hauteur KL et l'autre est égal au
périmètre de l'octogone.
Mais la hauteur KL est
plus petite
que le rayon AK et le périmètre de l'octogone (ou
de tout autre polygone inscrit) est plus petit que la
circonférence du cercle. Donc le triangle rectangle
égal à notre octogone est plus petit que EFG
puisque chacun des côtés de l'angle droit de l'un
est plus petit que le côté de l'autre qui lui
correspond. Donc l'octogone est plus petit que EFG. Mais, par
construction, il était plus grand. C'est impossible.
On peut raisonner de la même manière si l'on suppose que le cercle est plus petit que EFG. On introduira des polygones réguliers cette fois circonscrits, avec un nombre de côtés suffisant pour obtenir un polygone P' vérifiant la double inégalité : cercle < P' < EFG. On montrera qu'on a aussi P' > EFG ce qui est impossible.
Un
moderne raisonnerait sans doute
autrement ; la formule S = (1/2).(P x h) vaut pour n'importe quel
polygone inscrit dans un cercle, S désignant sa surface, P
son périmètre et h sa hauteur. Si l'on augmente
indéfiniment le nombre de côtés, le
polygone se rapproche du cercle et, à la limite, son
périmètre coïncidera avec la
circonférence du cercle, sa hauteur sera égale au
rayon du cercle. D'où le résultat.