urnes-aleatoires-series-generatrices

Le but de cet article est de présenter un objet étudié en probabilités : les urnes aléatoires. Une urne aléatoire est une boite opaque, contentant des boules de deux couleurs, disons rouge et bleu. Sur la boite on a inscrit une règle d'évolution, sous la forme suivante :

- Tirer une boule au hasard.
- Regarder sa couleur et la remettre dans l'urne.
- Si la boule est rouge, ajouter α boules rouges (α pouvant être négatif, dans ce cas on retirera des boules rouges) et β boules bleues.
- Si la boule est bleue, ajouter γ boules rouges et δ boules bleues (là encore, δ peut être positif ou négatif).
- Recommencer à la première étape

α, β, γ et δ sont des entiers fixés, et on suppose qu'avant le premier tirage, le nombre de boules de chaque couleur présentes dans la boite est connu. On cherche alors comment la composition de cette urne évoluera au fil des tirages. Le nombre de boules présentes dans l'urne après n tirages forme deux suites de variables aléatoires que l'on appelle une chaîne de Markov, c'est-à-dire que seule la valeur de la suite à l'instant n influe sur la loi de la (n+1)^ième variable aléatoire. Insistons sur le fait que dans notre règle d'évolution, on a supposé que la boule tirée est remise dans l'urne.

Un des intérêts des urnes aléatoires est qu'elles donnent des modèles, simples à comprendre et à utiliser, pour simuler des phénomènes divers, en physique, en biologie... On peut par exemple s'intéresser à l'évolution d'un gaz dans deux chambres reliées l'une à l'autre par un trou, pour savoir s'il est possible que tout le gaz rentre dans la première chambre. C'est dans ce but qu'Ehrenfest a introduit l'urne qui porte son nom, afin de démontrer certains paradoxes de la thermodynamique qui annonçait qu'une telle évolution était impossible, le gaz devant forcément s'équilibrer entre les deux chambres. L'urne évolue ainsi : lorsqu'on tire une boule d'une couleur, on la remplace par une boule de l'autre couleur. Le lien avec le modèle est le suivant. On suppose que l'écoulement dans les chambres se fait une molécule après l'autre. Les boules rouges représentent les molécules présentes dans la chambre de gauche, et les bleues celles de la chambre de droite. A chaque étape, une molécule au hasard parmi toutes les molécules présentes change de chambre. On retrouve bien le problème d'Ehrenfest.

Nous pouvons également citer la modélisation d'évolutions de populations. Des modèles déterministes, comme la suite de Fibonacci, que nous expliciterons en Section 2.3. sont connus depuis bien longtemps. Les urnes aléatoires permettent d'obtenir d'autres types de modèles, aléatoires, comme l'urne de Pólya que nous présenterons en Section 3.2, qui permet par exemple de modéliser l'évolution d'une population dans laquelle deux versions d'un même gène coéxistent. Pour cette urne, les boules rouges représentent alors des individus possédant l'une des versions de ce gène, et les boules bleues ceux possédantl'autre version. La boule que l'on tire est alors considérée comme un descendant possédant l'une des deux versions du gène. On ajoute donc dans l'urne une boule de la même couleur que celle que nous avons piochée, et remise.

Afin de calculer la probabilité pour qu'après n étapes, il y ait un certain nombre de boules rouges dans l'urne, nous aurons besoin d'une notion très utile en combinatoire, celle de série génératrice. L'idée est d'associer une fonction à une suite, de telle sorte que des égalités sur les quantités de la suite (comme des formules de récurrence) se transforment en équations fonctionnelles (équation différentielle, équation du second degré, etc.). On utilise alors des résultats d'analyse afin de déterminer cette fonction, pour ainsi remonter à la suite inconnue.

D'une certaine manière, la série génératrice (la fonction associée) "retient" toute l'information contenue dans la suite, y compris pour les très grandes valeurs, alors qu'en combinatoire, la plupart des raisonnements se font à entier n fixé. Cette "connaissance" des grandes valeurs nous permet alors d'appliquer les relations connues à toute la suite à la fois, et donc d'obtenir une information supplémentaire. De plus les outils d'analyse permettent une écriture très simple de certaines relations compliquées.

Nous commencerons par présenter les séries génératrices, que nous appliquerons tout d'abord au calcul de la fameuse suite de Fibonacci. Ensuite nous reviendrons aux urnes aléatoires en général, avant d'appliquer les résultats présentés au cas de l'urne de Pólya.

2. Série génératrice

Présentons maintenant ce qu'est une série génératrice. On a déjà expliqué qu'il s'agissait d'une fonction associée à une suite permettant notamment deux opérations : connaissant la fonction, on doit pouvoir retrouver la suite, et les relations connues sur les suites doivent pouvoir se traduire sur la fonction. Nous définissons la série génératrice associée à la suite $(a_n)_{n \in N}$ comme :

$\displaystyle{f : z \in C \mapsto a_0+a_1z+a_2z^2+....}$

Cette fonction est bien définie pour $z$ assez petit, pourvu que $(a_n)_{n\in N}$ ne croisse pas trop vite. Par exemple, si $a_n\leq A^n$ pour tout $n$, la limite de $\left(\sum_{k=0}^n a_k z^k\right)_{n\in N}$ existe pour tout $|z| < \frac{1}{A}$. Donc dans ce cas, la série génératrice est bien définie, et on peut calculer avec.

2.1 Propriétés des séries génératrices

Nous devons pour commencer vérifier que les séries génératrices caractérisent les suites auxquelles elles sont associées de manière non équivoque, c'est-à-dire que si deux séries génératrices sont égales, alors les suites associées le sont aussi.

Prenons deux suites $(a_n)_{n\in N}$ et $(b_n)_{n\in N}$. Si nous avons :

$a_0+a_1z+a_2z^2+... = b_0+b_1z+b_2z^2+...$
alors pour $z=0$ nous avons $a_0=b_0$. Soustrayons $a_0=b_0$, et divisons par $z$ nous avons :

$a_1 + a_2 z + a_3 z^2 + ... = b_1 + b_2 z + b_3 z^2 + ...$
Ce qui nous permet de voir que $a_1=b_1$, en faisant tendre $z$ vers 0. En réitérant le processus nous obtenons bien que les suites $(a_n)_{n \in N}$ et $(b_n)_{n\in N}$ sont identiques.

Par conséquent, à chaque fonction est associée au plus une série génératrice, mais cette preuve nous donne davantage : connaissant une fonction qui est une série génératrice, nous pouvons calculer la suite de termes associée en utilisant la méthode précédente. Par exemple, pour $\displaystyle{f(z) = \frac{1}{1+z^2}}$, nous avons :

$\begin{eqnarray} a_0 & = & f(0) = 1\\ a_1 & = & \lim_{z \to 0} \frac{1}{z}(f(z)-a_0) = lim_{z \to 0} \frac{-z}{1+z^2} = 0\\ a_2 & = & \lim_{z \to 0} \frac{1}{z}\left(\frac{-z}{1+z^2}-0\right) = \lim_{z\to 0} \frac{-1}{1+z^2} = -1\\ a_3 & = & \lim_{z \to 0} \frac{1}{z}\left( \frac{-1}{1+z^2} + 1 \right) = \lim_{z\to 0} \frac{z}{1+z^2} = 0\\ \cdots \end{eqnarray}$

Nous pourrions bien sûr itérer ce processus pour obtenir pour tout entier n :

$\displaystyle{a_n = \lim_{z \to 0} \frac{1}{z^n}[f(z) - (a_0+a_1z+a_2z^2+... + a_{n-1} z^{n-1})]}$
mais cette formule nous demande de calculer tous les termes jusqu'au rang n - 1 pour connaître le n^ième terme, alors que nous souhaiterions connaître une formule valable quel que soit l'entier n. Notons que $(a_n)_{n \in N}$ ne dépend que des valeurs de $f$ pour $z$ proche de 0. On pourra par conséquent toujours supposer que $z$ est assez petit, et restreindre $f$ à une fonction définie sur un voisinage de 0.

Une autre propriété intéressante de ces séries est leur comportement intuitif vis-à-vis des opérations usuelles. Notamment, si l'on pose :

$\displaystyle{f(z) = a_0+a_1z+a_2z^2+...$ et $g(z) = b_0+b_1z+b_2z^2+...}$,
on a alors (pour des $z$ assez petits) :
$\displaystyle{f'(z) = a_1 + 2 a_2 z + 3 a_3 z^2 + ...}$
$\displaystyle{f(z) + g(z) = (a_0 + b_0) + (a_1+b_1)z + (a_2+b_2)z^2 + ...}$

$\begin{eqnarray} f(z)g(z) & = & (a_0+a_1z+a_2z^2+...)(b_0+b_1z+b_2z^2+...)\\ & = & a_0b_0 + (a_1b_0 + a_0b_1) z + (a_2b_0 + a_1b_1 + a_0b_2)z^2 + \cdots \end{eqnarray}$

Par conséquent, $f'$ est la série génératrice associée à la suite $((n+1)a_{n+1})_{n \in N}$, $f+g$ est celle associée à $(a_n+b_n)_{n \in N}$, et $fg$ à $(\sum_{k=0}^n a_kb_{n-k})_{n \in N}$.

Intéressons-nous maintenant à la détermination de séries génératrices remarquables, qui nous permettrons de calculer par la suite les développements des fonctions que nous obtiendrons.

2.2 Calcul des coefficients de fonctions "utiles"

Les séries génératrices que nous aurons à développer par la suite pourront être exprimées comme somme de fonctions plus simples de la forme $\displaystyle{z \to \frac{1}{(1-z)^i}}$. Par conséquent nous allons déterminer quelles sont les suites associées à ces fonctions. Nous commençons par calculer le développement de $\displaystyle{z \to \frac{1}{1-z}}$.

Soit $g_n$ la fonction définie (pour $|z|<1$) comme suit :

$g_n(z) = 1 + z + z^2 + ... + z^n.$
On remarque que
$zg_n(z)-g_n(z) = z + z^2 + ... + z^{n+1} - (1 + z + ... + z^n )= z^{n+1}-1$.
Par conséquent $\displaystyle{g_n(z) = \frac{z^{n+1}-1}{z-1}}$. En faisant tendre $n$ vers $+\infty$, nous obtenons alors :
$\displaystyle{\lim_{n \to +\infty}g_n(z) = \frac{1}{1-z}}$
Ce qui nous donne en définitive l'égalité suivante valable pour $|z|<1$ :
$\displaystyle{1 + z + z^2 + ... = \frac{1}{1-z}}$
autrement dit, la suite associée à la fonction $\displaystyle{z \mapsto \frac{1}{1-z}}$ est la suite constante égale à 1.

Dès lors nous pouvons écrire, pour $a,b,c \in R$ :

$\displaystyle{\frac{a}{bz+c} = \frac{a}{c} \frac{1}{1-\left(-\frac{bz}{c}\right)} = \frac{a}{c}\left(1 -\frac{b}{c} z + \frac{b^2}{c^2}z^2 + ...\right)}$,
donc par conséquent le $n^{ième}$ coefficient associé à cette fonction s'écrira $\displaystyle{a\frac{(-b)^n}{c^{n+1}}}$.

Nous allons généraliser un peu plus notre propos, et développer $\displaystyle{f_p : z \to \frac{1}{(1-z)^p}.}$

Pour cela procédons par récurrence. On sait que pour $p=1$, tous les coefficients sont égaux à 1. Pour $p=2$, remarquons que $f_2 = f_1'$. Par conséquent, il suffit de dériver l'écriture de $f_1$ en série génératrice pour obtenir :

$f_2(z) = 1 + 2 z + 3 z^2 + ...$
De manière générale, on remarque que $\displaystylef_{p+1} = \frac{1}{p}f_p'}$. On obtient ainsi par récurrence que, pour tout $n \in N$ :
$\displaystyle{f_p(z) = 1 + \left(\begin{array}{ c }p \\1 \end{array} \right) z +\left(\begin{array}{ c }p+1 \\2 \end{array} \right) z^2 + \left(\begin{array}{ c }p+2 \\3 \end{array} \right)z^3+ ...}$
Soit par conséquent, le $n^{ième}$ coefficient associé à $f_p$ est égal à
$\displaystyle{\left(\begin{array}{ c }n+p-1 \\n \end{array} \right)= \left(\begin{array}{ c }n+p-1 \\p-1 \end{array} \right)}$.
Nous allons maintenant appliquer ces résultats une première fois à la suite de Fibonacci.

2.3 La suite de Fibonacci

2.3.1 Génération de la suite

La suite de Fibonacci a été introduite au XIII^e siècle par Leonardo Fibonacci. Cette suite peut représenter, par exemple, l'évolution d'une population de lapins qui se reproduisent de la manière suivante. Un jeune couple de lapins met un mois à devenir adulte, et tout couple de lapins adultes donne naissance à un nouveau couple chaque mois. On note $f_n$ le nombre de couples de lapins présents au début du $n^{ième}$ mois, et on suppose qu'au premier mois, on ne possède qu'un unique couple de jeunes lapins.

Nous commençons par déterminer la formule de récurrence. Le nombre de couples de lapins naissant le $(n+2)^{ième}$ mois est égal au nombre de couples âgés de plus d'un mois présents. Or il y a $f_{n+1}-f_n$ couples qui sont nés au $(n+1)^{ième}$ mois qui sont donc des jeunes qui ne se reproduisent pas. Chacun des $f_n$ couples âgés d'au moins un mois donne alors naissance à un nouveau couple. On a en définitive :

$\displaystyle{f_{n+2}=2f_n + (f_{n+1}-f_n) = f_{n+1}+f_n.}$
Les conditions initiales sont données par $f_0=0$ et $f_1=1$.

Cette suite est très connue en raison de son lien avec le nombre d'or $\displaystyle{\Phi= \frac{1+\sqrt{5}}{2}}$. En particulier on remarque que le rapport $\displaystyle{\frac{f_{n+1}}{f_n}}$ tend vers $\Phi$ quand $n$ tend vers l'infini, comme nous le montrerons ci-dessous.

2.3.2 Construction et calcul de la série génératrice

Soit $\psi$ la série génératrice associée à la suite de Fibonacci, qui est définie par :

$\displaystyle{\psi(z)=f_0+f_1z+f_2z^2+...}$

Nous utilisons alors la relation de récurrence pour calculer explicitement $\psi$. En effet, en écrivant $f_{n+2} = f_{n+1}+f_n$ dans la formule précédente, nous obtenons :

$\begin{eqnarray} \psi(z) & = & f_0+f_1z+f_2z^2+...\\ & = & f_0 + f_1z + \left( f_2 z^2 + f_3z^3+f_4 z^4 + \cdots\right)\\ & = & z + \left( (f_0+f_1) z^2 + (f_1+f_2)z^3+(f_2+f_3) z^4 + \cdots\right)\\ & = & z + z^2\left(f_0+f_1z+f_2z^2+...\right) + z \left( f_0+f_1z+f_2z^2+... \right)\\ & = & z + z\psi(z) + z^2\psi(z). \end{eqnarray}$

On vient d'appliquer à la série génératrice la relation de récurrence que nous connaissions pour la suite. Cela se traduit par une égalité fonctionnelle, particulièrement simple dans ce cas particulier, qui nous permet de déterminer $\psi$ :

$\displaystyle{\psi(z) = \frac{z}{1-z-z^2}.}$

Ce n'est malheureusement pas une forme que l'on sait facilement développer en série entière. Nous allons donc la décomposer en éléments simples. Commençons par déterminer les solutions de $z^2+z-1=0$. On obtient $\displaystyle{\omega_1=\frac{\sqrt{5}-1}{2}= \frac{1}{\Phi}}$ et $\displaystyle{\omega_2 = -\frac{1+\sqrt{5}}{2}=-\Phi$, où on a posé $\displaystyle{\Phi= \frac{1+\sqrt{5}}{2}}}$ le nombre d'or. On écrit alors :

$\displaystyle{\psi(z) = \frac{a}{\omega_1-z} + \frac{b}{\omega_2-z}.}$
En réduisant au même dénominateur il vient :
$\displaystyle{\psi(z) = \frac{-(a+b)z + \left(-a\Phi+\frac{b}{\Phi}\right)}{z^2+z-1} = \frac{-z}{z^2+z-1}}$,
d'où on tire le système :
$\displaystyle{ \left\{ \begin{array}{rcl} a + b & = & 1\\ \frac{b}{\Phi}- a \Phi & = & 0 \end{array} \right.}$
soit $\displaystyle{a=\frac{1}{1+\Phi^2}}$ et $\displaystyle{b=\frac{\Phi^2}{1+\Phi^2}}$.

En utilisant les calculs du paragraphe précédent et en déterminant la série génératrice associée à $\psi$, nous obtenons alors pour $f_n$ :

$\begin{eqnarray} f_n & = & a \frac{1}{\omega_1^{n+1}} + b \frac{1}{\omega_2^{n+1}}\\ & = & \frac{1}{1+\Phi^2} \left( \Phi^{n+1} + \frac{(-1)^{n+1}}{\Phi^{n-1}} \right) \end{eqnarray}$

On en déduit une expression explicite pour la suite de Fibonacci ne nécessitant pas le calcul des $n$ premiers termes pour donner $f_{n+1}$. En particulier, on obtient bien, grâce à un petit calcul, que $\displaystyle{lim_{n \to +\infty}\frac{f_{n+1}}{f_n} = \Phi}$.

3. Urne aléatoire

Les urnes aléatoires ont été introduites il y a plus de trois siècles, et les premiers résultats ont été démontrés par Jacob Bernouilli et Laplace [Flajolet, Dumas et Puyhaubert, 2006]. Par la suite de nombreuses urnes particulières ont été introduites pour modéliser certains problèmes, parmi lequelles les urnes d'Ehrenfest, Friedman ou encore Pólya sont certainement les plus connues. Nous allons maintenant utiliser les outils que nous venons de développer pour étudier l'urne de Pólya. Comme l'approche que nous avons choisi s'étend sans grandes difficultés à de très nombreux types d'urnes, nous nous placerons pour commencer dans un cadre général. Nous laissons à la curiosité du lecteur l'application des résultats obtenus ici à d'autres urnes aléatoires, comme l'urne d'Ehrenfest, ou bien d'autres [1].

3.1 Série génératrice associée à l'urne aléatoire

Commençons par nous intéresser à une urne aléatoire générale. Rappelons que la règle est la suivante : si on a tiré une boule rouge, on ajoute $\alpha$ boules rouges et $\beta$ bleues à l'urne, et si on a tiré une boule bleue, on en ajoute $\gamma$ rouges et $\delta$ bleues. On note $a_0$ et $b_0$ le nombre (déterministe) de boules respectivement rouges et bleues présentent à l'instant 0, et $a_n$ et $b_n$ le nombre (aléatoire) de boules de chaque couleur présentes dans l'urne après $n$ étapes.

Nous cherchons quelle est la probabilité pour une urne donnée d'arriver après $n$ étapes à une configuration avec $a$ boules rouges et $b$ boules bleues. Pour cela nous avons besoin de déterminer le nombre d'"histoires" possibles pour l'urne conduisant à une configuration avec $a$ boules rouges et $b$ boules bleues en $n$ étapes. Une "histoire" est donnée par la suite des boules tirées, chacune étant supposées distinctes. Par exemple, pour l'urne de Pólya partant d'une boule rouge et d'une boule bleue, il existe deux histoires menant à deux boules rouges et deux boules bleues après deux étapes : celle où on a d'abord tiré la boule rouge et celle où on a d'abord tiré la boule bleue. Il existe également deux histoires menant à trois boules rouges et une bleue selon la boule rouge tirée à la deuxième étape, l'"ancienne" ou la "nouvelle".

Figure I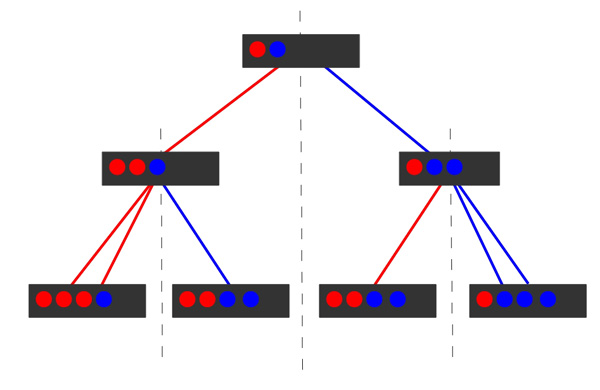

Arbre des "histoires" d'une urne de Pólya

La figure I montre que pour l'urne de Pólya, après 2 étapes, chacune des compositions possibles est donnée par deux histoires. On remarquera que l'on distingue bien dans la deuxième étape le choix de la première boule rouge et celui de la deuxième dans la partie gauche du tableau, et de même dans la partie droite pour ce qui est des boules bleues.

Toutes les histoires possibles de longueur $n$ sont équiprobables. Par conséquent, si on note $h_n(a,b)$ le nombre d'histoires de longueur $n$ menant à une urne composée de $a$ boules rouges et $b$ boules bleues et $h_n$ le nombre total d'histoires de longueur $n$, alors on a :

$\displaystyle{P(a_n=a,b_n=b) = \frac{h_n(a,b)}{h_n}.}$

Nous allons calculer $h_n(a,b)$ grâce à la notion de série génératrice. Comme la quantité $h_n(a,b)$ croit très vite quand $n$ croit, nous allons utiliser une série génératrice exponentielle, associée à $\displaystyle{\frac{h_n(a,b)}{n!}}$, où $n!=1\times \cdots \times n$, qui croira donc à un rythme bien plus acceptable.

Il y a néanmoins un autre problème, nous avons trois quantités à retenir simultanément : le nombre de boules rouges, le nombre de boules bleues, et le nombre d'étapes que nous avons effectué. Néanmoins, après $n$ étapes, l'urne ne peut être que dans un nombre fini d'états différents, par conséquent, la somme suivantea :

$\sum_{a,b} h_n(a,b) x^a y^b$
est finie quel que soit l'entier $n$. C'est un polynôme en deux variables $x$ et $y$. Si $x$ et $y$ sont maintenant pensés comme des paramètres, la connaissance de cette quantité (dépendant de $n$) pour tout couple $(x,y)$ nous permettra de remonter au polynôme puis aux coefficients. Étudions donc la série génératrice exponentielle associée à ces quantités : $\displaystyle{H_{x,y}(z) = \left(\sum_{a,b} h_0(a,b) x^ay^b\right) + \left(\sum_{a,b} h_1(a,b) x^ay^b \right)\frac{z}{1} + \left(\sum_{a,b} h_2(a,b) x^ay^b\right) \frac{z^2}{2} + \cdots.}$

Ceci nous permet donc d'introduire la série génératrice exponentielle associée à l'urne comme la fonction de trois variables $x,y,z$ suivante :

$H : (x,y,z) \mapsto H_{x,y} (z)$.

Comme nous l'avons vu précédemment, connaître cette fonction nous permet de remonter aux coefficients, en considérant tout d'abord $(x,y)$ comme des paramètres de notre fonction de la variable $z$.

Pour $x=y=1$, la fonction $z \mapsto H(1,1,z)$ est intéressante en elle-même. En effet, $h_n$ est la somme des $h_n(a,b)$ pour tous les couples $(a,b)$ possibles (le nombre d'histoires de longueur $n$ est bien égal à la somme sur tous les états possibles du nombre d'histoires de longueur $n$ menant à un état donné). Par conséquent, comme $H(1,1,z)$ est la somme de tous les termes $\displaystyle{h_n(a,b)\frac{z^n}{n!}}$, pour $a,b,n$ entiers, en commençant par faire les sommes par rapport à $a$ et $b$ à entier $n$ fixé, on obtient que $H(1,1,z)$ s'écrit comme la somme des $\displaystyle{h_n \frac{z^n}{n!}}$. Autrement dit, nous venons de prouver que la fonction $z \mapsto H(1,1,z)$ est la série génératrice exponentielle associée à la suite $(h_n)$.

Afin d'établir une égalité fonctionnelle pour $H$, il va nous falloir utiliser une représentation astucieuse de notre urne aléatoire, utilisant des équations aux dérivées partielles.

3.1.1 Représentation d'une urne aléatoire par une dérivation

Nous pouvons remarquer que dans la série génératrice précédente, une urne avec $a$ boules rouges et $b$ boules bleues est représentée par le monôme $x^ay^b$. Or si on définit les fonctions suivantes :

$u : x,y \mapsto x$

$v : x,y \mapsto y$,
on a $x^ay^b = u^a(x,y)v^b(x,y)$. On dit alors que l'urne contenant $a$ boules rouges et $b$ boules bleues est codée par la fonction $u^av^b$.

Lorsqu'on réalise un tirage de cette urne, on crée $a$ histoires pour lesquelles on a tiré une boule rouge et $b$ pour lesquelles c'est une boule bleue qui est tirée. Par conséquent, à une fonction $u^av^b$, on associe $a$ fonctions $u^{a+\alpha}v^{b+\beta}$ et $b$ fonctions $u^{a+\gamma}v^{b+\delta}$. Cela revient à appliquer l'opérateur aux dérivées partielles suivant à notre fonction :

$D = u^{\alpha+1}v^\beta \partial_x + u^\gamma v^{\delta+1}\partial_y.$

En effet on a $D(u^av^b) = a u^{a+\alpha}v^{b+\beta} + b u^{a+\gamma}v^{b+\delta}.$ Par conséquent l'évolution de l'urne est gouvernée par cet opérateur, que l'on associe à l'urne. On peut se servir de celui-ci pour réécrire la série génératrice associée à l'urne.

3.1.2 Système différentiel associé à l'urne

La série génératrice que nous cherchons est obtenue en itérant la dérivation associée à l'urne. Supposons que nous commencions avec $a_0$ boules rouges et $b_0$ boules bleues. L'état est représenté par $u^{a_0}v^{b_0}$. Les états accessibles après une étape, (comptés avec le nombre de manières possibles pour arriver à chacun d'entre eux) sont représentés par $D(u^{a_0}v^{b_0})$. Après deux étapes, c'est $D(D(u^{a_0}v^{b_0}))= D^2(u^{a_0}v^{b_0})$ qui code la somme des états accessibles, puis $D^3(u^{a_0}v^{b_0})$ après trois étapes, etc...

On peut alors réécrire la série génératrice en regroupant tous les termes associés à $z^n$. Grâce à l'opérateur $D$, nous pouvons alors écrire :

$H(x,y,z) = (u^{a_0}v^{b_0})(x,y) + D(u^{a_0}v^{b_0})(x,y) + \frac{1}{2!}D^2(u^{a_0}v^{b_0})(x,y) + \frac{1}{3!}D^3(u^{a_0}v^{b_0})(x,y)+\cdots$

Ceci nous donne un moyen d'obtenir une équation fonctionnelle satisfaite par $H$. Pour cela, appliquons l'opérateur $D$ à l'égalité ci-dessus.

$\begin{eqnarray} D(H)(u,v,z) & = & \sum_{n=0}^{+\infty} D^{n+1} (u^av^b)\frac{z^n}{n!}\\ & = & \sum_{n=0}^{+\infty} D^{n+1} (u^av^b)\partial_z \frac{z^{n+1}}{(n+1)!}\\ & = & \partial_z \sum_{n=1}^{+\infty} D^n (u^av^b)\frac{z^n}{n!}\\ & = & \partial_z H. \end{eqnarray}$

$H$ vérifie par conséquent l'équation aux dérivées partielles suivante :

$\partial_z H = x^{\alpha+1} y^\beta\partial_x H + x^\gamma y^{\delta+1} \partial_y H.$

Pour résoudre cette équation différentielle on va chercher un couple de fonctions $(X(z), Y(z))$ qui se comportent, lorsqu'on les dérive par rapport à $z$, de la même manière que $u$ et $v$ lorsqu'on leur applique $D$. Autrement dit on veut que, pour tout choix de $(a,b) \in N$, on ait :

$(X^aY^b)'(z) = aX(z)^{a+\alpha}Y(z)^{b+\beta}+bX(z)^{a+\gamma}Y(z)^{b+\delta}.$

Or on sait que :

$(X^aY^b)' = a X^{a-1}X'Y^b + b X^aY^{b-1}Y'.$
Donc en choisissant successivement $a=1,b=0$ et $a=0,b=1$, il vient que $X$ et $Y$ vérifient en particulier le couple d'équations différentielles suivant :
$\displaystyle{ \left\{ \begin{array}{l} \dot{X} = X^{\alpha+1}Y^\beta \\ \dot{Y} = X^\gamma Y^{\delta+1} \end{array} \right.}$

Maintenant, si les équations différentielles suivantes sont vérifiées par un couple de fonctions $(X_x,Y_y)$ satisfaisant la condition initiale $X_x(0)=x,Y_y(0)=y$, alors on a :

$\displaystyle{\partial_z (X_x^aY_y^b)(z) = D(u^av^b)(X(z),Y(z)) = aX(z)^{a+\alpha}Y(z)^{b+\beta}+bX(z)^{a+\gamma}Y(z)^{b+\delta}.}$
Or $H(x,y,z) = \sum_{n=0}^{+\infty} D^n(u^{a_0}v^{b_0})(x,y)\frac{z^n}{n!}$, donc on a :

$\begin{eqnarray} H(x,y,z) & = & \sum_{n=0}^{+\infty} D^n(u^{a_0}v^{b_0})(X_x(0),Y_y(0))\dfrac{z^n}{n!}\\ & = & \sum_{n=0}^{+\infty} \partial_z (X_x^{a_0} Y_y^{b_0})(0) \frac{z^n}{n!}\\ & = & (X_x(z)^{a_0}Y_y(z)^{b_0}) \end{eqnarray}$

Nous venons d'obtenir une méthode générale permettant de calculer les valeurs de $h_n(a,b)$. Grâce à cette formule, si on est capable de résoudre le système d'équations différentielles précédent pour une urne aléatoires, alors on est capable de calculer la probabilité d'arriver dans un état donné en un certain nombre d'étapes. Nous allons maintenant appliquer les résultats obtenus au cas de l'urne de Pólya.

3.2 L'urne de Pólya

Rappelons que l'urne de Pólya permet d'étudier l'évolution d'une population de deux espèces. Elle a été introduite par Pólya [Pólya, 1930] et été étudiée maintes fois par la suite. [Tautu,1986] en donne un bref aperçu historique. L'urne est définie avec les quantités suivantes : $\alpha=1, \beta=0, \gamma = 0$ et $\delta=1$, autrement dit, quand on tire une boule d'une couleur, on en ajoute une de la même couleur. Le système associé à l'urne est alors le suivant :

$\displaystyle{ \left\{ \begin{array}{l} \dot{X} = X^2 \\ \dot{Y} = Y^2 \end{array} \right.}$
qui se résout immédiatement en $\displaystyle{X_x(t)= \frac{x}{1-xt}, Y_y(t) = \frac{y}{1-yt}}$. On a alors :
$\displaystyle{H(x,y,z) = \left(\frac{x}{1-xz}\right)^{a_0}\left(\frac{y}{1-yz}\right)^{b_0}.}$
On peut alors développer $H$ en séries entières pour calculer $h_n(a,b)$. Pour cela nous commencerons par rappeler que :

$\displaystyle{\left(\frac{x}{1-xz}\right)^{a_0} = x + \left(\begin{array}{ c }a_0 \\a_0-1 \end{array} \right)x^2z + \left(\begin{array}{ c }a_0+1 \\a_0-1 \end{array} \right)x^3z^2 + \cdots}$
On doit maintenant réaliser le produit des deux développements suivants pour obtenir le développement en séries génératrices de notre urne. Rappelons que :

$(a_0+a_1z+a_2z^2+...) (b_0+b_1z+b_2z^2+...) = a_0 b_0 + (a_1 b_0 + a_0 b_1) z + (a_2b_0+a_1b_1+a_0b_2)z^2 + \cdots$

En d'autres termes, au produit de deux séries génératrices de coefficients $(a_n)$ et $(b_n)$ est associé la suite $(a_0b_n+a_1b_{n-1} + \cdots + a_nb_0)$. Dans notre cas, la série entière de $z$ $H_{x,y}(z)=H(x,y,z)$ (nous considérons de nouveau $x$ et $y$ comme des paramètres) possède les coefficients suivants :

$\displaystyle{\left(\begin{array}{ c }b_0+n-3 \\b_0-1\end{array} \right) xy^{n+1} + \left(\begin{array}{ c }a_0 \\a_0-1 \end{array} \right) \left(\begin{array}{ c }b_0+n-4 \\b_0-1\end{array} \right) x^2y^n + \cdots + \left(\begin{array}{ c }a_0+n-3\\a_0-1 \end{array} \right)x^{n+1}y.}$
Or rappelons que ces coefficients s'écrivent également (c.f. Section 3.1, la définition de $H(x,y,z)$ :
$\displaystyle{\frac{1}{n!}\left(h_n(0,n+2) y^{n+2} + h_n(1,n+1)xy^{n+1} + \cdots + h_n(n+1,1) x^{n+1}y\right).}$

Ceci nous permet par conséquent de calculer le nombre d'histoires de longueur $n$ menant à un état particulier de l'urne :

$\displaystyle{\frac{h_n(a,b)}{n!} = \left\{ \begin{array}{l} \left(\begin{array}{ c }a-1 \\a_0-1 \end{array} \right)\left(\begin{array}{ c }b-1 \\b_0-1 \end{array} \right) \textrm{ si } a_0 \leq a \leq a_0+n \textrm{ et si } b = n+a_0+b_0-a\\ 0 \textrm{ sinon.}} \end{array} \right.}$
De plus, en se souvenant que la série génératrice exponentielle associée à cette suite est $\displaystyle{H(1,1,z) = \frac{1}{(1-z)^{a_0+b_0}}}$, on obtient l'égalité :
$\displaystyle{\frac{h_n}{n!} = \left(\begin{array}{ c }n+a_0+b_0-1 \\a_0+b_0-1 \end{array} \right).}$

Finalement, toutes les histoires étant équiprobables, si on note $a_n$ le nombre de boules rouges présentes dans l'urne à l'instant $n$ et $b_n$ le nombre de boules bleues présentes à cet instant, nous obtenons les probabilités suivantes, qui nous permettent de déterminer l'évolution de toute urne (on utilisera le fait que le nombre total de boules à l'instant $n$ est connu, $a_n+b_n=a_0+b_0+n$, par conséquent nous pouvons nous intéresser au seul nombre de boules rouges, celui de boules bleues s'en déduit) :

$\displaystyle{P(a_n=a,b_n=n+a_0+b_0-a) = P(a_n=a) = \frac{\left(\begin{array}{ c }a-1 \\a_0-1 \end{array} \right)\left(\begin{array}{ c }n+a_0+b_0-a-1 \\b_0-1 \end{array} \right)}{\left(\begin{array}{ c }n+a_0+b_0-1\\a_0+b_0-1 \end{array} \right)}\textrm{ si } a_0 \leq a \leq a_0+n}$

Nous pouvons maintenant interpréter les résultats obtenus. Commençons par une observation. On remarque que si $a_0=b_0=1$, c'est-à-dire que l'on commence avec une boule rouge et une boule bleue dans l'urne, alors toutes les urnes possibles au temps $n$ ont exactement la même probabilité d'apparaître.

Mais cette propriété n'est pas vraie quel que soit le nombre de boules avec lequel nous débutons : par exemple, si nous étudions une urne dans laquelle il y a au départ deux boules de chaque couleur, soit $a_0=b_0 = 2$, nous obtenons grâce à un calcul rapide :

$\displaystyle{P(a_n=a) = 6\frac{(a-1)(n+3-a)}{(n+3)(n+2)(n+1)}.}$

Ainsi, dans ce cas, on voit clairement que tous les états possibles au temps $n$ ne sont pas équiprobables. En particulier, une urne qui possède une moitié de boules rouges apparaît avec la probabilité $\displaystyle{\frac{3(n+4)^2}{2(n+3)(n+2)(n+1)}}$ à l'étape $n$ alors qu'une urne ne possédant que deux boules rouges à l'étape $n$ n'apparaît qu'avec la probabilité $\displaystyle{\frac{6}{(n+3)(n+2)}}$.

Figure II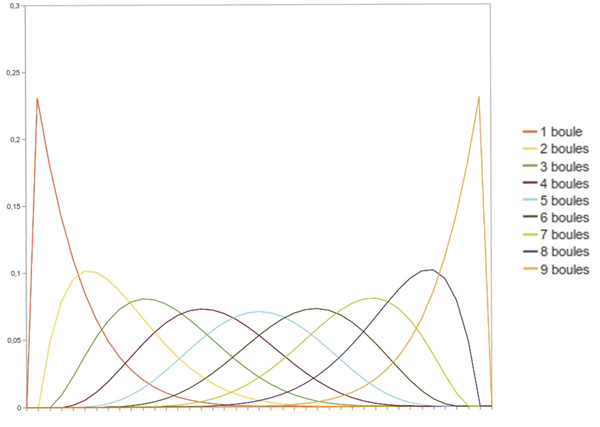

Distribution des probabilités d'apparition d'une urne après 30 tours en fonctions des conditions initiales

Sur la figure II, nous avons représenté la probabilité de posséder $a$ boules rouges pour une urne de Pólya ayant subi 30 étapes d'évolution, à partir de toutes les situations initiales possibles avec 10 boules, de 1 rouges et 9 bleues à 9 rouges et 1 bleues.

Chacune de ces distributions de probabilités est "piquée" au voisinage de la proportion de boules qu'il contient. Autrement dit, une urne de Pólya favorise dans le futur les configurations qui possèdent un nombre moyen de boules voisin du sien.

Ainsi une urne de Pólya commençant avec une proportion $r$ de boules rouges parmi ses boules rend plus probable les compositions d'urnes pour lesquelles cette proportion est conservée. En particulier, si on commence avec $\frac{1}{3}$ de boules rouges dans l'urne, on a de fortes chances que ce rapport soit conservé pour toujours. Ce phénomène s'accentue quand le nombre total de boules augmente, autrement dit, plus le nombre initial de boules est grand, plus il est difficile de modifier le ratio de boules rouges présentes dans l'urne.

Or une urne aléatoire vérifie une propriété remarquable : si à un moment donné nous regardons dans l'urne le nombre de boules de chaque couleur et que nous replaçons ensuite le couvercle, et recommençons à faire évoluer cette urne, alors l'urne se comporte comme si on avait dès le début commencé avec la composition que nous venons de découvrir. Cette propriété s'appelle la propriété de Markov. L'urne évolue à partir du temps $n$ exactement comme si on avait à l'instant intial commencé avec $a_n$ boules rouges et $b_n$ boules bleues.

Revenons à l'urne de Pólya. On vient de voir que si la composition initiale est de une boule rouge et une boule bleue, alors à un instant donné toutes les compositions de l'urne sont équiprobables. Mais alors le ratio de boules rouges dans l'urne est une variable aléatoire choisie uniformément au hasard. Or si on repart ensuite d'un instant donné, ce ratio aura tendance à se conserver ! Par conséquent, le ratio de boules rouges tend vers une constante, mais cette constante est aléatoire de loi uniforme.

Autrement dit, si on trace le graphe représentant l'évolution du nombre de boules rouges présentes dans l'urne au cours du temps, on obtient pour chaque réalisation de l'expérience une courbe proche d'une droite linéaire, mais dont la pente est aléatoire, et varie de telle façon qu'à un temps donné, sa distribution sur l'axe des ordonnées varie selon une loi uniforme (à entier $n$ fixé, les probabilités d'atteindre chacun des points $(n,k)$ pour $1\leq k \leq n+1$ sont égales).

On a représenté sur la figure III l'évolution du nombre de boules rouges de 11 réalisations d'urnes de Pólya, entre les instants 0 et 500. On remarquera l'allure de droite de ces courbes, ainsi que leur caractère uniforme.

Figure III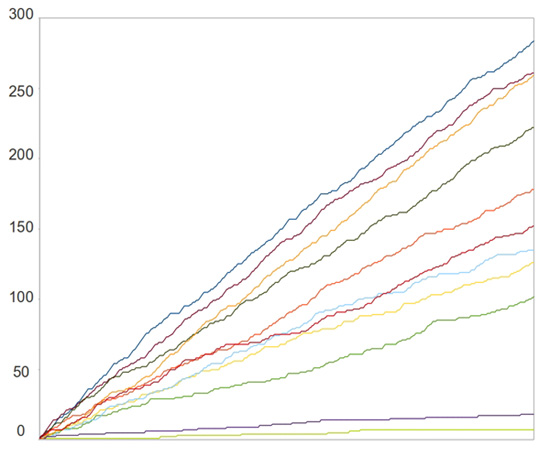

11 réalisations d'urnes de Pólya au cours du temps, partant d'une boule rouge et d'une boule bleue

L'urne de Pólya modélise donc une population autostable, pour laquelle tout équilibre à un instant donné tend à être conservé à l'infini, avec une probabilité d'autant plus grande que le nombre d'individus est grand, cet équilibre restant toutefois aléatoire. Nous pourrions préciser quelle est la probabilité, partant d'une situation donné, que ces populations s'éloigne de manière significative de leur équilibre, c'est ce dont s'occupe la théorie des grandes déviations. De nombreuses autres questions peuvent encore se poser sur le comportement à l'infini de telles urnes.

Conclusion

On a vu dans cet article comment nous pouvions utiliser des séries génératrices pour calculer certaines quantités (suite récurrente d'ordre 2, comme la suite de Fibonacci, probabilité pour une variable aléatoire d'avoir une valeur donnée, nombres d'objets de taille $n$ dans un ensemble...). Le nombre d'application possibles ne s'arrête certainement pas ici. Il y a encore de nombreux cas pour lesquels cette méthode se révèle l'une des plus aisée, comme pour le calcul des nombres de Catalan, qui comptent le nombre d'arbres planaires à $n$ branches (ou bien le nombre de parenthèsages de longueur $n$). Dans ce cas la résolution de la relation de récurrence se transforme en la résolution d'une équation du second degré. Un autre exemple est le nombre $t_n$ de triplets d'entiers naturels de somme égale à $n$ (pour celui-ci nous avons déjà fait tous les calculs dans la Section 2.2, il suffit de considérer le développement de $\displaystyle{z \mapsto \frac{1}{(1-z)^3}}$ de deux manières distinctes), et encore bien d'autres.

En ce qui concerne les urnes aléatoires en général, il est possible de s'intéresser de plus près au système différentiel que nous leur avons associé, comme dans l'article [Flagolet, Dumas et Puyhaubert 2006]. Ainsi il devient possible d'étudier le comportement à long terme de certaines classes d'urnes aléatoires. Dans ce cas, il apparait que les proportions de boules rouges et bleues peuvent se comporter de manière bien plus étrange que dans le cas de l'urne de Pólya.

Bibliographie

Philippe Flajolet, Philippe Dumas, and Vincent Puyhaubert (2006). "Some exactly solvable models of urn process theory", Proceedings of Fourth Colloquium on Mathematics and Computer Science, vol. AG, p. 59–118.

Norman L. Johnson and Samuel Kotz (1977). Urns models and their application, John Wiley & Sons, New York-London-Sydney.

Pierre-Simon Laplace (1819). Théorie analytique des probabilités, Oeuvres complètes, Tome 7, Réédition 1886

Georges Pólya (1930). "Sur quelques points de la théorie des probabilités", Annales de l'institut Henri Poincaré, tome1, n° 2, p. 117-161

P. Tautu (1986). Stochastic spatial processes in biology : A concise historical survey, Lecture Notes in Math., vol. 1212, Springer-Verlag, Berlin and New York.

[1] Par exemple l'urne de Friedman. Celle-ci suit la règle suivante : lorsqu'on tire une boule d'une couleur, on ajoute une boule de l'autre couleur. Cette urne modélise par exemple une campagne électorale une élection pour laquelle les deux candidats sont tellement mauvais que toute personne écoutant l'un parler choisit aussitôt de voter pour l'autre (toute ressemblance avec une élection existante ou ayant existé est purement fortuite).

Urnes aléatoires, populations en équilibre et séries génératrices