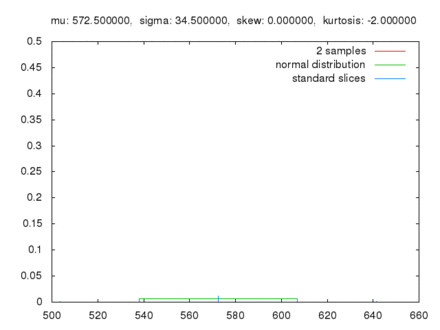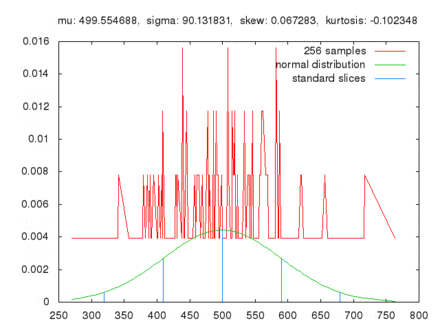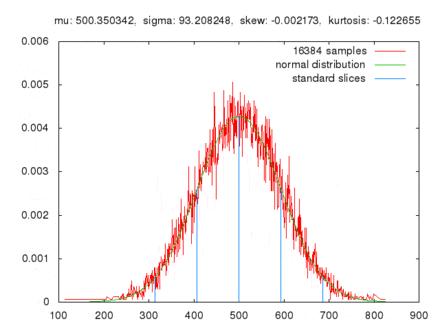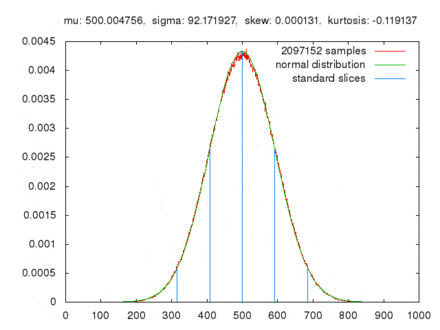
Comparaison de l'évolution de la somme de 10 tirages consécutifs entre 0 et 100 réalisés N fois. La distribution se rapproche d'une distribution normale quand N augmente.
Lien vers les vidéos sur Youtube
On rappelle ici l'énoncé du théorème et sa preuve:
Soit $ X_1, X_2,\dots$ une suite de variables aléatoires réelles définies sur le même espace de probabilité, indépendantes et identiquement distribuées suivant la même loi $D$.
Supposons que l'espérance $\mu$ et l'écart-type $\sigma$ de $D$ existent et soient finis avec $\sigma\not = 0$.
Considérons la somme
$$ S_n = X_1 + X_2 +\cdots + X_n.$$
Alors
- l'espérance de $S_n$ est $n\mu$ et
- son écart-type vaut ${\displaystyle \sigma {\sqrt {n}}} \sigma {\sqrt {n}}$.
De plus, quand $n$ est assez grand, la loi normale ${\displaystyle {\mathcal {N}}(n\mu ,n\sigma ^{2})}$ est une bonne approximation de la loi de $S_n$.
Afin de formuler mathématiquement cette approximation, nous allons poser
$${\displaystyle {\overline {X}}_{n}={\frac {S_{n}}{n}}={\frac {(X_{1}+X_{2}+...+X_{n})}{n}}}$$
et
$$ {\displaystyle \mathrm {Z} _{n}={\frac {\mathrm {S} _{n}-n\mu }{\sigma {\sqrt {n}}}}={\frac {{\overline {\mathrm {X} }}_{n}-\mu }{\sigma /{\sqrt {n}}}}}$$
de sorte que l'espérance et l'écart-type de $Z_n$ valent respectivement 0 et 1 : la variable est ainsi dite centrée et réduite.
Le théorème central limite énonce alors que la suite de variables aléatoires $Z_1, Z_2,\dots, Zn,\dots$ converge en loi vers une variable aléatoire $Z$, définie sur le même espace probabilisé, et de loi normale centrée réduite $ {\displaystyle {\mathcal {N}}(0,1)} $ lorsque $n$ tend vers l'infini.
Cela signifie que si $\phi$ est la fonction de répartition de $ {\displaystyle {\mathcal {N}}(0,1)} $, alors pour tout réel $z$ :
$${\displaystyle \lim _{n\to \infty }\mathrm {P} (\mathrm {Z} _{n}\leq z)=\Phi (z),}$$
ou, de façon équivalente :
$${\displaystyle \lim _{n\to \infty }\mathrm {P} \left({\frac {{\overline {\mathrm {X} }}_{n}-\mu }{\sigma /{\sqrt {n}}}}\leq z\right)=\Phi (z)}$$
Démonstration du théorème central limite :
Il existe de multiples preuves, en voici une très courte.
Pour une variable aléatoire $Y$ d'espérance $0$ et de variance $1$, la fonction caractéristique de $Y$ admet le développement limité :
$$ {\displaystyle \varphi _{\mathrm {Y} }(t)=1-{t^{2} \over 2}+\mathrm {o} (t^{2}),\quad t\rightarrow 0.}$$
Si $Y_i$ vaut $ {\displaystyle {\frac {\mathrm {X} _{i}-\mu }{\sigma }}} $, il est facile de voir que la moyenne centrée réduite des observations $X_1, X_2, \dots , X_n$ est simplement :
$$ {\displaystyle \mathrm {Z} _{n}={\frac {{\overline {\mathrm {X} }}_{n}-\mu }{\sigma /{\sqrt {n}}}}=\sum _{i=1}^{n}{\frac {\mathrm {Y} _{i}}{\sqrt {n}}}.}$$
D'après les propriétés élémentaires des fonctions caractéristiques, la fonction caractéristique de $Z_n$ est
$$ {\displaystyle \left[\varphi _{\mathrm {Y} }\left({\frac {t}{\sqrt {n}}}\right)\right]^{n}=\left[1-{\frac {t^{2}}{2n}}+\mathrm {o} \left({\frac {t^{2}}{n}}\right)\right]^{n}\longrightarrow \mathrm {e} ^{-t^{2}/2}} $$ lorsque ${\displaystyle n\rightarrow \infty }$.
Mais cette limite est la fonction caractéristique de la loi normale centrée réduite $ {\displaystyle {\mathcal {N}}(0,1)}$, d'où l'on déduit le théorème central limite grâce au théorème de convergence de Lévy, qui affirme que la convergence simple des fonctions caractéristiques implique la convergence en loi.