Vous pouvez retrouver cette question au format pdf.

Question du jeudi #62 : Quel est le rapport entre le volume d'un octaèdre régulier et celui d'un tétraèdre régulier de même côté ?

Nous allons proposer deux méthodes pour faire ce calcul, l'une calculatoire et l'autre géométrique.

1. Prenons le côté de nos polyèdres réguliers comme unité de longueur et calculons les deux volumes.
   Rappelons tout d'abord que le volume d'une pyramide $\Pi$ de hauteur $h$ et dont la base a une aire $A$ est
   \[ \textrm{vol}[\Pi] = \frac 13 \, A \, h.\]
   
   Une méthode pour se convaincre de ce fait est de découper la pyramide $\Pi$ en tranches. Si on note, pour $0 \leq t \leq h$, $P_t$ le plan parallèle à la base de la pyramide qui se trouve entre la base et le sommet, et à distance $t$ de celui-ci, la figure $\Pi \cap P_t$ est une image de la base $\Pi \cap P_h$, dilatée par un facteur $\frac th$, en vertu du théorème de Thalès. En particulier, on a $\textrm{aire}\left[\Pi \cap P_t\right] = \left(\frac th\right)^2 \, \textrm{aire}\left[\Pi \cap P_h\right] = \frac{t^2}{h^2}\, A$. On a alors
   \begin{align*}
   \textrm{vol}[\Pi] &= \int_0^h \textrm{aire}\left[\Pi \cap P_t\right]\, dt \\
   &= \int_0^h \frac{t^2}{h^2}\,A\,dt\\
   &= \frac{A}{h^2}\int_0^h t^2\,dt\\
   &= \frac 13 \, A\, h.
   \end{align*}
   
   On peut maintenant calculer le volume de nos deux polyèdres réguliers.
   • Le tétraèdre régulier est une pyramide dont la base est un triangle équilatéral de côté 1.
     
     
     
     En vertu du théorème de Pythagore, la hauteur de celui-ci est alors $\sqrt 3/2$ et son aire est donc
     \[ \textrm{aire}\left[\textrm{base}_{\textrm{tétraèdre}}\right] = \frac {\sqrt 3}4.\]
     
     Il reste à déterminer la hauteur $h_{\textrm{tétraèdre}}$ du tétraèdre régulier. En projetant le sommet sur la base, on obtient un triangle rectangle (en rouge sur la figure).
     
     
     
     Le pied de la hauteur ainsi construite est le centre de gravité de la base. Ainsi, le côté horizontal du triangle a une longueur $\frac 23 \times \frac {\sqrt 3}2 = \frac{\sqrt 3}3$. Comme l'hypothénuse du triangle rectangle mesure $1$, le théorème de Pythagore implique
     \[ h_{\textrm{tétraèdre}}^2 + \left(\frac {\sqrt 3}3\right)^2 = 1, \qquad \text{c'est-à-dire} \qquad h_{\textrm{tétraèdre}} = \sqrt{\frac 23} = \frac{\sqrt 6}3.   \]
     
     On a donc
     \begin{align*}
     \textrm{vol}[\textrm{tétraèdre}] &= \frac 13 \, \textrm{aire}\left[\textrm{base}_{\textrm{tétraèdre}}\right] \, h_{\textrm{tétraèdre}}\\
     & = \frac 13 \times \frac{\sqrt 3}4 \times \frac{\sqrt 6}3\\
     &= \frac{\sqrt 2}{12}.
     \end{align*}
   • De son côté, l'octaèdre régulier est obtenu en empilant l'une sur l'autre deux pyramides dont la base est un carré de côté $1$.
     
     
     
      Pour chacune d'elles, on a donc évidemment
     \[ \textrm{aire}\left[\textrm{base}_{\textrm{pyramide}}\right] = 1\]
     et il reste à déterminer leur hauteur $h_{\textrm{pyramide}}$.
     
     En projetant le sommet de l'une des pyramides sur la base, on obtient un triangle rectangle (en rouge sur la figure).
     
     
     
     L'hypothénuse de ce triangle mesure $1$, et les deux côtés de l'angle droit mesurent $\sqrt 2/2$ (c'est la moitié d'une diagonale du carré) et $h_{\textrm{pyramide}}$. Le théorème de Pythagore entraîne alors
     \[ \left(\frac{\sqrt 2}2\right)^2 + h_{\textrm{pyramide}}^2 = 1, \qquad \textrm{c'est-à-dire} \qquad h_{\textrm{pyramide}} = \frac{\sqrt 2}2.\]
     
     On a donc
     \begin{align*}
     \textrm{vol}[\textrm{octaèdre}] &= 2 \, \textrm{vol}[\textrm{pyramide}]\\
     &= \frac 23 \, \textrm{aire}\left[\textrm{base}_{\textrm{pyramide}}\right] \, h_{\textrm{pyramide}}\\
     & = \frac{\sqrt 2}3.
     \end{align*}

   En particulier,
   \[ \frac{\textrm{vol}\left[\textrm{octaèdre}\right]}{\textrm{vol}\left[\textrm{tétraèdre}\right]} = 4.\]

2. On peut également démontrer le même résultat par un découpage. Rappelons qu'en deux dimensions, si on enlève à un triangle équilatéral ses trois « pointes », c'est-à-dire les triangles équilatéraux deux fois plus petits inscrits dans le triangle initial et partageant un de ses sommets, la figure restante est elle-même un triangle équilatéral, isométrique aux pointes.
   
   
   
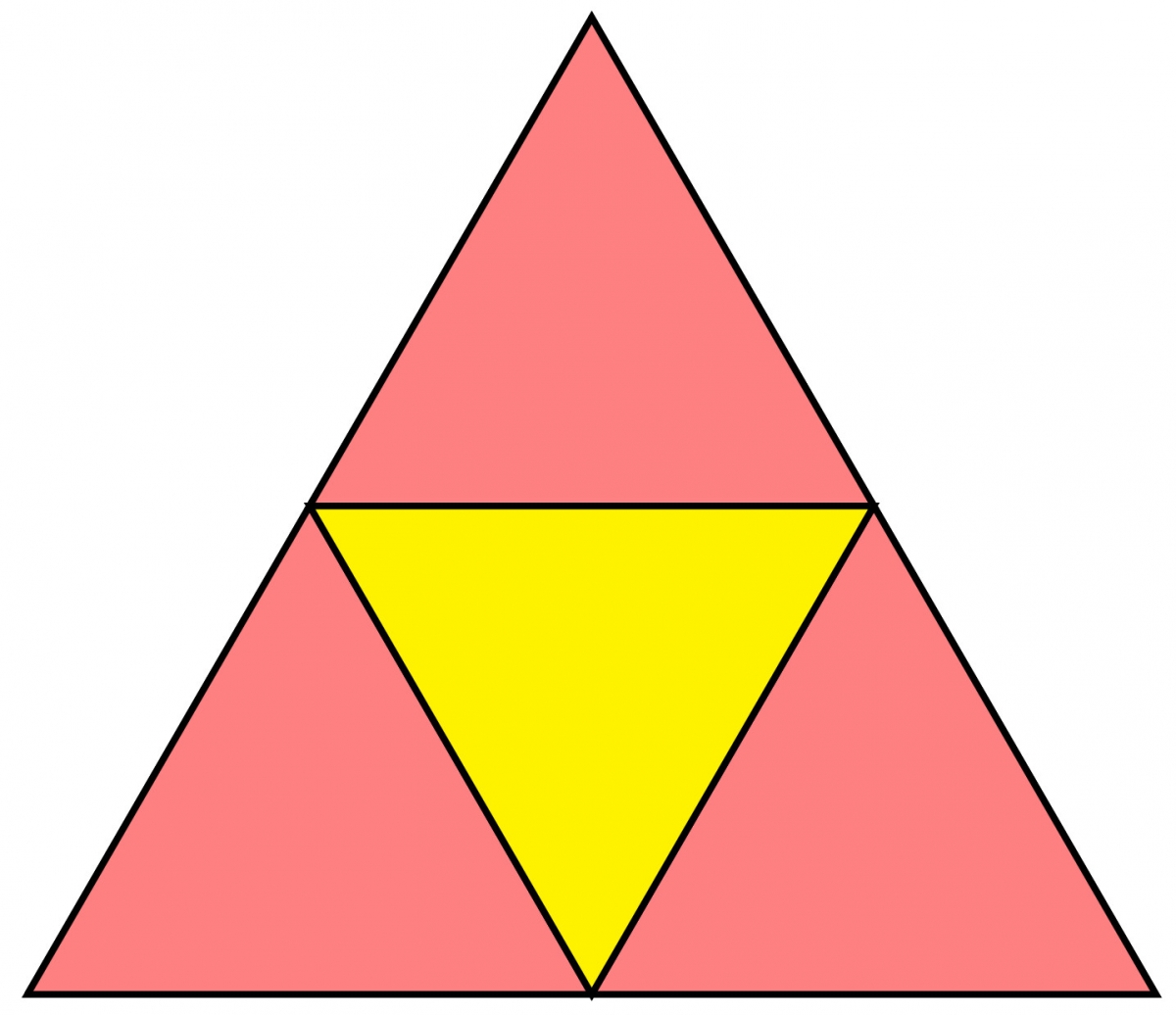
   Que se passe-t-il si l'on fait la même chose en trois dimensions, c'est-à-dire si l'on enlève les quatre pointes (qui sont quatre tétraèdres deux fois plus petits) à un tétraèdre régulier ? Comme le montrent les photos suivantes, on obtient un octaèdre régulier !
   
   
   
   En effet, la figure restante a deux types de faces (en bleu et jaune sur les images) : les faces (jaunes) qui sont incluses dans celles du tétraèdre initial et celles (bleues) qui proviennent de la découpe.
   
   Les premières sont exactement les triangles centraux du dessin en deux dimensions que l'on vient d'évoquer : ce sont bien des triangles équilatéraux. Les secondes sont des faces de tétraèdres réguliers, donc sont également des triangles équilatéraux. Comme une face jaune partage ses côtés avec des faces bleues, ces deux types de triangles font bien la même taille : on se retrouve donc bien avec un polyèdre régulier dont les huit faces sont des triangles équilatéraux, c'est-à-dire un octaèdre régulier.
   
   Il suffit alors de compter : les petits tétraèdres équilatéraux étant deux fois plus petits que l'initial, leur volume est 8 fois moindre. L'octaèdre central a donc un volume
   \begin{align*}
    \textrm{vol}[\textrm{octaèdre}]&=\textrm{vol}[\textrm{grand tétraèdre}] - 4\,\textrm{vol}[\textrm{petit tétraèdre}]\\
   &=8\,\textrm{vol}[\textrm{petit tétraèdre}] - 4\,\textrm{vol}[\textrm{petit tétraèdre}]\\
   &=4\,\textrm{vol}[\textrm{petit tétraèdre}].
   \end{align*}
   
   Les petits tétraèdres et l'octaèdre central ayant les mêmes côtés, on a donc encore une fois montré que le rapport des volumes était de $4$.
   
   Voici également une animation illustrant le découpage du tétraèdre en quatre petits tétraèdres et un octaèdre.
   
   

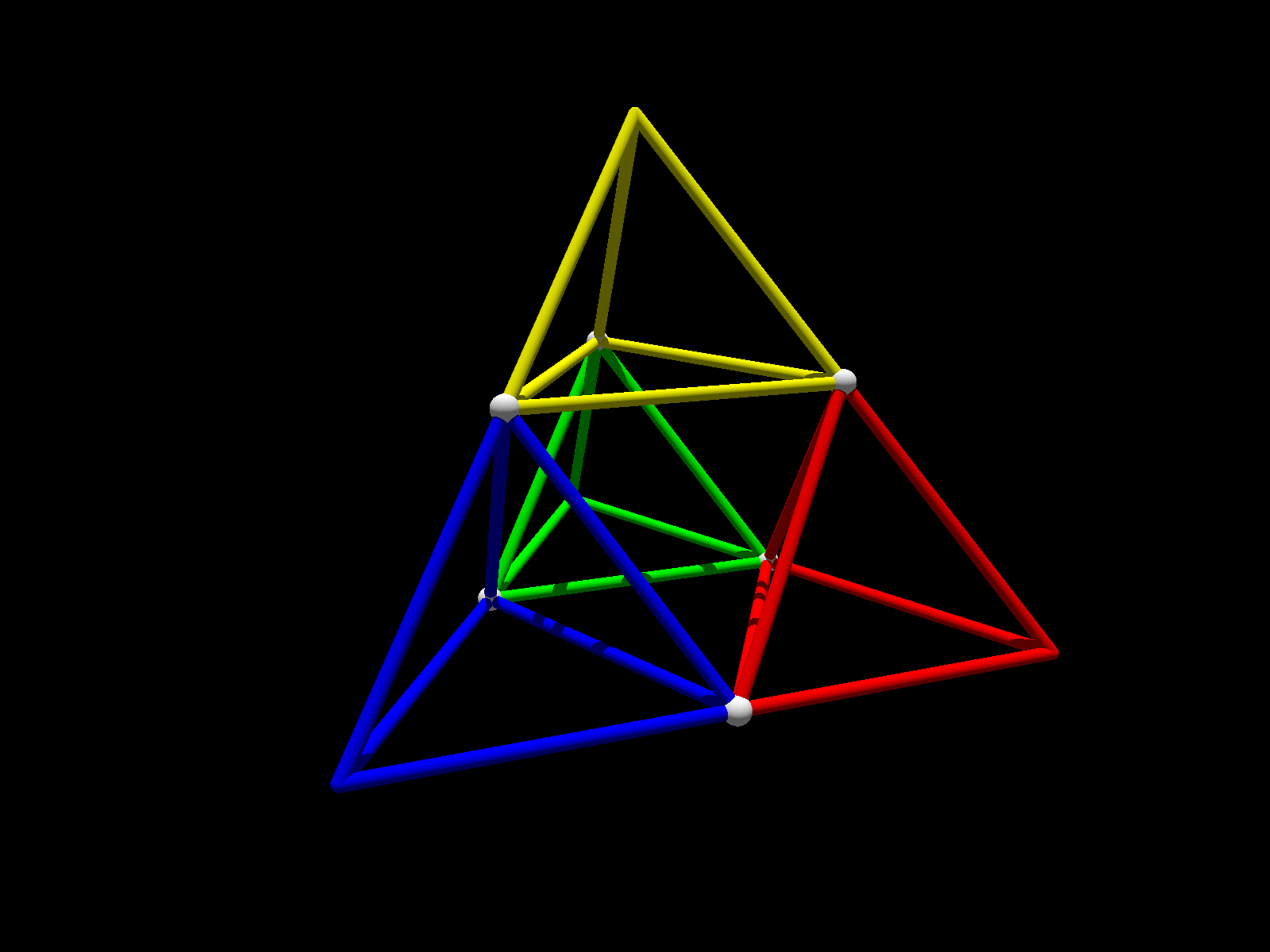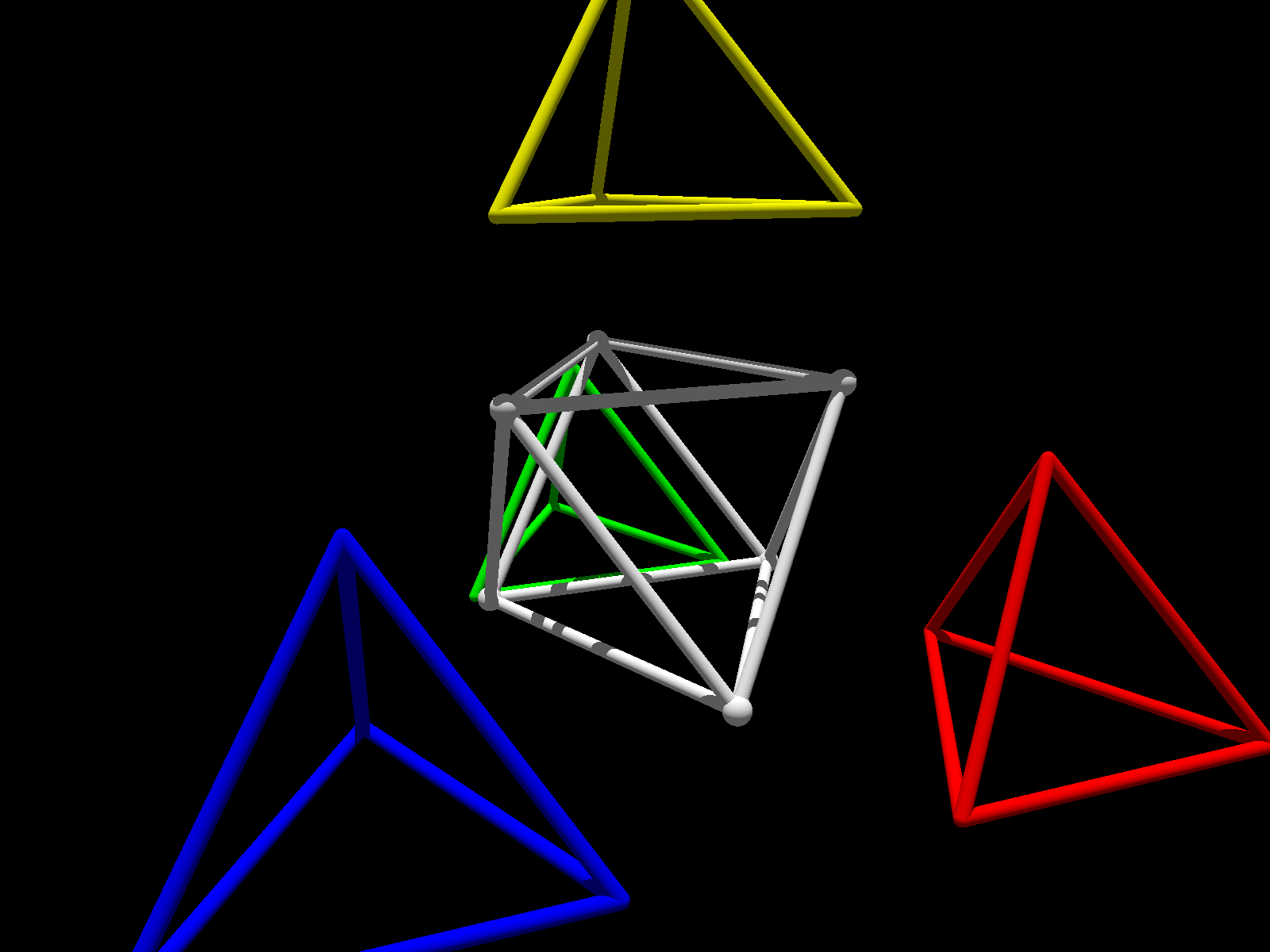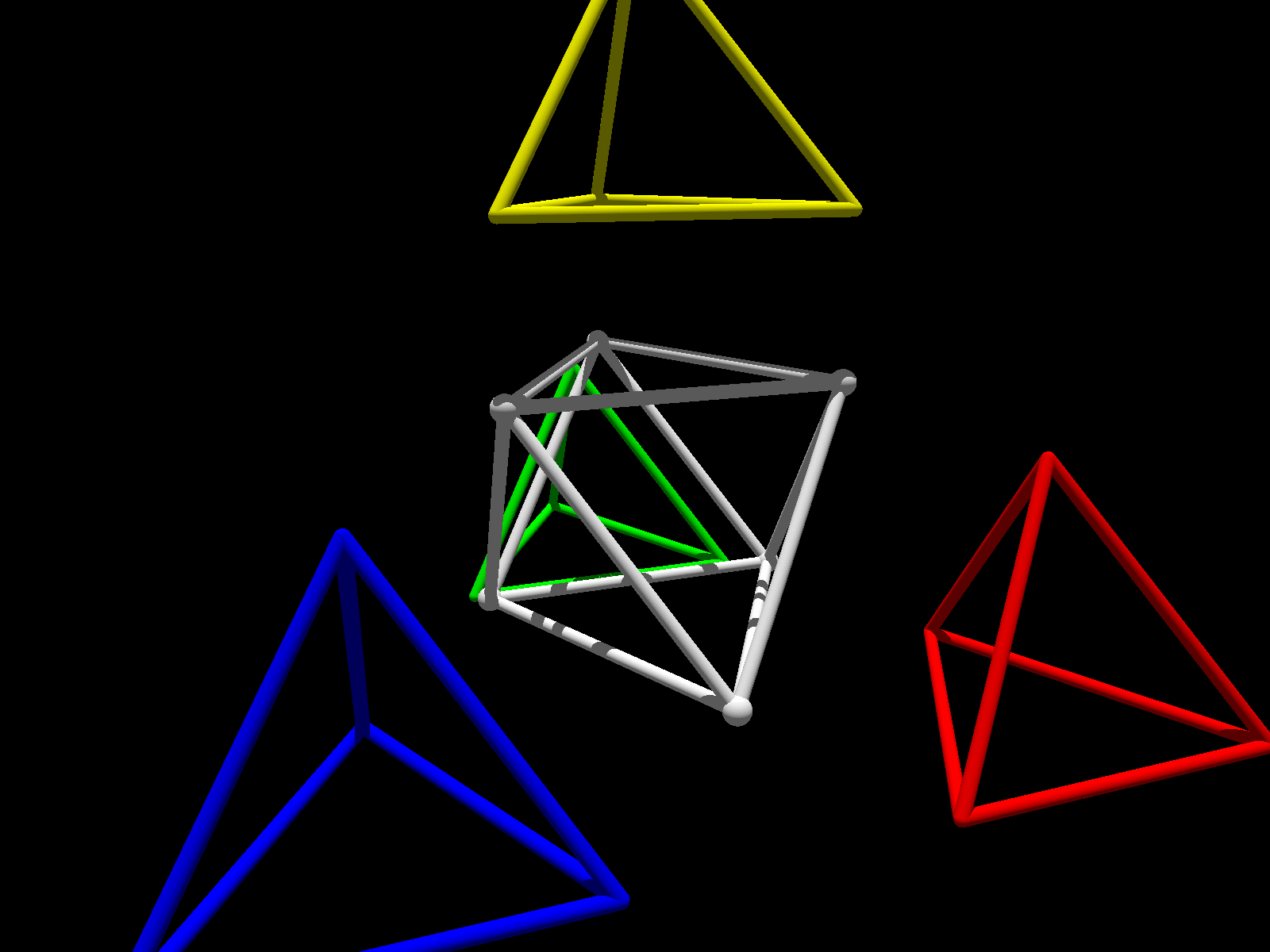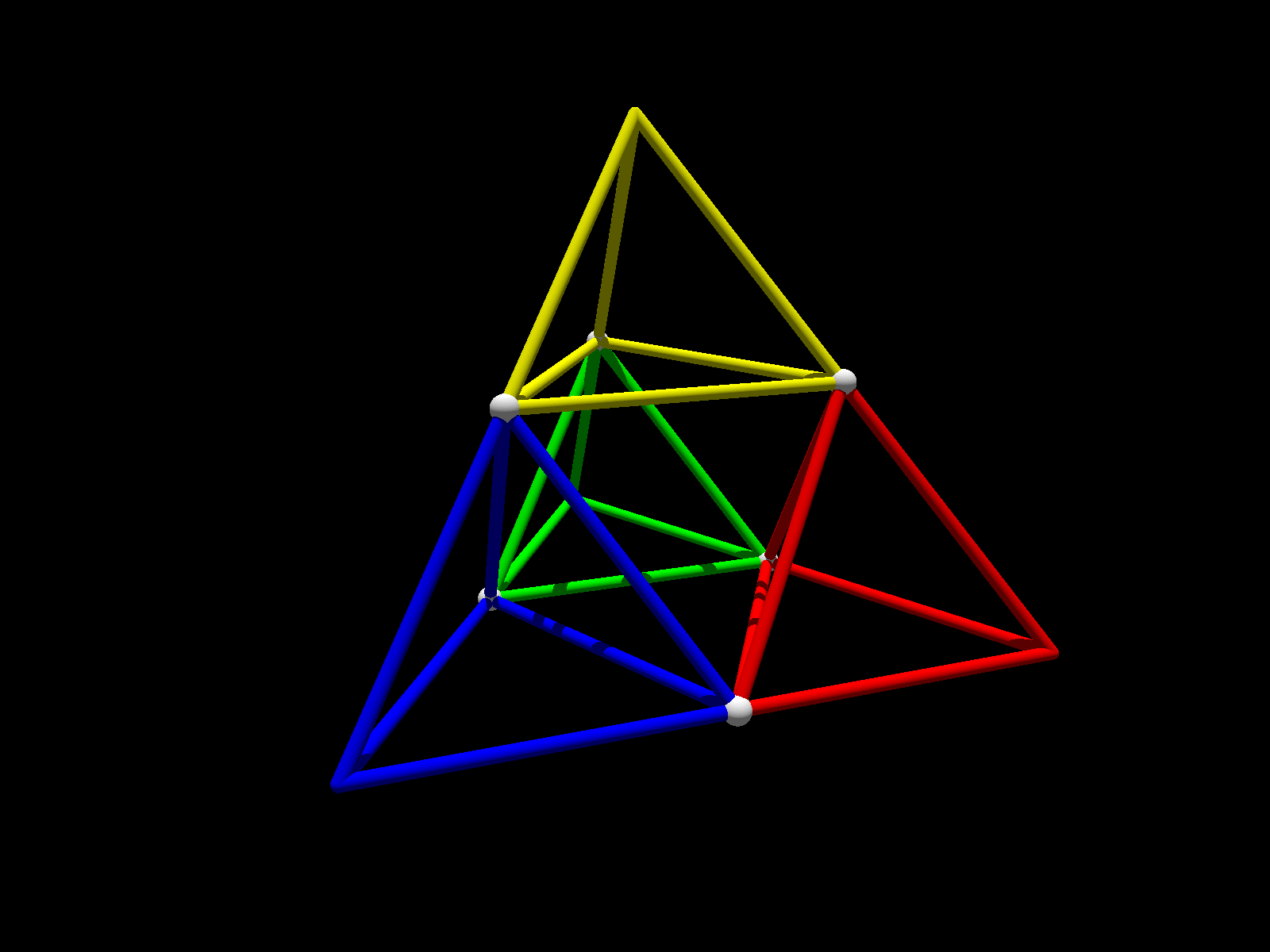
Crédit photos : Clément Caubel.

Les images (et l'animation) en 3D ont été réalisées avec POV-Ray.