Vous pouvez retrouver cette question au format pdf.

Question du jeudi #56 : À l'occasion de la journée Sophie Germain ayant lieu demain à l'Institut Henri Poincaré (avec notamment le lancement du timbre à son effigie), la question du jour est un résultat qui lui est attribué.

Montrer que pour tout $n > 1$, le nombre $n^4 + 4$ n'est pas premier.
 

La réponse tient en une ligne :
\[ n^4 + 4 = (n^2 - 2n + 2)(n^2 + 2n +2).\]

(Évidemment, il faut aussi dire que si $n \geq 2$, alors $n^2 \geq 2n$ donc les deux facteurs sont au moins égaux à $2$, et la factorisation n'est pas triviale.)

Même si la factorisation ci-dessus se démontre directement en développant, il peut être intéressant d'expliquer comment on peut l'obtenir sans la connaître a priori. Donnons deux arguments différents.

1. Une méthode efficace quoique détournée pour factoriser un entier ou une expression algébrique repose sur l'identité remarquable $x^2 - y^2 = (x-y)(x+y)$ (c'est peut-être la meilleure façon de se souvenir que $91 = 100 - 9$ n'est pas premier, par exemple !) Cette méthode s'applique ici assez directement :
   \[\begin{align*}
   n^4 +4 &= n^4 + 4n^2 + 4 - 4n^2\\
   &= (n^2 + 2)^2 - (2n)^2\\
   &= (n^2 - 2n + 2)(n^2 + 2n +2).
   \end{align*}\]
2. Si l'on veut retrouver la formule sans faire appel à aucune astuce de quelle sorte que ce soit, l'approche la plus systématique est de factoriser le polynôme $X^4 + 4$ d'abord dans $\mathbb C$ puis dans $\mathbb R$. Si on note $\zeta = \zeta_8 = \exp\left(\frac{2i \pi}8\right) = \frac{\sqrt 2}2 + \frac{\sqrt 2}2i$ (de telle sorte que les racines huitièmes de l'unité soient exactement les puissances de $\zeta$, et donc que les racines quatrièmes de $-1$ soient exactement $\zeta$, $\zeta^3$, $\zeta^5$, $\zeta^7$), les racines du polynôme sont les nombres $\zeta \sqrt 2$, $\zeta^3 \sqrt 2$, $\zeta^5 \sqrt 2$ et $\zeta^7 \sqrt 2$, ce qui donne la factorisation
   \[ X^4 + 4 = \left(X - \zeta \sqrt 2\right) \left(X - \zeta^3 \sqrt 2\right)\left(X - \zeta^5 \sqrt 2\right)\left(X - \zeta^7 \sqrt 2\right).\]
   
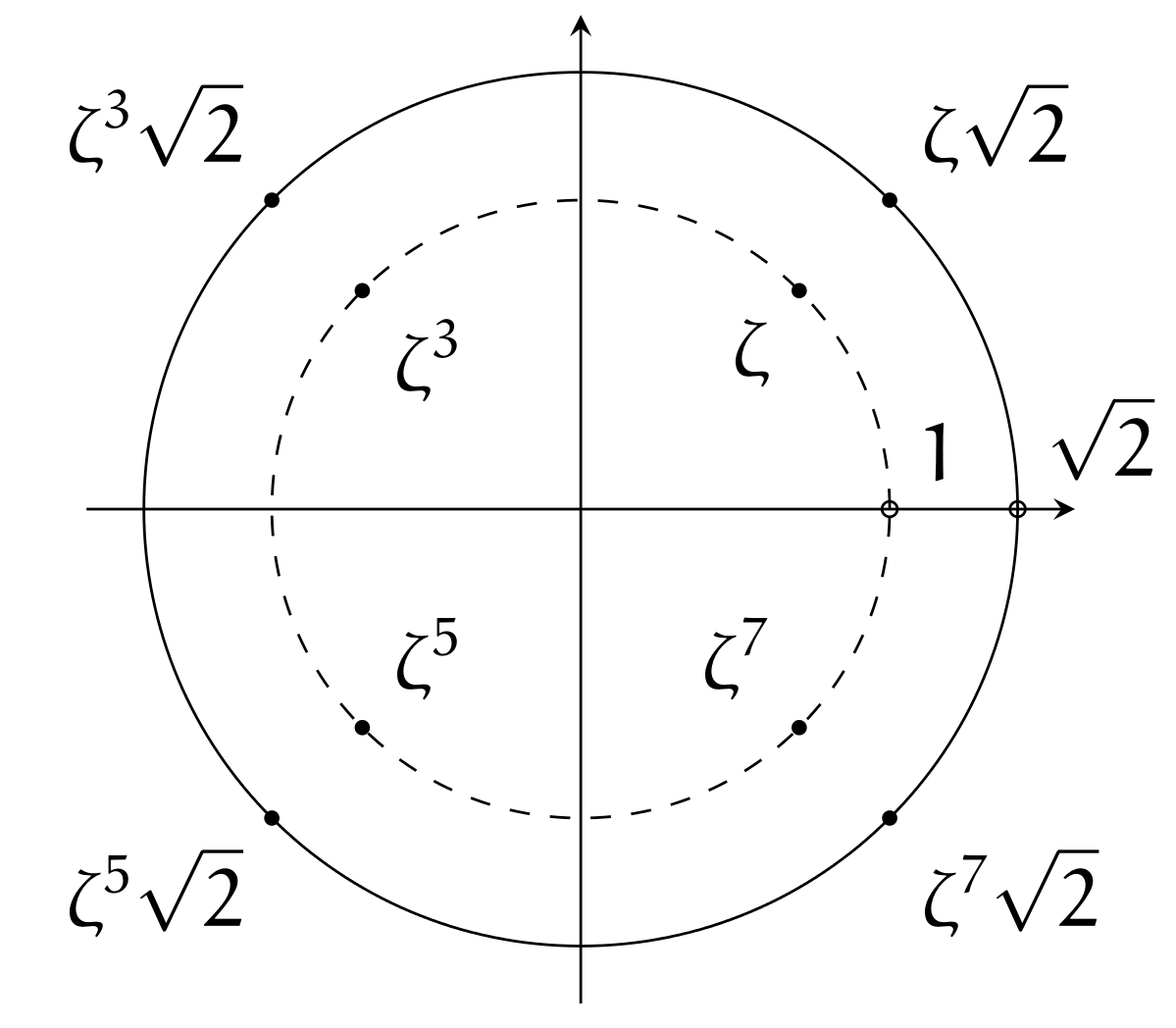
   Pour obtenir la factorisation dans $\mathbb R$, il faut maintenant regrouper les racines conjuguées ; on obtient alors les facteurs
   \[\begin{align*}
   \left(X - \zeta \sqrt 2\right)\left(X - \zeta^7 \sqrt 2\right) &= X^2 - 2X + 2\\
    \left(X - \zeta^3 \sqrt 2\right)\left(X - \zeta^5 \sqrt 2\right) &= X^2 +2X + 2,
   \end{align*}\]
   ce qui démontre bien l'identité recherchée :
   \[X^4 + 4 = (X^2 - 2X + 2)(X^2 + 2X+2).\]

Remarque. Sous la forme
\[ a^4 + 4b^4 = (a^2 - 2ab + 2b^2) (a^2 + 2ab + 2b^2),\]
cette identité est connue sous le nom d'identité de Sophie Germain, cf. par exemple le livre Solutions d'expert d'Arthur Engel (éditions Cassini, 2007).

Sophie Germain (1776-1831) a effectivement démontré (par une autre méthode) que les nombres de la forme $n^4 + 1$ n'étaient jamais premiers, cf. par exemple le site Theorem of the day et les références qu'il contient.