Vous pouvez retrouver cette question au format pdf.

Question du jeudi #48 : Lors d'un tournoi de Quidditch, quatre équipes s'affrontent une fois chacune. Le tableau suivant indique le vainqueur de chaque match.

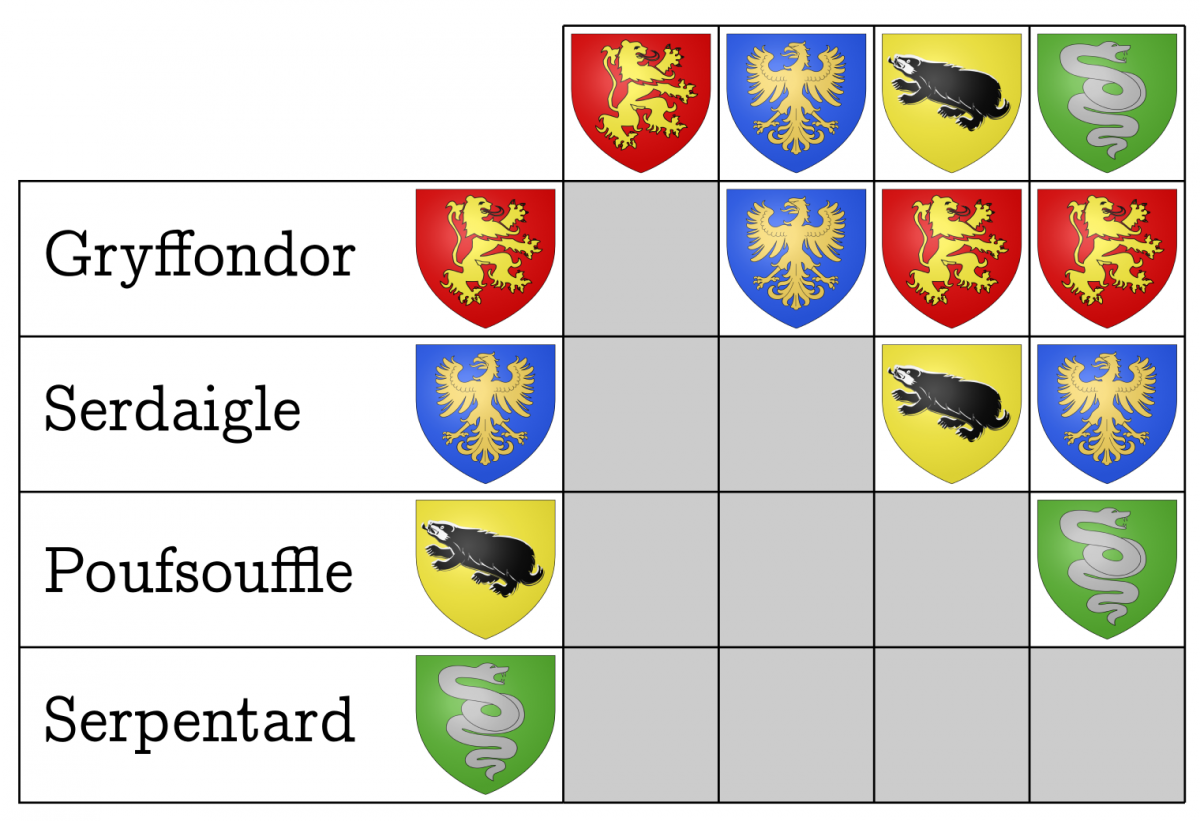
Il est alors possible de lister les équipes, de telle sorte que chacune ait battu la suivante : par exemple, Gryffondor a battu Poufsouffle, qui a battu Serdaigle, qui a battu Serpentard.

Est-il toujours possible de faire une telle liste ? Quid si le tournoi voit s'affronter plus de quatre équipes ?

On supposera dans cette question qu'un match de Quidditch ne peut pas être nul (ce qui est discutable).

La réponse est qu'une telle liste est toujours possible. Montrons-le par récurrence sur le nombre de joueurs. Si le tournoi voit s'affronter deux équipes (il n'y a donc qu'un match), c'est évident : on peut dire que le vainqueur a battu le perdant. (C'est également évident pour un tournoi à une équipe et pas de match, si l'on n'a pas peur des raisonnements sur l'ensemble vide).

Supposons donc que le résultat soit vrai pour tous les tournois à $n$ équipes, et essayons d'en déduire le résultat pour $n+1$ équipes : on peut commencer par oublier une équipe (que l'on notera $\textrm{É}_0$) et regarder simplement les matchs ayant opposé les $n$ autres. D'après l'hypothèse de récurrence, on peut numéroter les équipes restantes $\textrm{É}_1, \textrm{É}_2, \ldots, \textrm{É}_n$ de telle sorte que $\textrm{É}_1$ ait battu $\textrm{É}_2$, qui ait battu $\textrm{É}_3$, etc. jusqu'à $\textrm{É}_{n-1}$ qui a battu $\textrm{É}_n$.

Cherchons à insérer $\textrm{É}_0$ dans cette liste. Si elle a battu $\textrm{É}_1$, on peut simplement la rajouter au tout début. De même, si elle a perdu contre $\textrm{É}_n$, on peut la rajouter tout à la fin. On peut donc supposer dans la suite du raisonnement que ce n'est pas le cas.

On peut alors regarder le plus petit numéro $1 \leq i \leq n$ tel que $\textrm{É}_0$ ait gagné contre $\textrm{É}_i$. Comme elle a gagné contre $\textrm{É}_n$, il existe en effet de tels numéros. Comme elle a perdu contre $\textrm{É}_1$, on sait même que $i \geq 2$. Puisque $i$ est le plus petit tel numéro, on sait en particulier que $\textrm{É}_0$ a perdu contre $\textrm{É}_{i-1}$.

On peut alors simplement insérer $\textrm{É}_0$ entre les équipes $\textrm{É}_{i-1}$ et $\textrm{É}_i$ : $\textrm{É}_1$ a battu $\textrm{É}_2$, qui a battu $\textrm{É}_3$, ... qui a battu $\textrm{É}_{i-2}$, qui a battu $\textrm{É}_{i-1}$, qui a battu $\textrm{É}_0$, qui a battu $\textrm{É}_i$, qui a battu $\textrm{É}_{i+1}$, etc.

Cela prouve donc que tous les tournois possèdent cette propriété.

Remarque. On peut traduire ce résultat en termes de graphes. En théorie des graphes, un tournoi est une orientation du graphe complet $K_n$, c'est-à-dire un graphe orienté tel qu'il existe exactement une arête entre deux sommets quelconques. On interprête l'existence d'une arête allant de $v$ à $w$ comme voulant dire que $v$ a battu $w$. Par exemple, notre tournoi de Quidditch correspond au graphe suivant.

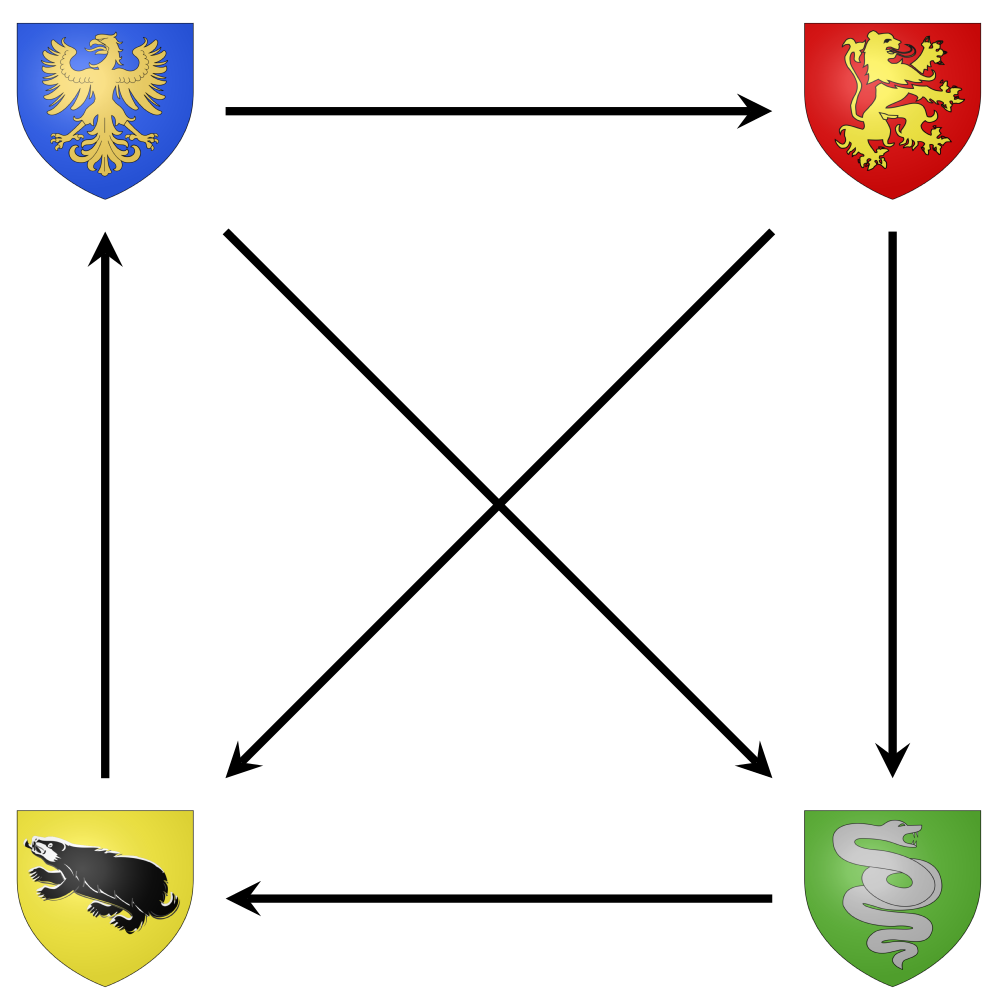
Le résultat que l'on vient de montrer se traduit alors en le fait que tout tournoi possède un chemin hamiltonien dirigé, c'est-à-dire un chemin respectant le sens des flèches et passant par tous les sommets. Celui de notre exemple est ici indiqué en rouge.

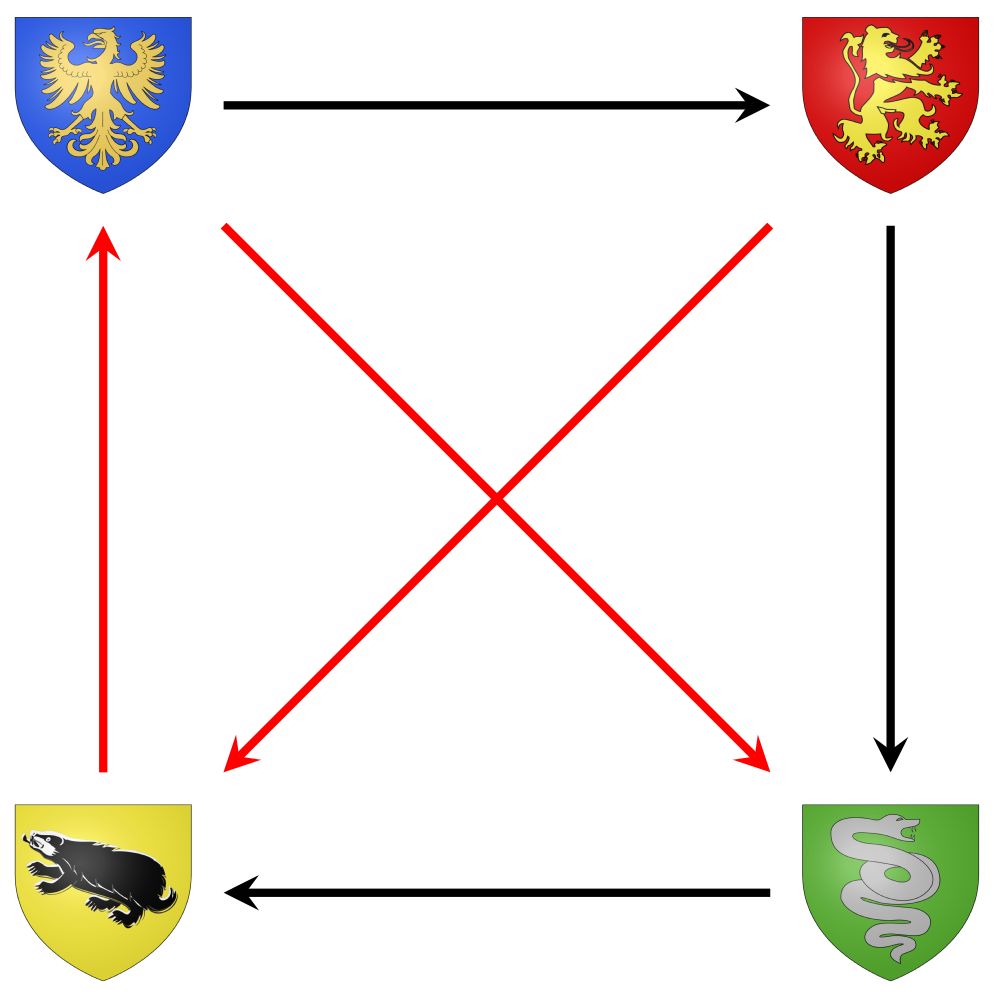
Ce résultat est dû au mathématicien hongrois László Rédei, et date de 1934.

La littérature sur les tournois est conséquente. On pourra consulter l'article Probabiliser sur le site Images des Mathématiques pour un autre résultat sur ces objets, dont la preuve fait appel à des notions de probabilités élémentaires.