Vous pouvez retrouver cette question au format pdf.

Question du jeudi #42 : On voit facilement qu'il est possible de recouvrir un carré par quatre triangles équilatéraux de même côté.

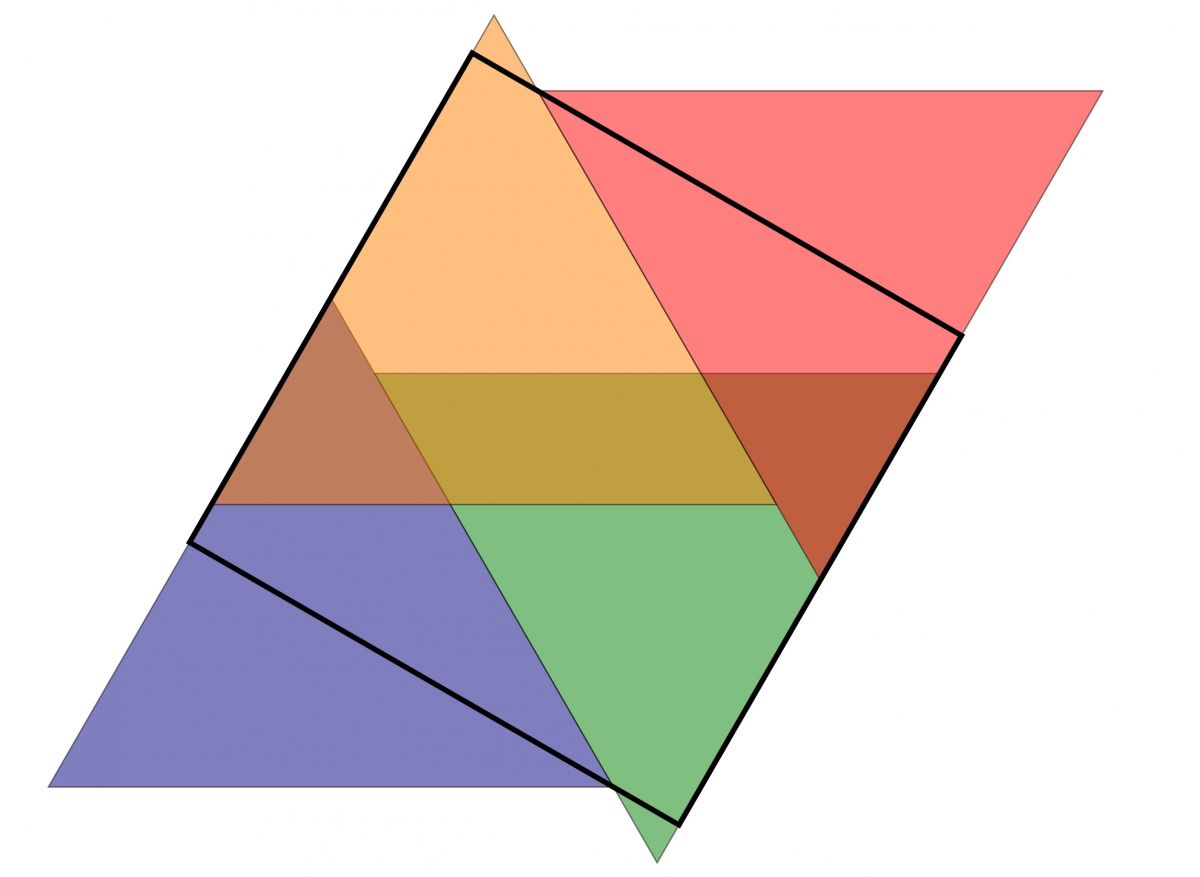
Est-il possible de n'en utiliser que trois ?

On se convainc très vite que la réponse est non. Démontrons-le. Choisissons la longueur des côtés de notre carré et nos triangles comme unité de longueur.

On peut arriver rapidement à une démonstration en considérant les sommets du carré. Puisqu'il y a quatre sommets et trois triangles, il est nécessaire qu'un des triangles recouvre deux des sommets du triangle. Cela entraîne qu'un de ses côtés coïncide avec l'un des côtés du carré. Appelons [AB] ce côté.

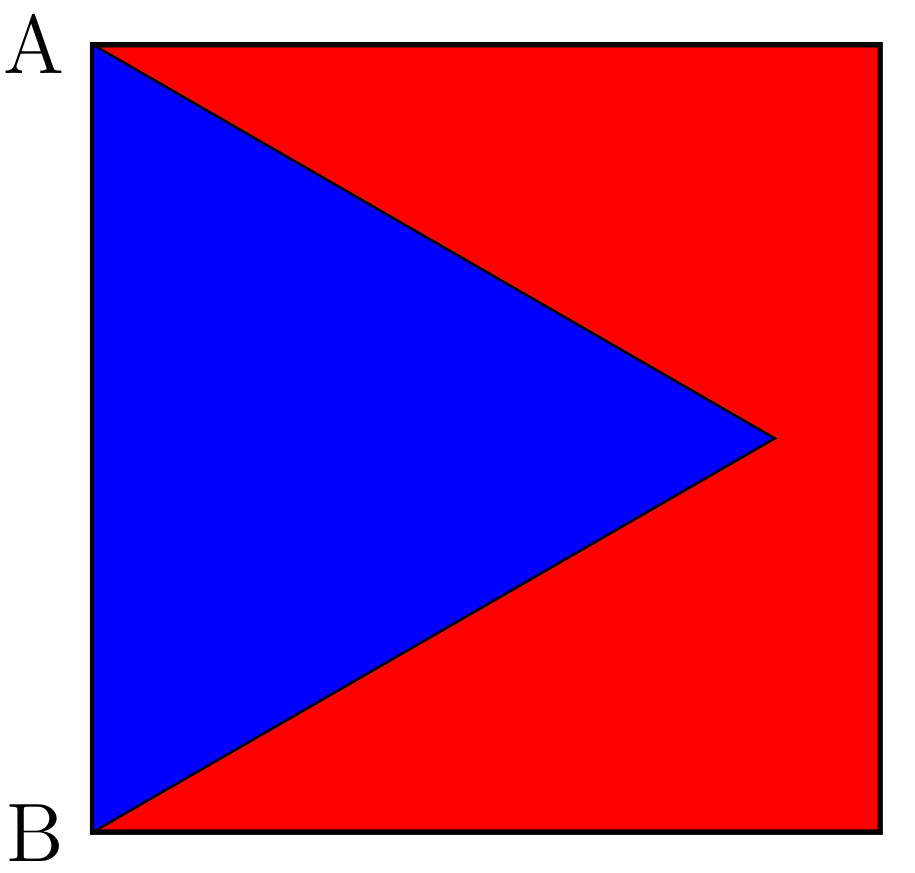
On peut alors trouver des points non couverts par le triangle aussi proches qu'on le souhaite de A. Cela entraîne qu'un des autres triangles doit également couvrir A. Puisque la situation est symétrique, on peut en dire autant de B. Ainsi, les trois triangles que l'on considère doivent tous les trois couvrir A ou B.

Cependant, la distance entre A (ou B) et le milieu du côté opposé à AB vaut $\sqrt 5/2 > 1$ en vertu du théorème de Pythagore. En particulier, aucun de nos triangles ne peut couvrir ce point, ce qui achève la preuve.