Vous pouvez retrouver cette question au format pdf.

Question du jeudi #39 : On place n points sur un cercle et l'on trace toutes les cordes reliant ces deux points. On suppose en outre que les cordes sont en position générale, c'est-à-dire que trois cordes ne sont jamais concourantes.

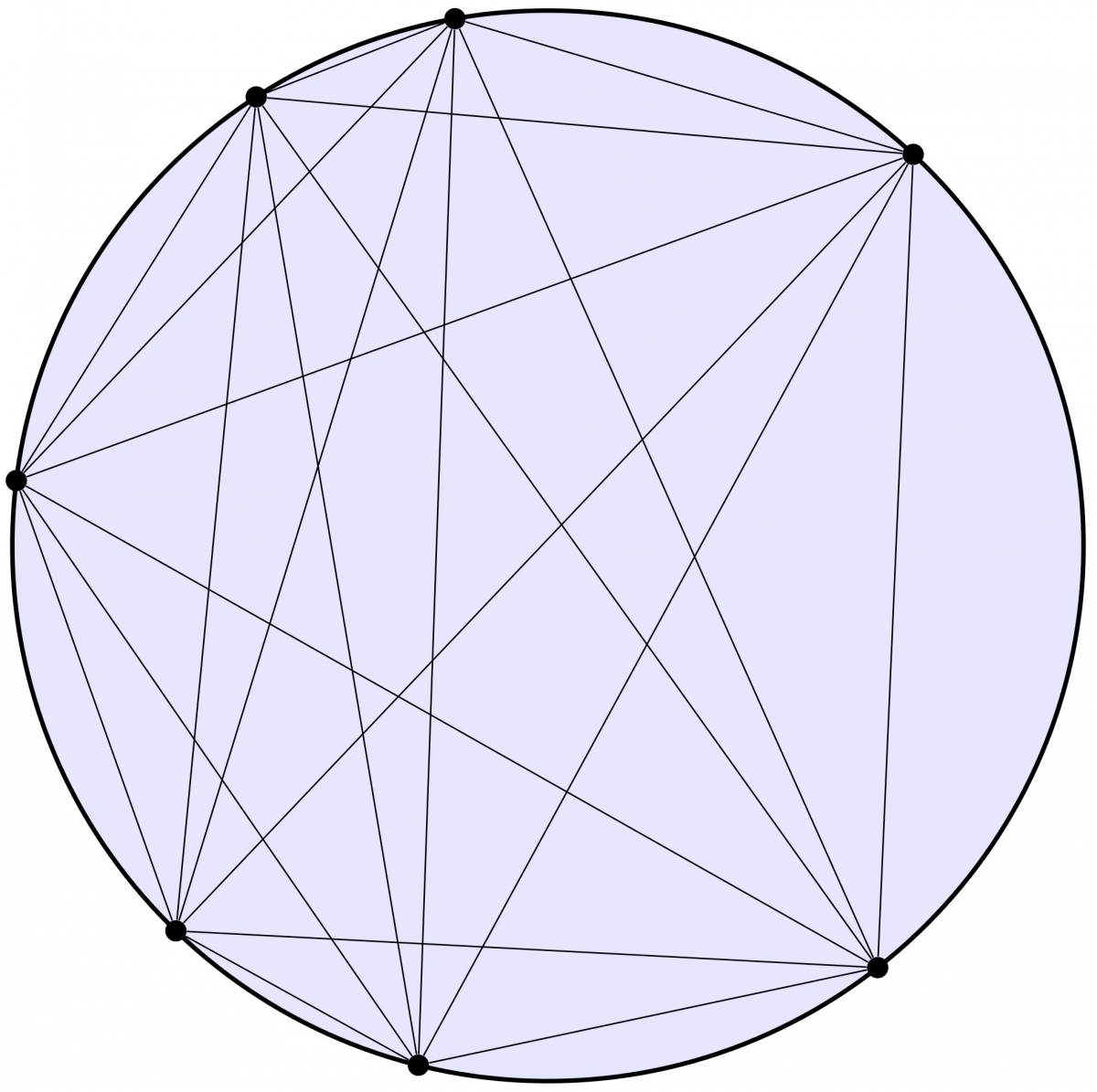
Combien de points d'intersection y aura-t-il à l'intérieur du disque ?

La réponse est étonnament simple, si on effectue le dénombrement habilement.

Chaque point d'intersection met en jeu quatre points sur le cercle : les extrémités des deux cordes qui s'intersectent (les deux cordes ne peuvent pas partager une extrémité puisque leur intersection se trouve à l'intérieur du disque). Puisque trois cordes ne sont jamais concourantes, ces quatre points sont bien définis, sans ambigüité.

Réciproquement, étant donné quatre points sur un cercle, les six cordes ainsi formées dessinent un quadrilatère convexe et ses deux diagonales. Parmi ces six cordes, seulement deux s'intersectent à l'intérieur du disque : les deux diagonales.

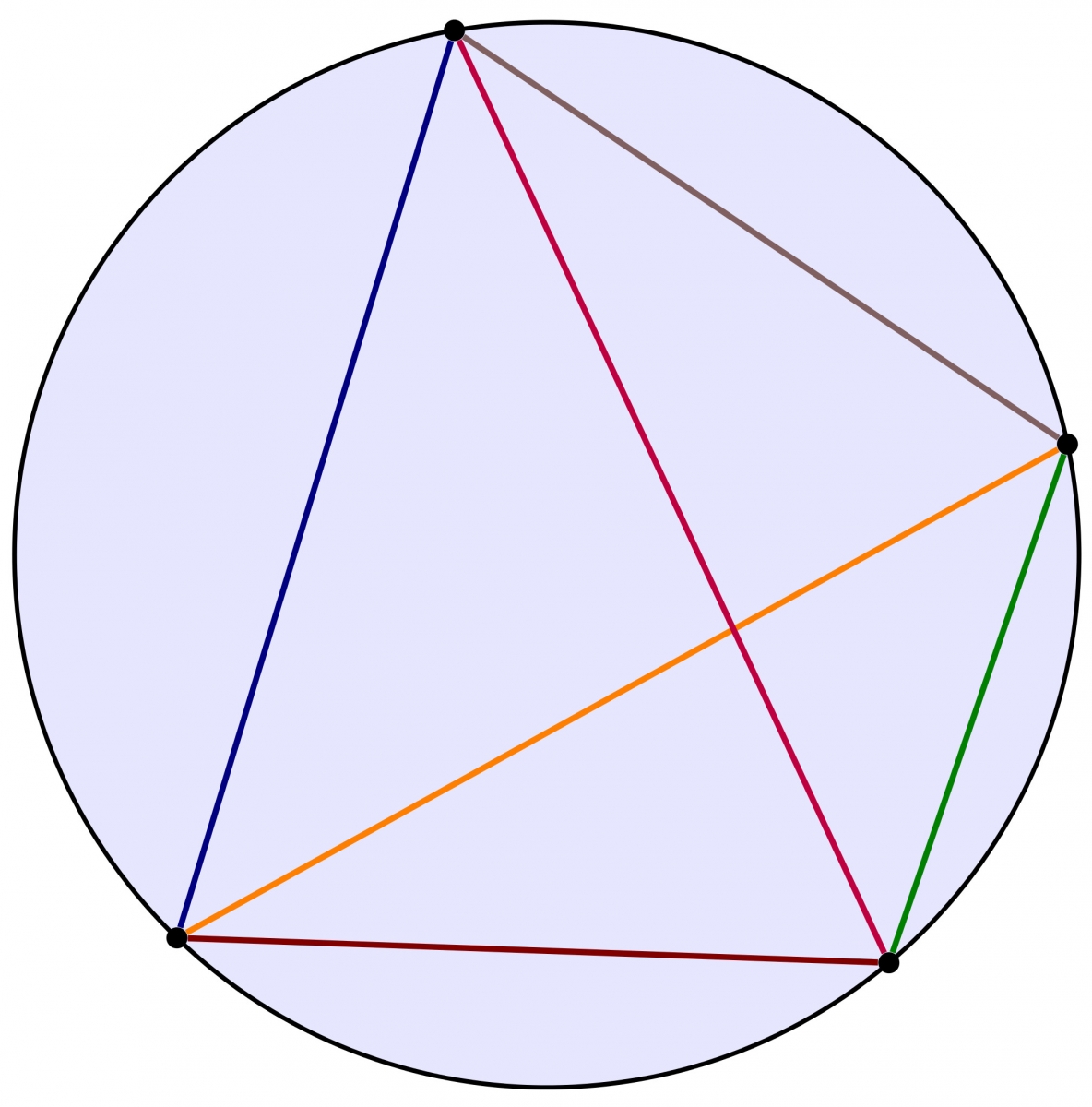
Ainsi, il y a exactement autant de points d'intersection à l'intérieur du disque que d'ensembles de quatre points choisis parmi les $n$ que nous avons placés, c'est-à-dire $\binom n 4$.