Vous pouvez retrouver cette question au format pdf.

Question du jeudi #36 : On se donne $n$ vecteurs $\vec v_1, \ldots, \vec v_n$ du plan dont la somme des longueurs vaut $1$. Montrer qu'il est possible de trouver une partie $S \subset \{1, 2, \ldots, n\}$ telle que la somme correspondante \[ \sum_{i \in S} \vec v_i\] ait une longueur au moins égale à $\frac 16$.

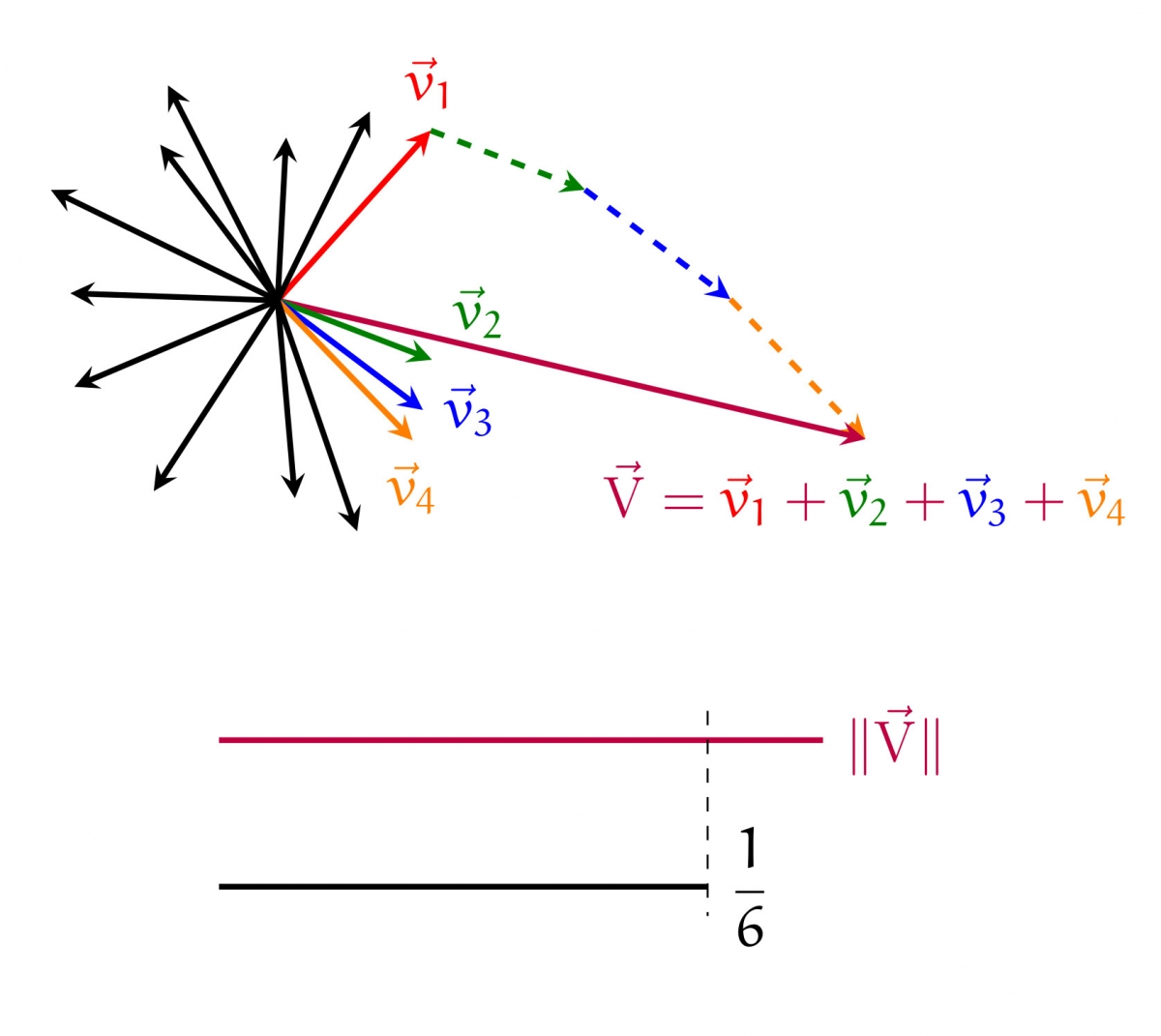
Le problème est évidemment de réussir à choisir des vecteurs dont la somme présente peu de compensations, et qui pointent donc dans des directions proches. Nous allons choisir des vecteurs appartenant à un même secteur angulaire d'angle $2 \theta$ (pour $\theta < \pi / 2$).

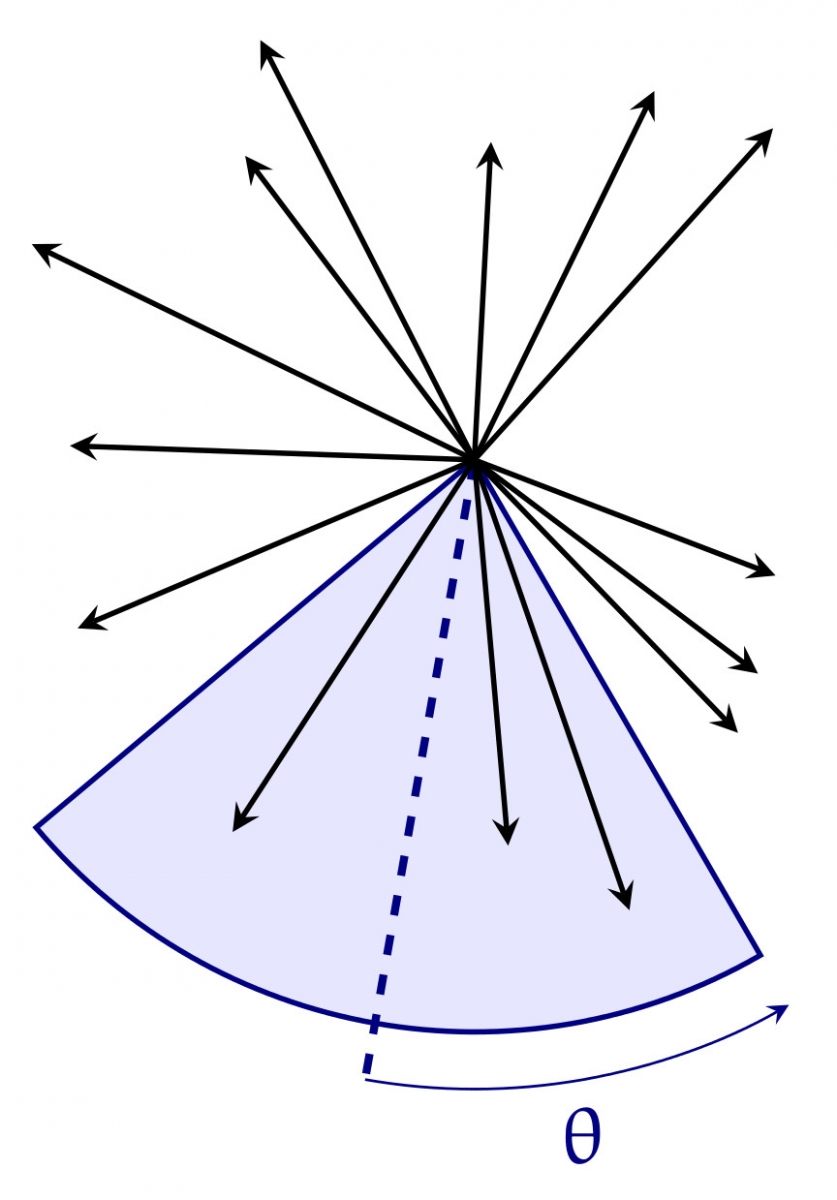
On peut alors facilement minorer la longueur de la somme $\vec V$ de ces vecteurs. En effet, si $\vec v$ est un vecteur de longueur $\ell$ dans un secteur d'angle $2 \theta$, son projeté $p(\vec v)$ sur la bissectrice du secteur a pour longueur $\ell\, \cos \alpha$, où $\alpha$ est l'angle indiqué sur la figure.

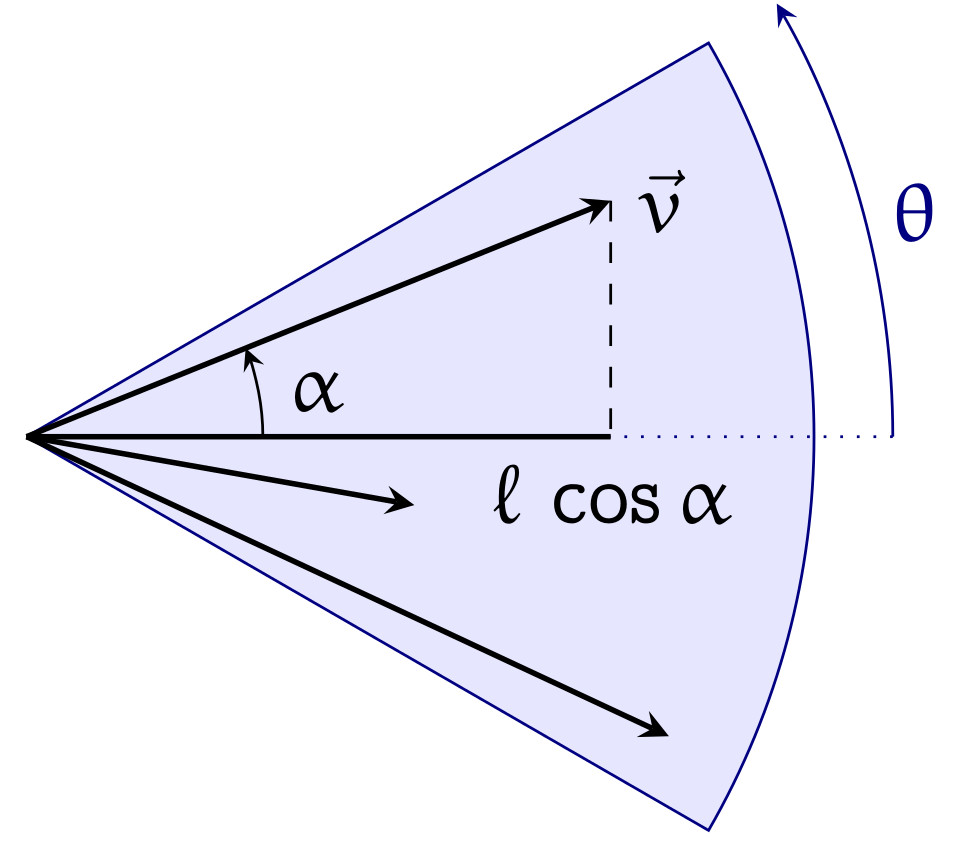
Comme $\alpha \leq \theta$ et que $\cos$ décroît sur $[0,\pi/2]$, le projeté $p(\vec v)$ a donc une longueur \[ \| p(\vec v) \| \geq \ell\, \cos(\theta).\]

Ainsi, si notre secteur contient $r$ vecteurs $\vec v_1, \ldots, \vec v_r$ de longueurs $\ell_1, \ldots, \ell_r$, tous les projetés $p(\vec v_i)$ pointent dans la même direction et on a \begin{align*} \|p(\vec v_1) + \cdots + p(\vec v_r)\| &= \| p(\vec v_1) \| + \cdots + \| p(\vec v_r) \|\\ &= \ell_1 \, \cos \alpha_ 1 + \cdots + \ell_r\,\cos \alpha_r\\ &\geq \ell_1\, \cos \theta + \cdots + \ell_r\,\cos \theta\\ &= \left(\ell_1 + \cdots + \ell_r\right)\,\cos \theta. \end{align*}

Or, la somme des projetés $p(\vec v_1) + \cdots + p(\vec v_r)$ n'est rien d'autre que le projeté du vecteur $\vec V = \vec v_1 + \cdots + \vec v_r$. Si elle est de longueur $\geq L\,\cos \theta$, c'est que le vecteur $\vec V$ lui-même vérifie : \[ \| \vec V \| \geq L\,\cos \theta,\] où $L$ est la somme des longueurs des vecteurs inclus dans notre secteur.

On a donc trouvé une manière de choisir des vecteurs de manière à pouvoir minorer leur longueur totale : on se trouve maintenant face à un problème d'optimisation. En effet, il va falloir choisir habilement notre secteur (et notamment son angle d'ouverture $\theta$) de manière à obtenir $L\,\cos \theta$ aussi grand que possible. Évidemment, plus le secteur est grand, plus il contiendra de vecteurs (et donc plus $L$ sera grand), mais plus le facteur « de perte » $\cos \theta$ sera petit.

Déjà, remarquons que la longueur totale de tous les vecteurs est de $1$. Ainsi, un secteur d'angle $2 \theta$ contiendra « en moyenne » des vecteurs dont la somme des longueurs vaut \[L_{\textrm{moy}} = \frac{2 \theta}{2 \pi} = \frac \theta \pi.\] En particulier, on peut trouver[fn]Si on veut être parfaitement rigoureux, on peut invoquer un argument de calcul intégral pour justifier cette affirmation. Ce n'est cependant pas strictement nécessaire, puisque, le nombre de vecteurs étant fini, il n'y a qu'un nombre fini de possiblités pour l'ensemble des vecteurs qu'un secteur d'angle $\theta$ peut contenir et donc pour la somme $L$ des longueurs correspondantes. La « moyenne » $\theta / \pi$ sur laquelle on raisonne est alors une moyenne pondérée de ces valeurs de $L$ et il faut bien qu'une de ces valeurs soit supérieure ou égale à $\theta / \pi$.
Quelle que soit la manière rigoureuse dont on le formule, l'argument (qui peut paraître anodin) crucial que l'on utilise est très intuitif : dans une famille de nombres, il en existe au moins un qui est supérieur ou égal à la moyenne. Il s'agit simplement de la contraposée de l'affirmation (encore plus évidente) : la moyenne d'une famille de nombres est comprise entre ses valeurs extrêmes. Pour insignifiant que cet argument puisse paraître, il est en fait d'une grande portée. C'est notamment lui qui se cache derrière le célèbre principe des tiroirs. On pourra consulter (en anglais) cet article du grand informaticien Edsger W. Dijkstra pour une comparaison fort instructive entre ces deux principes.[/fn] un secteur d'angle $2 \theta$ tel que la somme des longueurs des vecteurs qu'il contient soit \[ L \geq \frac \theta \pi.\]

Tout cela démontre que quel que soit $\theta \in [0,\pi]$, il nous est possible de trouver une partie $S \subset \{1,\ldots, n\}$ (qui sera simplement les indices des vecteurs contenus dans un « bon » secteur d'angle $2 \theta$) telle que \[ \left\| \sum_{i\in S} \vec v_i \right\| \geq \frac \theta \pi \,\cos \theta.\]

On a alors répondu à la question, pour peu qu'on soit capable de montrer que la fonction $\frac{\theta \, \cos \theta }\pi $ atteigne sur $[0, \pi /2]$ au moins une valeur $\geq \frac 1 \pi$. On s'en convainc aisément par une étude numérique de la fonction (mais la valeur maximale, à peu près égale à $0,1786$, n'a pas d'expression simple) ou par tâtonnement. Par exemple, on obtient en $\theta = \pi /4$ la valeur \[ \frac 1 \pi \, \frac{\pi} 4 \, \frac{\sqrt 2}2 = \frac{\sqrt{2}}8 > \frac 1 6.\]

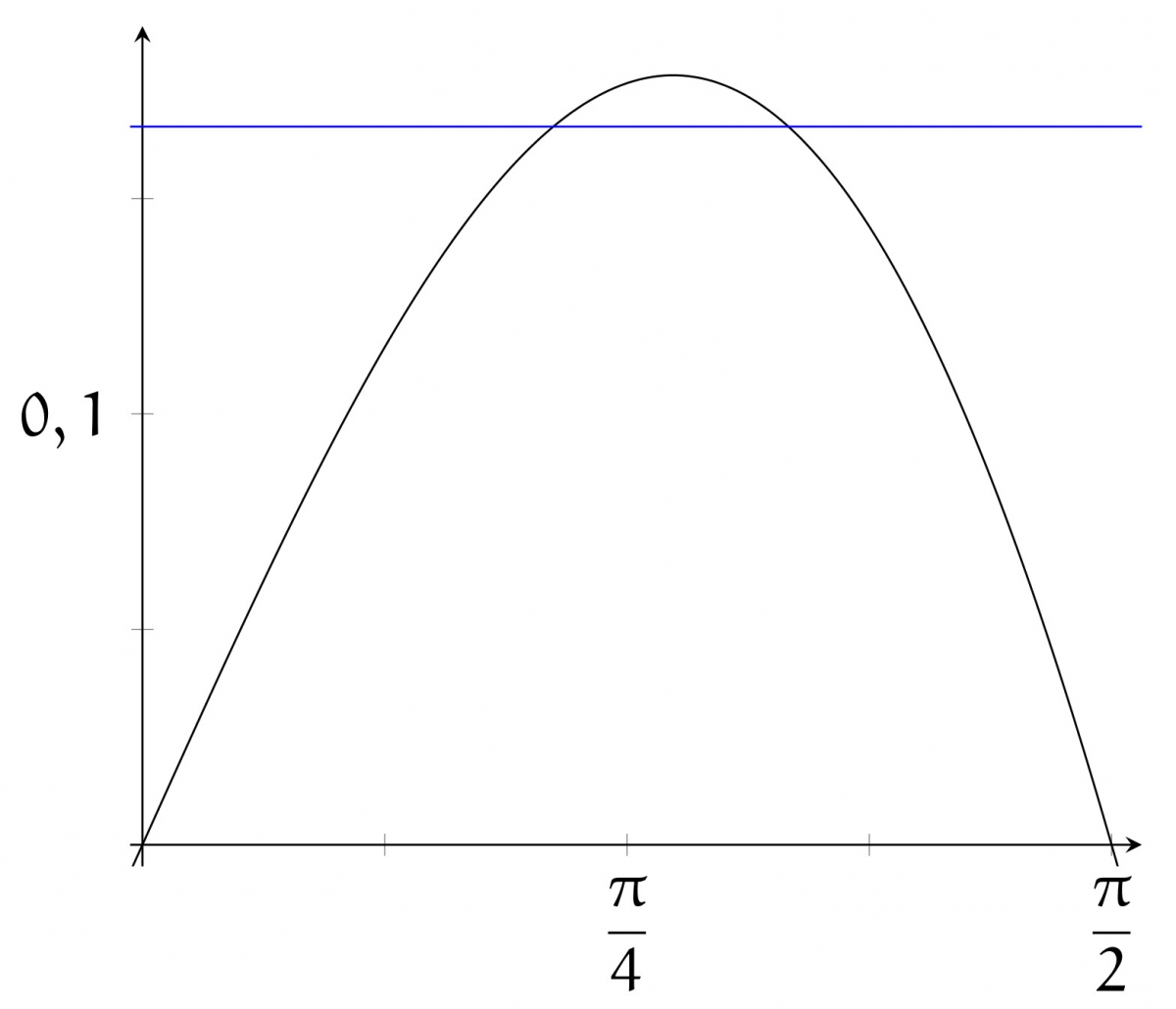
Graphe de $\theta \mapsto \frac{\theta\,\cos\theta}{\pi}$.