L'algorithme d'Euclide

Cet article est disponible au format pdf.

 

Sommaire

A. PGCD et algorithme d'Euclide (3e)

1. Divisibilité

Définition. Soit $a, b$ deux entiers naturels. On dit que $a$ divise $b$ s'il existe un entier naturel $q$ tel que $b = aq$.
On dit aussi que $a$ est un diviseur de $b$, que $b$ est un multiple de $a$ ou que $b$ est divisible par $a$...

Exemples.

On rappelle les principaux critères de divisibilité. Ceux-ci sont démontrés en annexe à la fin de l'article.

Critères de divisibilité.

Exercice. À chaque période de circulation alternée, une (petite) polémique éclate sur les nombres se terminant par $0$ : sont-ils pairs ? sont-ils ni pairs, ni impairs ? Que dire du nombre $0$ lui-même ?

Solution. Les nombres se terminant par $0$ sont pairs d'après le critère de divisibilité ci-dessus. Cela est d'ailleurs assez facile à démontrer : on sait que multiplier un nombre par $10$ revient à ajouter un zéro à droite dans son écriture décimale. Autrement dit, les nombres se terminant par un $0$ sont les nombres de la forme $10 \times n$. Puisque $10 = 2 \times 5$, le nombre $10 \times n = 2 \times (5 \times n)$ est bien un multiple de $2$ : il est pair.

En particulier, le nombre $0$ est bien sûr pair : $0 = 2 \times 0$.

Exercice. Trouver un nombre plus grand que $1$ qui divise $123\,456\,789$.

Solution. On voit que $1+2+3+4+5+6+7+8+9 = 45$, qui est un multiple de $9$. D'après le critère de divisibilité, $123\,456\,789$ est divisible par $9$ (et donc par $3$).

2. Nombres premiers

Cette notion de diviseurs permet des distinctions dans l'ensemble de tous les nombres entiers. La figure suivante illustre par exemple le nombre de diviseursLa fonction associant à un entier $n$ le nombre de ses diviseurs est suffisamment importante pour avoir un nom en arithmétique : on la note souvent $n \mapsto \tau(n)$. La suite $(\tau(n))$, dont on donne ici les premières valeurs, est la suite A000005 de l'Online Encyclopedia of Integer Sequences. de tous les entiers compris entre $1$ et $100$. On a écrit (un peu arbitrairement) 42 $\!\vdash\!$ 8 pour dire que 42 a huit diviseurs.

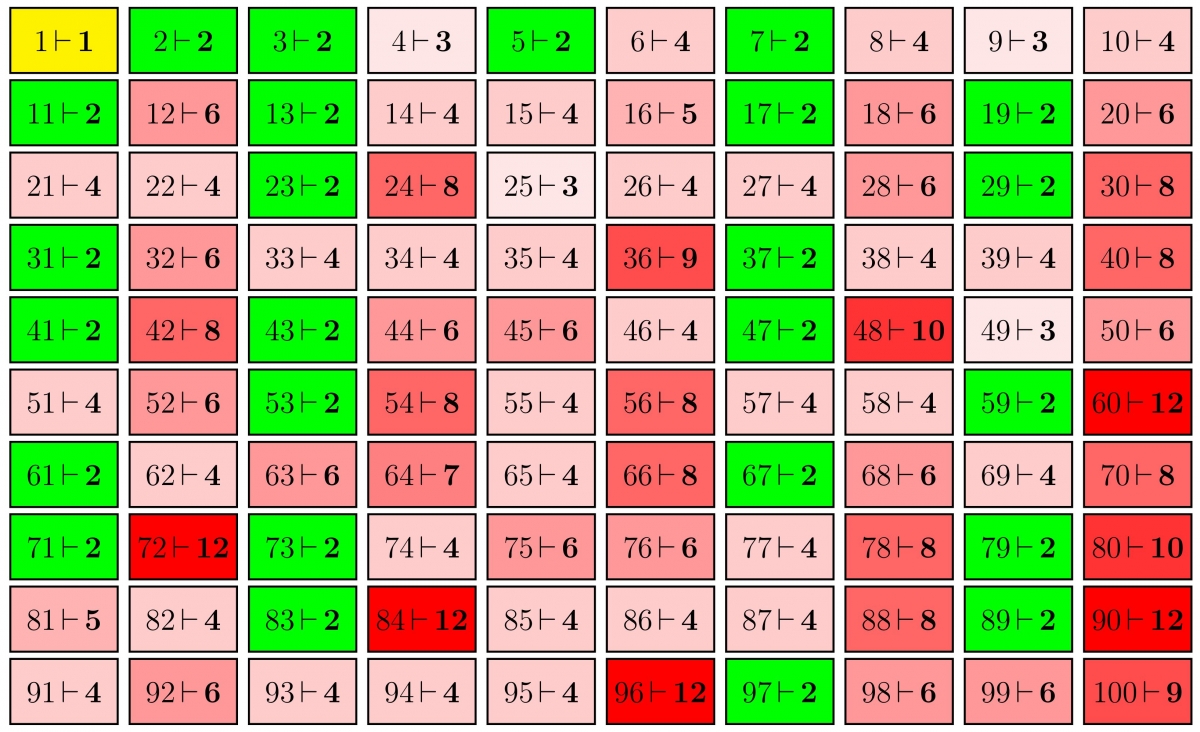
On remarque que $1$ est le seul nombre à n'avoir qu'un seul diviseur. En effet, si un nombre est plus grand que $1$, il a automatiquement au moins deux diviseurs : $1$ et lui-même.

À part cette petite remarque, on voit que les comportements sont très différents d'un nombre à l'autre et que des nombres ayant beaucoup de diviseurs (comme $60$, qui en a douze : $1$, $2$, $3$, $4$, $5$, $6$, $10$, $12$, $15$, $20$, $30$ et $60$) cotoient des nombres en ayant très peu (comme $61$, qui n'en a que deux). Les nombres de cette dernière catégorie sont d'une importance fondamentale en arithmétique.

Définition. Un entier naturel est premier s'il possède exactement deux diviseurs : $1$ et lui-même.

Exemples.

Euclide est un mathématicien grec dont la vie nous est pratiquement inconnue. Les treize livres de ses Éléments constituent une sorte d'encyclopédie du savoir mathématique de son temps. On pourra consulter cet article de Bernard Vitrac pour plus d'informations à son sujet. affirme que l'ensemble des nombres premiers est infini. On donne en annexe à la fin de ce document trois preuves de ce théorème.

Exercice. Quelqu'un digne de confiance vous affirme que parmi les neuf nombres compris entre $524\,282$ et $524\,290$, il y a un nombre premier. Identifiez-le.

Solution. On peut déjà éliminer tous les nombres pairs et $524\,285$ qui, se terminant par un $5$, est un multiple de $5$. Il reste alors $524\,283$, $524\,287$ et $524\,289$. En calculant la somme de leurs chiffres, on voit que les deux extrêmes sont des multiples de $3$ ($524\,289$ est même divisible par $9$). Ainsi, seul $524\,287$ peut être premier (et il l'est effectivement).

3. Plus grand commun diviseur (PGCD)

Définition. Soit $a, b \geq 0$ deux entiers naturels. Le PGCD (plus grand commun diviseur) de $a$ et $b$ est le plus grand des entiers naturels $k$ qui divisent à la fois $a$ et $b$. On le note $\mathrm{pgcd}(a,b)$.

Exemple. Calculons le PGCD de $12$ et $15$. On peut systématiquement lister leurs diviseurs :

Seuls $1$ et $3$ divisent donc à la fois $12$ et $15$ : leur PGCD vaut $3$.

Remarques.

Exemples.

Exercice. Calculer le PGCD de $67$ et de $100$.

Solution. $67$ est un nombre premier (on peut par exemple le voir dans la liste donnée plus haut). Ses seuls diviseurs sont $1$ et $67$. Comme $100$ n'est pas un multiple de $67$, leur PGCD ne peut être que $1$.

Exercice. Calculer le PGCD de $9$ et de $111\,111\,111\,111$.

Solution. Les diviseurs de $9$ sont $1$, $3$ et $9$. On peut alors chercher à appliquer les critères de divisibilité pour voir si $111\,111\,111\,111$ est divisible par $3$ et $9$ (il est de toute façon divisible par $1$). Le somme des chiffres de ce grand nombre vaut $12$. Comme $12$ est un multiple de $3$, $111\,111\,111\,111$ l'est aussi. Comme $12$ n'est pas un multiple de $9$, $111\,111\,111\,111$ non plus. Les diviseurs communs à $9$ et à $111\,111\,111\,111$ sont donc simplement $1$ et $3$, ce qui entraîne que leur PGCD vaut $3$.

Exercice. Calculer le PGCD de $48$ et de $60$.

Solution. Alors que ces nombres sont beaucoup moins grands que $111\,111\,111\,111$, leur grand nombre de diviseurs va compliquer les choses. Avec un peu de courage, on peut déterminer les listes de diviseurs suivantes :

Leurs diviseurs communs sont donc $1$, $2$, $3$, $4$, $6$ et $12$. Leur PGCD est donc $12$. Cet exemple illustre bien que déterminer les listes complètes de diviseurs n'est pas une solution très satisfaisante en général pour déterminer le PGCD. C'est le rôle que va remplir l'algorithme d'Euclide.

Exercice. On souhaite colorier une grille en regroupant les cases en carrés tous de la même taille mais de couleur différente. Voici par exemple une solution pour une grille de taille $9 \times 6$ :

Quel est le nombre minimal de couleurs nécessaires pour colorier de la sorte une grille $16 \times 12$ ?

Solution. On voit sur la figure que la taille du côté du carré divise à la fois la hauteur et la largeur de la grille. Pour utiliser le moins de couleurs possible, il faut utiliser un carré le plus grand possible. Ainsi, il s'agit de calculer le PGCD de $12$ et $16$. On peut vérifier que les diviseurs de $12$ sont $1$, $2$, $3$, $4$, $6$, $12$ et ceux de $16$ sont $1$, $2$, $4$, $8$ et $16$. Ainsi, le PGCD vaut $4$. En regroupant les grilles en carrés $4 \times 4$, on voit qu'il faudra alors $\frac {16}4 \times \frac {12}4 = 4 \times 3 = 12$ couleurs.

Définition. Soit $a, b \geq 1$ deux entiers. On dit que $a$ et $b$ sont premiers entre eux. si le seul entier les divisant tous les deux est $1$. Par définition, cela équivaut au fait que leur PGCD vaut $1$.

L'exercice suivant peut être vu comme une première justification de cette terminologie.

Exercice. Soit $p$ et $q$ deux nombres premiers. À quelle condition $p$ et $q$ sont-ils premiers entre eux ?

Solution. Si $p = q$, le PGCD de $p$ et $q$ est évidemment $p$ lui-même. En revanche, si $p$ est différent de $q$, les diviseurs de $p$ sont $1$ et $p$ alors que ceux de $q$ sont $1$ et $q$. Comme seul $1$ est commun à ces deux listes, $p$ et $q$ sont premiers entre eux.

Exercice. Soit $p$ un nombre premier et $1 \leq n < p$ un nombre entier. Montrer que $n$ et $p$ sont premiers entre eux.

Solution. Les seuls diviseurs de $p$ sont $1$ et $p$. Puisque $n < p$, ce nombre n'est pas un multiple de $p$. Autrement dit, le seul diviseur de $p$ qui divise $n$ est $1$. Ces nombres sont donc premiers entre eux.

4. Algorithme d'Euclide

L'idée sous-jacente à l'algorithme d'Euclide est le résultat suivant.

Proposition. Soit $a \geq b \geq 1$ deux nombres entiers. Alors les diviseurs communs à $a$ et $b$ sont exactement les diviseurs communs à $a - b$ et $b$. En particulierRemarquons que si $a = b$, on retrouve bien le cas particulier $\mathrm{pgcd}(0,a) = a$ mentionné plus haut., \[ \mathrm{pgcd}(a,b) = \mathrm{pgcd}(a-b,b).\]

Démonstration. Supposons que $k$ divise à la fois $a$ et $b$. Cela signifie que l'on peut trouver des entiers $u$ et $v$ tels que $a = ku$ et $b=kv$. En particulier, \[ a - b = ku - kv = k(u-v),\] donc ce nombre est également divisible par $k$. Ainsi, si un nombre divise à la fois $a$ et $b$, il divise à la fois $a-b$ et $b$.

Réciproquement, si $k$ divise à la fois $b$ et $a-b$, on peut trouver des entiers $v$ et $w$ tels que $a = kv$ et $a-b = kw$. On a alors \[ b = b + (a-b) = kv + kw = k(u+w),\] donc ce $b$ est également divisible par $k$. Ainsi, si un nombre divise à la fois $a-b$ et $b$, il divise à la fois $a$ et $b$ et on a démontré la première partie du résultat.

La deuxième partie s'en déduit immédiatement : on vient de voir que les diviseurs communs à $a$ et $b$ étaient exactement les mêmes que les diviseurs communs à $a-b$ et $b$. En particulier, le plus grand de ces diviseurs communs doit être le même, c'est-à-dire \[ \mathrm{pgcd}(a,b) = \mathrm{pgcd}(a-b,b).\]

On peut déjà utiliser ce résultat « à la main » pour calculer des PGCD plus vite qu'en listant tous les diviseurs. Par exemple, si l'on souhaite calculer le pgcd de $225$ et $60$, on peut réaliser la suite d'opérations suivante : \begin{align*} \mathrm{pgcd}(225, 60) &\stackrel != \mathrm{pgcd}(225-60, 60) = \mathrm{pgcd}(165, 60) \\ &\stackrel != \mathrm{pgcd}(165-60,60) = \mathrm{pgcd}(105,60)\\ &\stackrel != \mathrm{pgcd}(105-60, 60) = \mathrm{pgcd}(45, 60) = \mathrm{pgcd}(60,45)\\ &\stackrel != \mathrm{pgcd}(60 - 45, 45) = \mathrm{pgcd}(15, 45)\\ &= 15, \end{align*} où l'on a utilisé intensivement (à chaque fois que l'égalité est surmontée d'un $!$) le résultat ci-dessus. Remarquons que l'on a arrêté le calcul à $\mathrm{pgcd}(15,45) = 15$ parce que l'on a noté que $15$ était un diviseur de $45$, mais que l'on aurait pu continuer à appliquer la méthode pour obtenir successivement $\mathrm{pgcd}(45,15) = \mathrm{pgcd}(30, 15) = \mathrm{pgcd}(15, 15) = 15$ sans devoir faire preuve d'aucune astuce.

La méthode est donc complètement générale et peut être vue comme une espèce de précurseur de l'algorithme d'Euclide. On l'appelle parfois algorithme soustractif.

Exercice. Utiliser l'algorithme soustractif pour calculer le pgcd de $168$ et $300$.

Solution. On applique mécaniquement la méthode : \begin{align*} \mathrm{pgcd}(300,168) &= \mathrm{pgcd}(168, 132)\\ &= \mathrm{pgcd}(132, 36) \\ &= \mathrm{pgcd}(96, 36)\\ &= \mathrm{pgcd}(60, 36) \\ &= \mathrm{pgcd}(36, 24)\\ &= \mathrm{pgcd}(24,12)\\ &= 12. \end{align*}

Exercice. Soit $n \geq 1$ un nombre entier. Quel est le PGCD de $n$ et $n+1$ ? Quel est le PGCD de $n$ et $n+2$ ?

Solution. En appliquant la proposition ci-dessus, on voit que $\mathrm{pgcd}(n+1,n) = \mathrm{pgcd}(n,1)$. Or, $1$ est le seul diviseur de $1$ (et il divise également $n$), donc ce PGCD vaut $1$. Autrement dit, les entiers $n$ et $n+1$ sont premiers entre eux.

De la même façon, $\mathrm{pgcd}(n+2, n) = \mathrm{pgcd}(n,2)$. Les diviseurs de $2$ sont $1$ et $2$. Le nombre $1$ divise automatiquement $n$, mais il n'en va pas forcément de même de $2$. En fait, il faut distinguer les cas : si $n$ est pair, c'est un multiple de $2$ et le PGCD est donc $2$. En revanche, si $n$ est impair, $1$ est le seul diviseur commun à $2$ et $n$ donc le PGCD vaut $1$.

On voit que ces arguments s'appliquent de la même façon dans un cas plus général : si $p$ est un nombre premier, le PGCD de $n$ et $n+p$ vaut $p$ si $n$ est un multiple de $p$, et $1$ sinon.

Imaginons que nous devions calculer le PGCD de $1\,024\,001$ et $1\,026\,001$. À la première étape, l'algorithme soustractif simplifie pas mal les choses : \[ \mathrm{pgcd}(1\,026\,001, 1\,024\,001) = \mathrm{pgcd}(1\,024\,001, 2\,000).\] Cependant, l'idée de soustraire de façon répétée $2\,000$ à $1\,024\,001$ est peu réjouissante. Elle l'est d'autant moins que l'on peut prévoir ce qui se passera : on va enlever $512$ fois $2\,000$ à $1\,024\,001$ pour obtenir \[1\,024\,001 \underbrace{- 2\,000 - \cdots - 2\,000}_{\text{$512$ fois}} = 1\,024\,001 - 512 \times 2\,000 = 1.\]

Autrement dit, au bout de ces $512$ étapes pénibles, l'algorithme soustractif arrivera au calcul de $\mathrm{pgcd}(2\,000,1)$, qui vaut évidemment $1$.

Analysons de plus près ce que nous avons fait : l'égalité $1\,024\,001 = 512 \times 2\,000 + 1$ permet de prédire le comportement de l'algorithme soustractif : il va appliquer $512$ fois la proposition que nous avons démontrée pour arriver à \begin{eqnarray*} \mathrm{pgcd}(1\,024\,001, 2\,000) &=& \mathrm{pgcd}(1\,022\,001, 2\,000)\\ &=& \cdots\\ &=& \mathrm{pgcd}(2\,001,2\,000)\\ &=& \mathrm{pgcd}(1,2\,000) = 1. \end{eqnarray*}

L'égalité $1\,024\,001 = 512 \times 2\,000 + 1$ permet donc de court-circuiter l'algorithme soustractif pour calculer le PGCD plus vite : elle nous permet d'affirmer que \[ \mathrm{pgcd}(1\,024\,001, 2\,000) = \mathrm{pgcd}(1,2\,000).\] Pour reformuler encore une fois, on peut utiliser la « division » pour accélérer l'algorithme soustractif. En effet, l'égalité $1\,024\,001 = 512 \times 2\,000 + 1$ est une manière d'exprimer le résultat obtenu quand on pose la division :

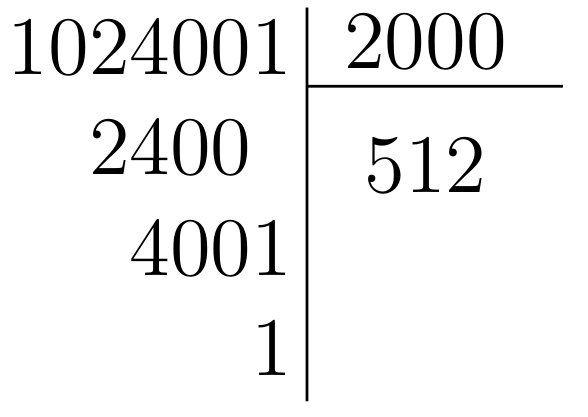
L'algorithme d'Euclide est donc une amélioration de l'algorithme soustractif où l'on utilise, au lieu de la proposition déjà énoncée, la version plus forte :

Proposition. Soit $a$ et $b$ deux nombres entiers, avec $a > b$. Si on note $q$ et $r$ le quotient et le reste obtenus en posant la division de $a$ par $b$ (c'est-à-dire que $a = bq + r$, avec $r < b$), on a l'égalité \[ \mathrm{pgcd}(a,b) = \mathrm{pgcd}(b,r).\]

Pour démontrer cette proposition, on peut soit remarquer qu'elle s'obtient en appliquant $q$ fois la proposition initiale, soit imiter la preuve de cette dernière (en notant que $r = a - bq$).

L'algorithme d'Euclide consiste alors à calculer le PGCD de deux nombres en appliquant cette proposition de façon répétée.

Exemple. On reprend l'exemple de $225$ et de $60$. On cherche à calculer $d = \mathrm{pgcd}(225,60)$. \begin{align*} 225 &= 3 \times 60 + 45 && \text{donc } d=\mathrm{pgcd}(60,45)\\ 60 &= 1 \times 45 + 15 && \text{donc } d = \mathrm{pgcd}(45,15)\\ 45 &= 3 \times 15 && \text{donc } d= 15. \end{align*} Dans la dernière étape, on a constaté que la division « tombait juste » et donc que $15$ divisait $45$, ce qui entraîne que $\mathrm{pgcd}(45,15) = 15$.

Exercice. Calculer le PGCD de $2211$ et de $100$.

Solution. Soit $d = \mathrm{pgcd}(2211,100)$. \begin{align*} 2211 &= 22 \times 100 + 11 && \text{donc } d=\mathrm{pgcd}(100,11)\\ 100 &= 9 \times 11 + 1 && \text{donc } d = \mathrm{pgcd}(11,1) = 1. \end{align*}

Exercice. On vient de faire cuire $20\,160$ brocolis et $6\,048$ pommes de terre. On souhaite les utiliser pour constituer le plus grand nombre de plateaux-repas possibles, en respectant deux règles : dans un souci d'équité, les plateaux-repas doivent tous contenir exactement le même nombre de brocolis et le même nombre de pommes de terre ; et pour éviter le gaspillage, les brocolis et les pommes de terre doivent tous être distribués. Quel est le nombre maximum de plateaux-repas que l'on peut constituer ?

Solution. Si l'on met $b$ brocolis et $p$ pommes de terre sur chaque plateau-repas, le nombre $n$ de tels plateaux vérifie les relations $20\,160 = n \times b$ et $6\,048 = n \times p$. Autrement dit, le nombre de plateaux est un diviseur commun de $20\,160$ et $6\,048$. Puisqu'on veut que $n$ soit le plus grand possible, calculons leur PGCD $d = \mathrm{pgcd}(20\,160, 6\,048)$ : \begin{align*} 20\,160 &= 3 \times 6\,048 + 2\,016 && \text{donc } d = \mathrm{pgcd}(6\,048, 2\,016)\\ 6\,048 &= 3 \times 2\,016 && \text{donc } d = 2\,016. \end{align*} Au maximum, on pourra donc distribuer $2\,016$ plateaux-repas (qui contiendront donc $10$ brocolis et $3$ pommes de terre chacun).

B. Programmation de l'algorithme d'Euclide (2de)

Comme son nom l'indique, l'algorithme d'Euclide est un algorithme, c'est-à-dire une suite d'opérations précises aboutissant au calcul du PGCD. On va ici expliciter complètement l'algorithme, puis l'implémenter dans le langage de programmation Algobox.

Comme on l'a vu, l'idée de l'algorithme d'Euclide est que si $a = bq + r$ est le résultat de la division de $a$ par $b$ (avec $a \geq b$), le PGCD de $a$ et $b$ est égal à celui de $b$ et $r$. Quand on a à calculer $\mathrm{pgcd}(a,b)$, on va donc trouver $q$ et $r$. Il peut alors se passer deux choses :

L'idée est donc de faire cette opération de discussion jusqu'à tomber sur $r = 0$. Autrement dit, on va faire une boucle dans laquelle on restera tant que $r \neq 0$. On peut donc écrire une première version (encore un peu floue) de notre algorithme.

Cet algorithme renvoie toujours une solution après un nombre fini d'étapes. En effet, à chaque étape, le plus grand des deux nombres $a$ et $b$ a diminué. Comme il est impossible pour un entier naturel de diminuer indéfiniment, cela démontre que l'algorithme ne peut pas tourner infiniment longtemps sans produire de réponse.

Voyons comment coder cet algorithme avec Algobox. Évidemment, Algobox dispose d'une boucle TANT_QUE, que nous pourrons utiliser. Attention toutefois à bien définir $r$ avant de rentrer dans la boucle.

Comment faire la division de $a$ par $b$ avec Algobox ? Quand on écrit $a = bq + r$, avec $r < b$, on a $\frac ab = q + \frac rb$, avec $\frac rb < 1$. Autrement dit, le $q$ n'est rien d'autre que la partie entière de la fraction $\frac ab$ (qui donne en général un nombre non entier). La fonction partie entière d'Algobox s'appelle floor. On pourra donc définir $q$ par la commande : q PREND_LA_VALEUR floor(a/b), du moins si $a$ est plus grand que $b$.

Cette commande floor nous sera d'ailleurs utile pour vérifier que les nombres entrés par l'utilisateur sont bien des entiers. En effet, si $a$ n'est pas entier, il est différent de sa partie entière. Ainsi une condition comme SI (a!=floor(a) OU a<=0) sera vérifiée si $a$ n'est pas un entier ou qu'il est négatif ou nul. On pourra donc dans ce cas afficher un message d'erreur à l'utilisateur.

Pour calculer $r$ une fois que l'on a calculé $q$, on pourrait simplement utiliser la formule $r = a - bq$. En fait, le nombre obtenu comme reste dans la division de $a$ par $b$ est une quantité tellement importante que la plupart des langages de programmation (et en particulier Algobox) disposent d'une fonction pour le calculer directement. Dans Algobox, cette fonction est notée par le symbole %. On pourra donc simplement calculer $r$ par la commande r PREND_LA_VALEUR a%b.

Il nous reste une petite subtilité à régler : quand on pose la division, on cherche à diviser le plus grand des nombres $a$ et $b$ par le plus petit. En fait, le seul problème peut se poser à cause de l'ordre dans lequel l'utilisateur entre les nombres. En effet, quand on fait la division $a = bq + r$, $r$ est automatiquement plus petit que $b$. Puisque l'algorithme utilise alors $b$ et $r$ à la place de $a$ et $b$, ces deux nombres sont déjà rangés dans le bon ordre. Ainsi, les nombres $a$ et $b$ seront toujours rangés dans le bon ordre, à part peut-être à la première exécution de la boucle, suivant l'ordre dans lequel l'utilisateur les a donnés. On commence donc le calcul avec $a = \max(x,y)$ et $b = \min(x,y)$, où $x$ et $y$ sont les valeurs rentrées par l'utilisateur.

Ainsi, une version minimale de notre boucle (une fois $a$ et $b$ définis, et avec une valeur initiale de $r$ différente de $0$ pour que l'on rentre effectivement dans la boucle) pourrait s'écrire :

Que faire une fois que l'on est sorti de cette boucle ? Si l'on en est sorti, c'est que r vaut finalement $0$. Ainsi, le dernier calcul a donné que la division de a par b tombait juste. Le PGCD est donc simplement la valeur prise par b à ce moment du calcul. Or, dans les deux lignes suivantes, les valeurs sont réattribuées : la valeur de b qui nous intéressait est affectée à la variable a alors que la valeur de r (dont elle sait qu'elle vaut 0) est affectée à la variable b. Ainsi, une fois sorti de la boucle, la valeur du PGCD est celle qui est stockée dans la variable a.

En ajoutant des messages pour montrer les calculs intermédiaires, voilà donc le code source final.

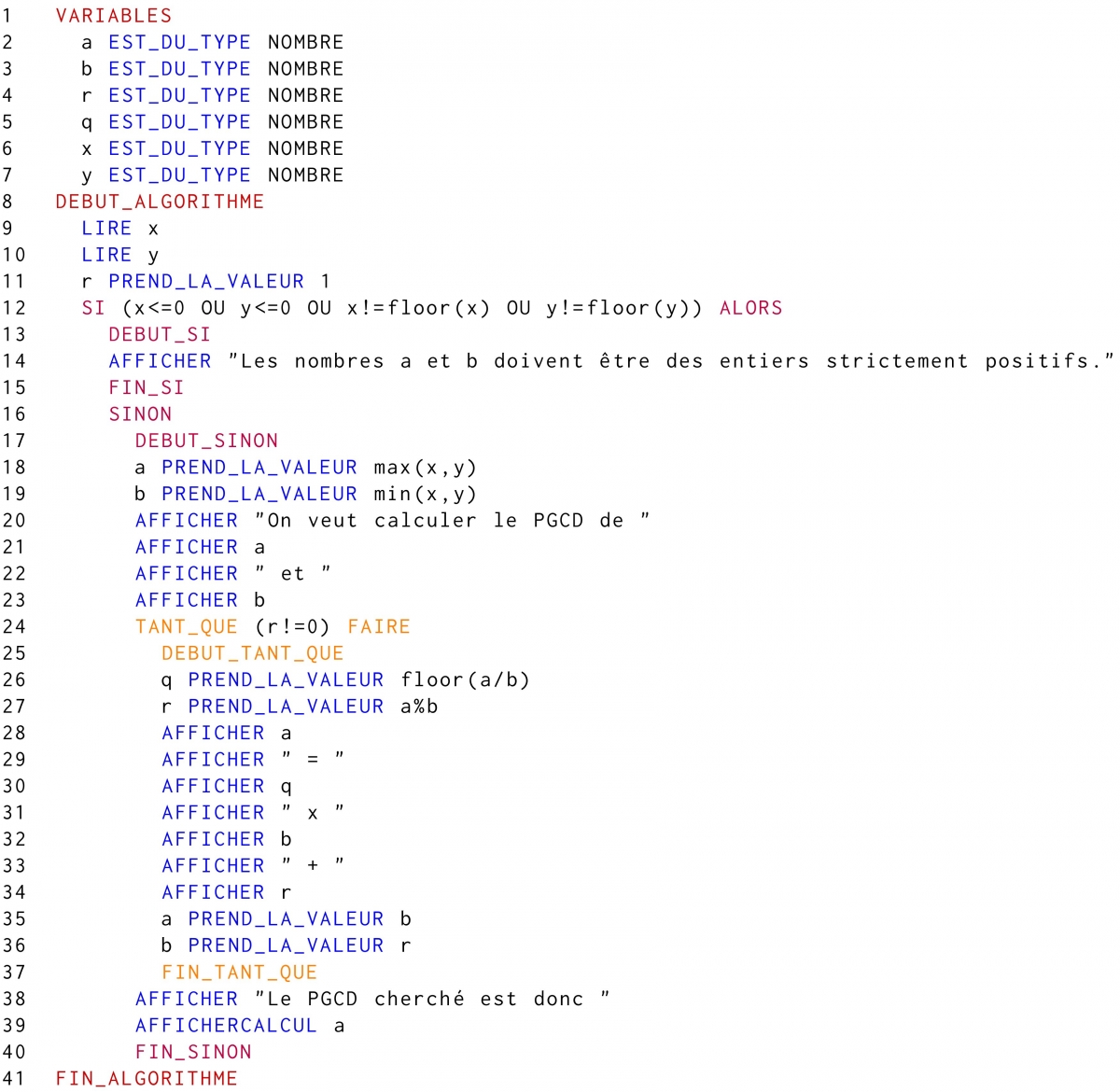
Remarque. On s'est ici attaché à afficher les étapes intermédiaires du calcul, pour coller au plus près de la description de l'algorithme d'Euclide « à la main » que nous avons expliqué plus tôt. Cependant, on peut voir par exemple que le quotient $q$ n'intervient jamais dans les calculs. Il serait donc possible de gagner du temps en ne le calculant pas du tout. De même, il n'est pas forcément très important de faire attention à l'ordre entre $a$ et $b$ : si on cherche à faire la division euclidienne de $a$ par $b$ alors que $a \leq b$, on va tomber sur la division un peu bête $a = 0 \times b + a$. Au prochain tour de calcul, l'algorithme repartira donc avec $b$ et $a$, c'est-à-dire qu'il les aura en quelque sorte « remis dans le bon ordre. » Un programme plus court (mais n'indiquant pas les étapes de calcul) pourrait donc être le suivant.

C. Théorème de Bézout et conséquences (TS, spécialité)

1. Deux calculs

Exercice. Combien de chiffres a le plus grand nombre premier connu $p = 2^{57\,885\,161}-1$ ?

Solution. Les nombres premiers de la formeUn exercice classique d'arithmétique consiste à montrer que si un nombre de la forme $a^m - 1$ est premier, alors $a = 2$ et $m$ est un nombre premier. Cela repose sur l'égalité $q^m - 1 = (q - 1)(q^{m-1} + \cdots + q^2 + q + 1)$. $2^n - 1$ sont appelés nombres de Mersenne. Il existe en fait des algorithmes assez efficaces pour déterminer si un nombre de cette forme est premier ou non, ce qui a pour conséquence que le plus grand nombre premier connu est quasiment toujours un nombre de Mersenne.

Pour aborder cet exercice, rappelons que la fonction logarithme en base 10, définie par la formule $\log_{10}(x) = \frac{\ln(x)}{\ln(10)}$ est manifestement une fonction strictement croissante telle que $\log_{10}(10^m) = m$.

En outre, $p$ et $2^{57\,885\,161}$ ont le même nombre de chiffres (si ce n'était pas le cas, $p$ s'écrirait $9999\cdots 9999$, et serait évidemment divisible par $9$, ce qui est absurde). Comme $10^r$ est le plus petit nombre à $r+1$ chiffres, on cherche l'entier $r$ tel que \[ 10^{r-1} \leq 2^{57\,885\,161} < 10^{r}.\]

En passant cette inégalité au logarithme en base $10$, on obtient \[ r - 1 \leq \log_{10}\left(2^{57\,885\,161}\right) < r.\] ou encore \[ r - 1 \leq 57\,885\,161 \times \frac{\ln 2}{\ln 10} < r.\]

Ainsi, comme $57\,885\,161 \times \frac{\ln 2}{\ln 10} \approx 17\,425\,169,76$, le plus grand nombre premier connu a $17\,425\,170$ chiffres.

Exercice. Les nombres de Fibonacci sont définis par récurrence par les formules : \[ F_1 = F_2 = 1 \qquad \text{et} \qquad F_{n+2} = F_{n+1} + F_n.\] Par exemple, $F_3 = 1 + 1 = 2$, $F_4 = 1 + 2 = 3$, $F_5 = 2 + 3 = 5$, etc. Soit $n \geq 1$ un nombre entier. Montrer que $F_n$ et $F_{n+1}$ sont premiers entre eux.

Solution. Remarquons que la suite $F_n$ est croissante (et même strictement croissante à partir de $n = 2$). Ainsi, la définition $F_{n+2} = F_{n+1} + F_n$ ou, mieux, l'égalité \[ F_{n+2} = 1 \cdot F_{n+1} + F_n\] exprime que $F_n$ est le reste de la division de $F_{n+2}$ par $F_{n+1}$. En particulier, si on pose $d = \mathrm{pgcd}(F_{n+1},F_n)$, l'algorithme d'Euclide donne \begin{align*} F_{n+1} &= F_n + F_{n-1} && \text{donc } d = \mathrm{pgcd}(F_n, F_{n-1})\\ F_{n} &= F_{n-1} + F_{n-2} && \text{donc } d = \mathrm{pgcd}(F_{n-2}, F_{n-3}), \end{align*} et ainsi de suite... On a donc \begin{eqnarray*} \mathrm{pgcd}(F_{n+1}, F_n) = \cdots &=& \mathrm{pgcd}(F_3,F_2)\\ & =& \mathrm{pgcd}(F_2,F_1) = \mathrm{pgcd}(1,1) = 1. \end{eqnarray*}

Remarque. Avec un peu plus de soin, on peut même démontrer la jolie formule \[ \mathrm{pgcd}(F_n, F_m) = F_{\mathrm{pgcd}(n,m)}.\]

2. Théorème de Bézout

Le théorème de BézoutÉtienne Bézout (1730-1783) est un mathématicien français. En sus du théorème que nous présentons ici, son nom reste attaché à un important théorème de géométrie algébrique comptant les points d'intersection de deux courbes définies par des équations polynomiales. est une propriété importante du PGCD de deux entiers, même si elle peut être un peu surprenante au premier abord. Avant de l'énoncé, commençons par étendre la définition de la divisibilité aux entiers relatifs.

Définition. Soit $a$ et $b$ des entiers relatifs. On dit que $a$ divise $b$ s'il existe un entier relatif $k$ tel que $b = ak$.

Exemples. Puisque l'on peut multiplier par $-1$, les multiples de $a$ et de $-a$ sont toujours les mêmes : si $b = ak$, on a aussi $b = (-a) (-k)$. De la même façon, les diviseurs de $a$ et de $-a$ sont également les mêmes.

Remarque. Pour ne pas modifier la définition de nombres premiers, on demande alors qu'un nombre premier soit un entier naturel ayant exactement $2$ diviseurs positifs : $1$ et lui-même.

Théorème de Bézout. Soit $a$ et $b$ deux entiers non nuls et $d = \mathrm{pgcd}(a,b)$. On peut alors trouver $u$ et $v$ dans $\mathbb{Z}$ tels que $au + bv = d$.

Corollaire. Soit $k$ un entier divisant à la fois $a$ et $b$. Alors $k$ divise $\mathrm{pgcd}(a,b)$.

Démonstration du corollaire. Si $k$ divise $a$, on peut trouver un entier $r$ tel que $a = kr$. De même, on peut trouver un entier $s$ tel que $b=ks$. On a alors, d'après le théorème de Bézout, \[ d = au+bv = kru + ksv = k(ru+sv).\] qui est bien un multiple de $k$.

Remarque (importante). Ce corollaire a pour conséquence que l'on peut changer la définition du PGCD. Dans la première section de ce document, nous l'avions défini comme le plus grand des diviseurs communs pour l'ordre usuel, c'est-à-dire le diviseur commun qui était supérieur à tous les autres. On voit ici qu'il s'agit également du plus grand diviseur commun en un sens plus fort, puisqu'il est en fait un multiple de tous les autres.

Remarque. Cette redéfinition du PGCD (le PGCD de $a$ et $b$ est l'unique diviseur de $a$ et $b$ qui est un multiple de tous les autres) rend naturelle la convention $\mathrm{pgcd}(0,0) = 0$ que nous avons formulée plus haut. En effet, tous les nombres entiers (y compris $0$) sont des diviseurs de $0$. Comme $0$ est un multiple de tous les nombres entiers, on retrouve bien dans ce cas $\mathrm{pgcd}(0,0) = 0$.

Exercice. On distribue $21\,700$ bonbons et $10\,900$ stylos à un groupe de personnes. Après une distribution équitable, il reste $69$ bonbons et $36$ stylos non attribués. Combien y a-t-il de personnes dans le groupe ?

Solution. L'énoncé entraîne que le nombre de personnes dans le groupe divise à la fois $21\,700 - 69 = 21\,631$ et $10\,900 - 36 = 10\,864$. En particulier, il divise leur PGCD $d = \mathrm{pgcd}(21\,631,10\,864)$. Calculons-le. \begin{align*} 21\,631 &= 1 \times 10\,864 + 10\,767 && \text{donc } d = \mathrm{pgcd}(10\,837,10\,767)\\ 10\,864 &= 1 \times 10\,767 + 97 && \text{donc } d = \mathrm{pgcd}(10\,767, 97)\\ 10\,767 &= 111 \times 97 && \text{donc } d = 97. \end{align*}

Or, $97$ est un nombre premier. Les diviseurs de $97$ (qui sont les diviseurs communs à $21\,631$ et à $10\,900$) sont donc $1$ et $97$. Comme il serait curieux de désigner une personne seule comme « un groupe de personnes », on en déduit qu'il y a $97$ personnes.

Démonstration du théorème de Bézout. Considérons l'ensemble $E \subset \mathbb{Z}$ des entiers pouvant s'écrire sous la forme $au+bv$, pour des $u$ et $v$ bien choisis. En particulier, l'ensemble $E$ contient les multiples $au$ de $a$ (qui correspondent au cas $v = 0$) et les multiples de $v$.

On veut démontrer que $d$ appartient à cet ensemble.

Soit $\delta > 0$ le plus petit entier strictement positif appartenant à $E$. (Il en existe, puisque soit $a$ soit $-a$ est positif et appartient à $E$). Par définition, on peut trouver des entiers $u$ et $v$ tels que $\delta = a u + bv$. On va en fait montrer que $\delta = d$.

Montrons d'abord que $E$ est exactement l'ensemble des multiples de $\delta$. Déjà, tout multiple $k \delta = k(au+bv) = a(ku) + b(kv)$ appartient bien à $E$.

Réciproquement, prenons $m$ un élément de $E$. En posant la division de $m$ par $\delta$, on trouve deux entiers $q$ et $0 \leq r < \delta$ tels que $m = q \delta + r$. Cela entraîne que $r \in E$. En effet, si $u'$ et $v'$ sont des entiers tels que $m = au'+bv'$, on a \[ r = m - q \delta = (au'+bv') - q (au+bv) = a (u'-qu) + b (v' - qv) \in E.\]

Mais on a supposé que $\delta$ était le plus petit entier strictement positif dans $E$, et on a vu que $0 \leq r < \delta$. La seule possibilité est donc que $r = 0$, et $m$ est donc bien un multiple de $\delta$.

En particulier, puisque $a$ et $b$ appartiennent à $E$, ce sont eux aussi des multiples de $\delta$. Ce nombre est donc bien un diviseur commun de $a$ et $b$. Montrons que c'est le plus grand. Soit donc $d' \geq 1$ un diviseur commun de $a$ et $b$. On peut donc trouver deux entiers $k$ et $l$ tels $a = kd'$ et $b=ld'$. On a alors \[ \delta = a u + b v = kd'\,u + ld'\,v = (ku+lv)d',\] ce qui montre que $\delta$ est un multiple de $d'$. En particulier, $\delta \geq d'$. On a donc bien montré que $\delta = d$, ce qui montre que $d \in E$.

Remarques.

3. Algorithme d'Euclide et théorème de Bézout

L'algorithme d'Euclide permet de rendre concret le théorème de Bézout. Plus exactement, si $d$ est le pgcd de $a$ et $b$, on peut « remonter » l'algorithme d'Euclide pour trouver une relation de Bézout $d = au + bv$.

Exemple. On cherche à trouver une relation de Bézout entre $225$ et $60$. Rappelons l'algorithme d'Euclide permettant de calculer $d = \mathrm{pgcd}(225,60)$. \begin{align*} 225 &= 3 \times 60 + 45 && \text{donc } d=\mathrm{pgcd}(60,45)\\ 60 &= 1 \times 45 + 15 && \text{donc } d = \mathrm{pgcd}(45,15)\\ 45 &= 3 \times 15 && \text{donc } d= 15. \end{align*}

On voit alors qu'on peut remonter l'algorithme pour trouver des relations de Bézout entre les différents nombres intervenants. La dernière division permettait de passer du calcul de $\mathrm{pgcd}(60,45)$ au calcul « évident » $\mathrm{pgcd}(45, 15) = 15$ (car $15$ est un multiple de $45$). En effet, la division de $60$ par $45$ donnait \[ 60 = 1 \times 45 + 15,\] que l'on peut réécrire \[ 15 = 1 \times 60 - 1 \times 45,\] ce qui est bien une relation de Bézout entre $60$ et $45$.

En passant à la ligne supérieure, on voit que l'on peut remplacer le $45$ intermédiaire par quelque chose faisant intervenir $225$ et $60$. On en déduit \begin{align*} 15 &= 1 \times 60 - 1 \times (225 - 3 \times 60)\\ &= 4 \times 60 - 1 \times 225, \end{align*} ce qui est bien une relation de Bézout.

Exercice. Trouver $u$ et $v$ tels que $2016 \times u + 299 \times v = 1$.

On applique d'abord l'algorithme d'Euclide pour trouver $d = \mathrm{pgcd}(2016, 299)$. \begin{align*} 2016 &= 6 \times 299 + 222 &&\text{donc } d = \mathrm{pgcd}(299,222)\\ 299 &= 1 \times 222 + 77 && \text{donc } d = \mathrm{pgcd}(222,77)\\ 222 &= 2 \times 77 + 68 && \text{donc } d = \mathrm{pgcd}(77,68)\\ 77 &= 1 \times 68 + 9 && \text{donc } d = \mathrm{pgcd}(68,9)\\ 68 &= 7 \times 9 + 5 && \text{donc } d = \mathrm{pgcd}(9,5)\\ 9 &= 1 \times 5 + 4 && \text{donc } d=\mathrm{pgcd}(5,4)\\ 5 &= 1\times 4 + 1 && \text{donc } d = \mathrm{pgcd}(4,1)=1. \end{align*}

Enfin ! Ces deux nombres sont donc premiers entre eux. On peut alors remonter l'algorithme pour trouver une relation de Bézout. Remarquez que l'on trouve en fait des relations de Bézout pour chacun des couples intermédiaires qui sont apparus au cours de l'algorithme.

\begin{align*} (5,4) && 1 &= 1 \times 5 - 1 \times 4\\ (9,5) && 1 &= 1 \times 5 - 1 \times (9 - 1 \times 5)\\ &&1 &= 2 \times 5 - 1 \times 9\\ (98,9) &&1& = 2 \times (68 - 7 \times 9) - 1 \times 9\\ &&1&= 2 \times 68 - 15 \times 9\\ (77,68) && 1 &= 2 \times 68 - 15 \times (77 - 1 \times 68)\\ && 1&= 17 \times 68 - 15 \times 77\\ (222,77) && 1&= 17 \times (222 - 2 \times 77) - 15 \times 77\\ && 1 &= 17 \times 222 - 49 \times 77\\ (299, 222)&& 1 &= 17 \times 222 - 49 \times (299 - 1 \times 222)\\ && 1&= 66 \times 222 - 49 \times 299\\ (2016,299) && 1 &= 66 \times (2016 - 6 \times 299) - 49 \times 299\\ && 1 &= 66 \times 2016 - 445 \times 299, \end{align*} qui est bien une relation de la forme désirée.

Exercice. « Mon équipe a perdu, mais seulement de quatre points. » Une telle déclaration est-elle envisageable au rugby ? au quidditch ? De manière plus générale quels sont les écarts possibles dans chacun de ces deux sports ? On rappelle qu'au rugby, une action peut rapporter $3$ points (drop-goal ou pénalité), $5$ points (essai non transformé) ou $7$ points (essai transformé), alors qu'au quidditch, une action peut rapporter $10$ points (but) ou $150$ points (capture du vif d'orPour cet exercice, on oublie que la capture du vif d'or est une action qui ne peut se produire qu'une fois par match...). Même question pour un sport imaginaire où les actions A at B rapporteraient $28$ et $16$ points, respectivement.

Solution. La déclaration est tout à fait envisageable au rubgy (l'équipe pourrait n'avoir marqué qu'une pénalité, contre un essai transformé de l'adversaire, pour un score de $3$ à $7$) mais elle ne l'est pas au quidditch où tous les scores, et donc tous les écarts de scores sont des multiples de $10$.

Plus généralement, tous les écarts sont possibles au rugby : la relation de Bézout $7 - 2 \times 3 = 1$, par exemple, assure que si l'équipe $A$ marque $n$ essais transformés alors que l'équipe $B$ marque $2n$ pénalités, l'écart sera de $n$ points. De même au quidditch, on voit directement que tous les multiples de $10$ sont possibles.

Pour le sport imaginaire, calculons le PGCD $d = \mathrm{pgcd}(28,16)$ et déterminons une relation de Bézout. \begin{align*} 28 &= 1 \times 16 + 12 && \text{donc } d = \mathrm{pgcd}(16,12)\\ 16 &= 1 \times 12 + 4 && \text{donc } d = \mathrm{pgcd}(12, 4) = 4. \end{align*}

\begin{align*} (16,12) && 4 &= 16 - 1 \times 12 \\ (28, 16) && 4 &= 16 - 1 \times (28 - 1 \times 16)\\ && 4 &= 2 \times 16 - 1 \times 28. \end{align*} Ainsi, tous les scores sont des multiples de $4$, et il en va de même des écarts de scores. Réciproquement, si l'on veut un écart de $4n = 2n \times 16 - n \times 28$, il suffit qu'une des équipes ait marqué $2n$ fois avec l'action A, alors que l'autre n'a marqué que $n$ fois, avec l'action B.

4. Conséquences du théorème de Bézout

Malgré sa forme peut-être un peu surprenante, le théorème de Bézout permet de démontrer facilement des théorèmes arithmétiques importants.

Proposition. Si un nombre $n$ est divisible par $a$ et par $b$ et que ces deux nombres sont premiers entre eux, il est divisible par $ab$.

Démonstration. D'après les hypothèses, on peut trouver des entiers $k$ et $l$ tels que $n = ak$ et $n = bl$. De plus, d'après le théorème de Bézout, on peut trouver $u$ et $v$ tels que $au+bv=1$. On a alors \[ n = 1 \times n = (au+bv) n = au\times n + bv\times n = au\times bl + bv \times ak = ab\times (ul+vk),\] qui est bien divisible par $ab$.

Exercice. Comment reconnaître facilement qu'un nombre est un multiple de $45$ ? Par exemple, est-ce que $4\,685\,368\,545$ est un multiple de $45$ ?

Solution. D'après les critères de divisibilité, il est facile de vérifier qu'un nombre est un multiple de $9$ et de $5$ : il faut que la somme de ses chiffres soit un multiple de $9$ et que son dernier chiffre soit un $5$ ou un $0$. Mais, d'après ce que l'on vient de dire, si un nombre est divisible par $9$ et par $5$, il est divisible par $9 \times 5 = 45$ (car $9$ et $5$ sont premiers entre eux). En particulier, la somme des chiffres de $4\,685\,368\,545$ valant $54 = 6 \times 9$, ce nombre est divisible par $45$.

Lemme de Gauss.Carl Friedrich Gauss (1777-1855) est un mathématicien allemand dont les travaux couvrent la totalité des mathématiques de son époque. Son livre Disquisitiones arithmeticae a notamment complètement révolutionné l'arithmétique. Soit $a$, $b$ et $c$ trois nombres entiers tels que $a$ divise $bc$. Si $a$ est premier avec $b$, alors $a$ divise $c$.

Démonstration. On écrit une relation de Bézout pour $a$ et $b$ : il existe des entiers $u$ et $v$ tels que $au+bv = 1$. La relation de divisibilité indique qu'il existe un entier $k$ tel que $ak = bc$. On a alors \[ akv = bcv = c \times bv = c(1-au) = c - acu,\] ce que l'on peut réécrire $c = a(cu+kv)$, ce qui montre que $c$ est un multiple de $a$.

Corollaire (lemme d'Euclide). Soit $p$ un nombre premier et $b$ et $c$ deux nombres entiers tels que $p$ divise $bc$. Alors $p$ divise $b$ ou $p$ divise $c$.

Démonstration. En effet, les diviseurs de $p$ étant $1$ et $p$, le PGCD de $p$ et $b$ est aussi $1$ ou $p$. Dans le premier cas, $p$ et $b$ sont premiers entre eux et le lemme de Gauss s'applique (donc $p$ divise $c$). Dans le second, $p$ divise $b$.

Les deux lemmes précédents sont des outils efficaces pour démontrer le théorème de décomposition en nombres premiers, aussi parfois appelé le théorème fondamental de l'arithmétique. Nous ne démontrerons pas ce théorème ici mais en donnerons deux conséquences revenant sur les points abordés au début du document.

Théorème de factorisation en nombres premiers. Soit $n$ un entier différent de $0$, $1$ et $-1$. Il existe alors un nombre $\epsilon \in \{\pm 1\}$, des nombres premiers distincts $p_1 < \ldots < p_r$ et des nombres entiers $v_1, \ldots, v_r \geq 1$ tels que \[ n = \epsilon p_1^{v_1} \cdots p_r^{v_r}.\] De plus, cette décomposition est unique : si on a $\epsilon p_1^{v_1} \cdots p_r^{v_r} = \eta q_1^{v_1} \cdots q_s^{v_s}$, avec $\eta \in \{\pm 1\}$, $q_1 < \cdots < q_s$ des nombres premiers et $w_1, \ldots, w_s \geq 1$ des entiers, alors $\epsilon = \eta$, $r = s$ et pour tout $i$ compris entre $1$ et $r$, $p_i = q_i$ et $v_i = w_i$.

Remarques.

Exemples.

En guise d'application du théorème de factorisation, revenons sur le PGCD et sur le nombre de diviseurs d'un entier. Soit donc $n \geq 1$ un entier. D'après le théorème, on peut le factoriser sous la forme $n = p_1 ^{v_1} \cdots p_r^{v_r}$. Que dire de ses diviseurs ?

Quand on fait le produit de deux nombres, on a vu que les nombres premiers qui apparaissent sont ceux qui interviennent dans la décomposition de l'un des deux facteurs (voire dans les deux). Les exposants restent alors les mêmes pour les premiers n'apparaissant que dans l'un des facteurs, et ils s'ajoutent si le nombre premier intervient dans les deux. Cela a pour conséquence que les diviseurs d'un nombre décomposé en facteurs premiers sont faciles à décrire.

Proposition. Soit $n = p_1 ^{v_1} \cdots p_r^{v_r}$ un nombre entier, avec $v_1, \ldots, v_r \geq 1$. Les diviseurs de $n$ sont alors les nombres de la forme $p_1^{w_1} \cdots p_r^{w_r}$, où l'on a $0 \leq w_1 \leq v_1$, $0\leq w_2 \leq v_2, \ldots, 0\leq w_r \leq v_r$.

En particulier, cette proposition permet de compter les diviseurs d'un nombre. Pour chaque nombre premier $p_i$ le divisant, correspondant à la puissance $v_i$, on doit choisir un nombre $0 \leq w_i \leq v_i$. Il y a donc $v_i+1$ choix. Autrement dit, le nombre de diviseurs de $n = p_1 ^{v_1} \cdots p_r^{v_r}$ est le produit \[ \tau(n) = (v_1 +1) \cdots (v_r+1).\] En particulier, si un nombre est une puissance $p^v$ d'un nombre premier, il a $v+1$ diviseurs. S'il est un produit $p_1\cdots p_r$ de nombres premiers distincts, il en a $2^r$. On peut vérifier ces relations sur la table des premières valeurs de $\tau(n)$ donnée au début du document.

Cette caractérisation permet également de calculer le PGCD de deux nombres : si $n_1 = p_1^{v_1} \cdots p_r^{v_r}$ et $n_2 = p_1^{w_1} \cdots p_r^{w_r}$ (ici, on écrit $n_1$ et $n_2$ avec les mêmes nombres premiers, quitte à autoriser les entiers $v_i$ et $w_i$ à s'annuler). Vu la forme des diviseurs donnée plus haut, on voit que les diviseurs communs à $n_1$ et $n_2$ sont les \[ k = p_1^{\nu_1} \cdots p_r^{\nu_r},\] où, pour tout $i$, $\nu_i$ est inférieur (ou égal) à $v_i$ et $w_i$ simultanément. En particulier, \[ \mathrm{pgcd}(n_1, n_2) = p_1^{\min(v_1, w_1)} \cdots p_r^{\min(v_r,w_r)}.\]

Par exemple, comme $48 = 2^4 \times 3$ et $60 = 2^2 \times 3 \times 5$, on retrouve \[ \mathrm{pgcd}(48,60) = 2^2 \times 3^1 \times 5^0 = 12.\]

5. Deux mondes sans factorisation unique

Le théorème de factorisation en nombres premiers est tellement central en arithmétique qu'il est difficile d'imaginer s'en passer. Pour conclure cet article, nous allons signaler deux situations (dont l'une seule est sérieuse) où il ne va pourtant pas de soi.

L'univers fun

On dira qu'un nombre est fun si son écriture en base 3 Finit par le chiffre UN, c'est-à-dire s'il est de la forme Le terme officiel pour cette notion serait plutôt celui de congru à $1$ modulo $3$. $3m+1$.

Dans un univers parallèle, une civilisation a développé ses mathématiques uniquement sur les nombres fun, au point que des notions comme le zéro ou le nombre $42$ sont complétement étrangères au système de pensée local.

Cette particularité a pour conséquence que l'addition a une structure différente dans l'univers fun. En effet, comme la somme de deux ou trois nombres fun n'est jamais fun, l'addition dans cet univers est une opération prenant quatre arguments et produisant une valeur (ce qui explique la forme du symbole), comme par exemple

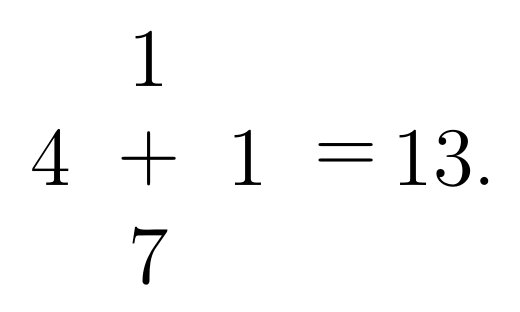
La multiplication ne pose pas les mêmes problèmes, puisqu'on vérifie facilement que le produit de deux nombres fun est toujours fun. Lors du développement de leur arithmétique, les mathématiciens fun ont naturellement dégagé la notion de nombre premier, c'est-à-dire de nombre fun ne se décomposant pas de façon non triviale en produit de deux nombres fun. Par exemple, $7$ est premier pour eux comme pour nous et $28 = 4 \times 7$ n'est premier ni pour eux ni pour nous. En revanche, $4$ est premier pour les mathématiciens fun, puisque le diviseur $2$, non fun, est invisible à leurs yeux.

Il est facile de montrer que, même avec leurs règles, tout nombre entier se décompose en facteurs premiers. En revanche, il n'y a pas unicité d'une telle décomposition. En effet, de même que $4$, il est facile de voir que $10$ et $25$ sont premiers au sens fun (car ni $2$ ni $5$ n'est fun). On a alors deux décompositions différentes \[ 100 = 10 \times 10 = 4 \times 25.\]

Pour pallier ce manque d'unicité, les mathématiciens fun auront peut-être l'idée d'introduire des nombres tout à fait artificiels, comme $2$ et $5$, pour rétablir au prix d'un ajout conceptuel l'unicité qui leur fait défaut.

L'anneau $\mathbb{Z}[i\sqrt 5]$

Retournons à des mathématiques terrestres. L'ensemble \[ A = \left\{a + b i\sqrt 5\,\middle|\, a, b \in \mathbb{Z}\right\}\] est un exemple d'anneau : il est stable par addition et par multiplication. On peut alors y calquer les notions usuelles d'arithmétique sur cet anneau. Un nombre $z \in A$ sera par exemple premierOn dit plutôt irréductible. s'il n'a pas de décomposition non triviale. Certains nombres entiers premiers le restent dans cet anneau (par exemple $2$ et $3$, mais il faudrait le démontrer), alors que certains se scindent en un produit non trivial, comme \[ 29 = 3^2 + 5\times 2^2 = (3 + i\sqrt 5)(3 - i \sqrt 5).\]

De même que dans l'exemple précédent, on peut alors vérifier qu'il est toujours possible de décomposer un nombre en produit d'irréductibles, mais on est alors confronté à un problème de non-unicité. Par exemple, on peut montrer que les deux écritures \[ 6 = 2 \times 3 = (1 + i\sqrt 5)(1 - i \sqrt 5)\] sont des décompositions en irréductibles.

Contrairement à l'exemple précédent, cet anneau $A$ appartient à une classe de structures extrêmement importantes en arithmétique, et la non-unicité de la décomposition a des conséquences profondes sur l'étude de ces objets.Par exemple, le fait que la décomposition soit unique dans l'anneau $\mathbb{Z}[i] = \left\{a+ib\,\middle|\,a, b \in \mathbb{Z}\right\}$ permet de donner une démonstration conceptuelle (essentiellement due à Gauss) du théorème des deux carrés de Fermat. D'un autre côté, la « preuve », proposée en 1847 par Lamé à l'Académie des Sciences du grand théorème de Fermat était notamment fautive en ce qu'elle supposait l'unicité de la factorisation dans d'autres anneaux (les anneaux d'entiers cyclotomiques), pour lequels le résultat n'est pas valable (comme l'avait en fait montré Kummer trois ans auparavant). On pourra consulter [Edw75] pour en apprendre plus sur ce moment-clef de l'histoire de l'arithmétique. Il est possible de préserver un résultat d'unicité, au prix du remplacement de la notion élémentaire de nombre par celle d'idéaux de l'anneau $A$, qui est au cœur de la théorie algébrique des nombres. On trouvera par exemple une introduction à ces notions dans [IR90, chapitre 12] ou [Hin08, chapitre III, §.4]

Critères de divisibilité : les preuves

Critères de divisibilité par $2$ ou $5$

Ces critères sont probablement les plus simples : on peut reconnaître si un nombre est divisible par $2$ ou par $5$ en regardant simplement son dernier chiffre. Le point-clef est que la base que l'on emploie pour écrire les nombres, $10$, est un multiple de $2$ et de $5$.

Soit donc $n$ un nombre et $c$ son dernier chiffre (qui est donc un élément de $\{0,1,2,3,4,5,6,7,8,9\}$. Cela signifie que $n$ s'écrit $n = 10m + c$.

Ainsi, $n$ est divisible par $2$ si et seulement si $c$ l'est. En effet, si $c = 2d$, on a \[ n = 10m + 2d = 2 \times (5m + d).\] Réciproquement, si $n$ est divisible par $2$, on peut écrire $n = 2p$, et on a \[ c = n - 10 m = 2p - 10m = 2 \times (p - 5m).\]

Ainsi, un nombre est pair si et seulement si son dernier chiffre est divisible par $2$ (c'est-à-dire s'il s'agit de $0$, $2$, $4$, $6$ ou $8$).

La preuve marche exactement de la même façon pour la divisibilité par $5$. On obtient donc qu'un nombre est divisible par $5$ si et seulement si son dernier chiffre l'est (c'est-à-dire si son dernier chiffre est $0$ ou $5$).

Critère de divisibilité par $4$

De la même façon, on peut démontrer qu'un nombre est divisible par $4$ si et seulement si le nombre formé de ses deux derniers chiffres l'est. En formules, cela signifie que si $n = 100 m + c$, avec $0 \leq c \leq 99$, $n$ est divisible par $4$ si et seulement si $c$ l'est. La preuve de ce fait est très semblable aux preuves précédentes.

Si $c$ est divisible par $4$, on peut écrire $c = 4d$ et on a \[ n = 100 m + 4d = 4 \times (25m + d).\] Réciproquement, si $n$ est divisible par $4$, on peut écrire $n = 4p$, et on a \[ c = n - 100 m = 4p - 100 m = 4 \times (p-25m).\]

De même que le critère de divisibilité par $2$ allait de pairExercice. Admirer la beauté formelle de ce jeu de mots. avec son analogue pour $5$, le critère que l'on vient de montrer pour $4 = 2^2$ possède un analogue pour $25 = 5^2$, qui se démontre de façon tout à fait parallèle : \emph{un nombre est divisible par $ 25$ si et seulement si le nombre formé de ses deux derniers chiffres l'est.}

Pour aller encore plus loin, on peut remarquer que ces critères se généralisent à toutes les puissances de $2$ et de $5$ : un nombre est divisible par $625$ si et seulement si le nombre formé par ses quatre derniers chiffres l'est, un nombre est divisible par $65\,536$ si et seulement si le nombre formé par ses seize derniers chiffres l'est, etc.

Critères de divisibilité par $3$ et $9$

Les critères de divisibilité par $3$ et par $9$ se ressemblent manifestement. En fait, ils proviennent de la même propriété du nombre $10$ que nous utilisons comme base : quand on effectue la division de $10$ par $3$ (ou par $9$), on obtient un reste égal à $1$. Autrement dit, on a $10 = 3 \times 3 + 1$ et $10 = 1 \times 9 + 1$.

Démontrer ces critères demande des notations un peu plus lourdesOu un peu plus d'arithmétique, comme la notion de congruence.. Prenons donc un nombre $n$ et écrivons ses chiffres $c_0$, $c_1$, $c_2, \ldots, c_d$ (on numérote les chiffres de droite à gauche : $c_0$ est le chiffre des unités, $c_1$ est le chiffre des dizaines, etc.). En formules, cela signifie que \[ n = 10^d\, c_d + 10^{d-1}\,c_{d-1} + \cdots + 100\,c_2 + 10\,c_1 + c_0.\]

Remarquons que $10 = 3 \times 3 + 1$, $100 = 3 \times 33 + 1$, $1000 = 3 \times 333 + 1$ et, de manière générale, $10^k = 3 \times \xi_k + 1$, où $\xi_k$ est le nombre composé de $k$ chiffres « 3 ». Cette remarque permet de comparer $n$ et le nombre $c_d + c_{d-1} + \cdots + c_2 + c_1 + c_0$. En effet \begin{align*} n &= 10^d\, c_d + 10^{d-1}\,c_{d-1} + \cdots + 100\,c_2 + 10\,c_1 + c_0 \\ &= (3 \times \xi_d + 1) c_d + (3 \times \xi_{d-1} + 1) c_{d-1} + \cdots + (3 \times 33 + 1) c_2 + (3 \times 3 + 1) c_1 + c_0\\ &= \left(3 \xi_d c_d + 3 \xi_{d-1} c_{d-1} + \cdots + 3 \times 3 \times c_1\right) + \left(c_d + c_{d-1} + \cdots  c_1 + c_0\right)\\ &= 3\left(\xi_d c_d + \cdots + 33c_2 + 3 c_1\right) + \left(c_d + \cdots + c_2 + c_1 + c_0\right). \end{align*} On a donc démontré que la différence entre $n$ et la somme $c_d + \cdots + c_2 + c_1 + c_0$ de ses chiffres est un multiple de $3$. De même que dans les preuves des premiers critères, il est alors très facile de montrer que ces deux nombres sont soit tous les deux multiples de $3$, soit tous les deux non multiples de $3$. La preuve pour le critère de divisibilité par $9$ est exactement la même.

Il y a une infinité de nombres premiers : trois preuves

La preuve « originale »

La première des trois preuves que nous proposons est la plus proche de la preuve que l'on trouve dans les Éléments d'Euclide. Il s'agit en fait d'une « recette » expliquant comment, à partir d'un nombre fini de nombres premiers, on peut en construire un nouveau. Cela prouve bien qu'il en existe une infinité.

Soit donc $p_1, p_2, \ldots, p_r$ un nombre fini de nombres premiers. Considérons le nombre $N = p_1 p_2 \cdots p_r + 1$. Par construction, quand on effectue la division de ce nombre par l'un des $p_i$, on obtient un reste égal à 1. Ce nombre n'admet donc aucun des $p_i$ comme diviseur. Cependant, puisqu'il s'agit d'un nombre strictement plus grand que $1$, il doit avoir un diviseur premier $q$ (à cause du théorème de factorisation, par exemple, même si l'on n'en exploite pas toute la puissance). On a donc bien trouvé un nombre premier $q \not \in \{p_1, \ldots, p_r\}$.

Il y a trop de nombres entiers

La deuxième preuve que nous présentons est un peu étrange : nous allons supposer par l'absurde qu'il n'y a qu'un nombre fini de nombres premiers et voir que cela entraîne qu'il « manque » des entiers naturels.

En effet, remarquons une conséquence du théorème de factorisation en nombres premiers. Soit $n$ un entier naturel non nul. On peut l'écrire $n = p_1^{v_1}\cdots p_r^{v_r}$. Chacun de ces exposants $v_i$ est soit pair, soit impair. S'il est pair, on écrit $v_i = 2w_i$ ; sinon, $v_i = 2w_i +1$. Quitte à réordonner les nombres premiers, on va supposer que les exposants $v_1,\ldots, v_s$ sont impairs et les $v_{s+1}, \ldots, v_r$ sont pairs (cela permet simplement d'éviter des notations trop lourdes). On peut donc écrire \begin{align*} n &= p_1^{v_1}\cdots p_r^{v_r}\\ &= p_1^{2w_1+1}\cdots p_s^{2w_s+1} p_{s+1}^{2w_{s+1}} \cdots p_{r}^{2w_r}\\ &= \left(p_1^{w_1} \cdots p_s^{w_s} p_{s+1}^{w_{s+1}} \cdots p_r^{w_r}\right)^2 \times \left(p_1 \cdots p_s\right).\end{align*} Le deuxième facteur $p_1 \cdots p_s$ est un produit de nombres premiers tous différents. On peut facilement démontrer que cette propriété est équivalente au fait qu'aucun carré (à part $1$) ne divise le nombre. Pour cette raison, les entiers possédant cette propriété sont appelés sans facteur carré.On utilise parfois le terme allemand quadratfrei.

On a donc démontré que tout entier naturel est le produit d'un carré et d'un nombre sans facteur carré. On pourrait d'ailleurs démontrer que cette décomposition est unique, mais cela ne nous importe pas ici.

Évidemment, dans cette décomposition, les deux facteurs sont inférieurs ou égaux au nombre de départ. Autrement dit, on a démontré la proposition suivante.

Proposition. Tout entier compris entre $1$ et $N$ s'écrit comme le produit

Si un carré $r^2$ est inférieur à $N$, c'est que $r$ est inférieur à $\sqrt N$. Le nombre de carrés compris entre $1$ et $N$ est donc au plus $\sqrt N$.

C'est là que la preuve s'articule. Les entiers sans facteurs carrés sont les produits $q_1 \cdots q_l$ de nombres premiers tous différents. S'il n'y avait qu'un nombre fini de nombres premiers (disons $P$), il n'y aurait donc que $2^P$ entiers sans facteur carré (en effet, il y a autant d'entiers sans facteur carré que d'ensembles de nombres premiers tous différents).

D'après notre décomposition, les entiers entre $1$ et $N$ s'obtiendraient donc tous comme produit d'un carré inférieur ou égal à $N$ (et il y a au plus $\sqrt N$ choix) et d'un entier sans facteur carré (et il y a $2^P$ choix). On aurait donc \[ N = \left(\text{nombre d'entiers entre $1$ et $N$}\right) \leq 2^P \sqrt N,\] ce qui est absurde car nous savons que $N$ croît plus vite que tout multiple de $\sqrt N$.

Autrement dit, il ne peut pas y avoir seulement $P$ nombres premiers, car il n'y aurait alors pas plus de $2^P \sqrt N$ entiers entre $1$ et $N$.

Nombres de Fermat

Les nombres de Fermat $F_m = 2^{2^m} + 1$ ont une histoire intéressante. Ces entiers ont été découverts par Pierre de FermatMagistrat et mathématicien français du dix-septième siècle, Pierre de Fermat est sans doute connu principalement pour son célèbre « dernier théorème » affirmant que l'équation $x^n + y^n = z^n$ n'a pas, pour $n \geq 3$, de solutions entières non triviales, et qui ne fut en fait démontré qu'en 1994 par le mathématicien anglais (Sir) Andrew Wiles. Cela ne doit pas cacher l'étendue de l'œuvre mathématique de Fermat, qui est si importante que le mathématicien André Weil écrira en 1973 qu'il fut « l'une des personnalités mathématiques les plus fascinantes de tous les temps, le créateur (avec Descartes) de la géométrie analytique, un des fondateurs du calcul différentiel et le fondateur incontestable de l'arithmétique moderne. » qui remarqua que \[ F_0 = 3,\ F_1 = 5,\ F_2 = 17,\ F_3 = 257,\ \text{et} \ F_4 = 65\,537\] étaient tous premiers et conjectura un peu hardiment qu'il en allait de même des autres $F_m$.

Cette intuition est en fait fausse et Euler factorisera en 1732 le nombre de Fermat suivant, $F_5 = 4\,294\,967\,297 = 641 \times 6\,700\,417$. Pis, on ne connaît à l'heure actuelle aucun nombre de Fermat qui soit premier, à l'exception des cinq premiers découverts par Fermat lui-même (mais on n'exclut pas qu'une infinité d'entre eux le soit...) ! Les nombres premiers de Fermat, c'est-à-dire les $F_m$ qui sont effectivement premiers, sont également présents en géométrie, puisqu'on sait depuis les travaux de Gauss et Wantzel que si $p$ est un nombre premier, le polygone régulier à $p$ côtés n'est constructible à la règle et au compas que si $p$ est un nombre premier de Fermat.

Quoi qu'il en soit, les nombres de Fermat seront les acteurs de notre troisième preuve de l'existence d'une infinité de nombres premiers. Cela provient d'une égalité liant entre eux les nombres de Fermat.

Lemme. $F_0 F_1 \cdots F_m = 2^{2^m} - 1 = F_{m+1} - 2$.

Démonstration. Quand on développe le produit \[ F_0 F_1 \cdots F_m = \left(2^{2^0} + 1\right) \times \left(2^{2^1} + 1\right) \times \cdots \times \left(2^{2^m} + 1\right),\] chaque terme de la somme que l'on obtient a été obtenu en faisant le produit

Ce terme est donc égal à $2^k$, où $k$ est le nombre obtenu en ajoutant tous les $2^i$ correspondants aux termes où l'on a choisi de prendre $2^{2^i}$ plutôt que $1$. Autrement dit, le $i$-ème bit de l'écriture de $k$ en base $2$ est $1$ si l'on a choisi $2^{2^i}$ lors de notre $i$-ème décision, et $0$ sinon.

Ainsi, le produit développé fait intervenir $2^{m+1}$ nombres, égaux à $2^k$ où $k$ varie parmi l'ensemble de tous les nombres s'écrivant en base $2$ avec $m+1$ bits. Ces nombres forment l'intervalle $\{0, 1, \ldots, 2^{m+1} - 1\}$ et on en déduit donc \[ F_0 F_1 \cdots F_m = \sum_{k=0}^{2^{m+1} -1} 2^k = 2^{2^{m+1}} - 1 = F_{m+1} - 2.\]

Cette propriété a une conséquence importante : deux nombres de Fermat différents sont premiers entre eux. En effet, si $d$ divise $F_n$ et $F_m$, avec $n < m$, il divisera également $F_0 \cdots F_{m-1}$ (car $F_n$ apparaît comme un des facteurs) et divisera donc \[ 2 = F_{m+1} - F_0 F_1 \cdots F_m .\] Ainsi, le PGCD de $F_n$ et $F_m$ ne peut être que $1$ ou $2$. Comme ces nombres sont tous impairs, c'est nécessairement $1$ et $F_n$ et $F_m$ sont premiers entre eux.

Ainsi, si l'on choisit un des diviseurs premiers $p_i$ de $F_i$, on obtient fatalement une infinité de nombres premiers distincts.

Une dernière remarque

Les différentes preuves que nous avons données fournissent en fait des minorations de la fonction \[ \pi(x) = \left| \left\{ \text{nombres premiers} \ p \leq x \right\}\right|.\]

En lisant attentivement ces preuves, on peut en effet voir que la première et la troisième montrent l'inégalité \[ \pi(x) \geq \log_2 \left(\log_2 x)\right),\] alors que la deuxième montre l'inégalité plus forte \[\pi(x) \geq \frac 12 \log_2 x.\]

Un des couronnements du dix-neuvième siècle mathématique est le théorème des nombres premiers, démontré en 1896 par Hadamard et La Vallée Poussin (indépendamment), qui affirme que la fonction $\pi(x)$ est équivalente à $f(x) = \dfrac x{\ln x},$ c'est-à-dire que le rapport $\pi(x) / f(x)$ tend vers $1$ quand $x$ tend vers l'infini.

Références.