Vous pouvez retrouver cette question au format pdf.

Question du jeudi #25 : Vous êtes au centre d'une piscine circulaire, au bord de laquelle se trouve un lion. Est-il possible de sortir de la piscine en toute sécurité (c'est-à-dire d'arriver à un point du bord de la piscine où ne se trouve pas le lion), sachant que le lion se déplace quatre fois plus vite que vous ?

Remarquons déjà que la question ne dépend pas de la taille de la piscine ni de la vitesse des protagonistes (tant que celle du lion reste quatre fois plus grande que celle du nageur). Pour fixer les idées, on va donc prendre comme unité de distance le rayon de la piscine et comme unité de temps le temps qu'il faut au nageur pour parcourir ce rayon.

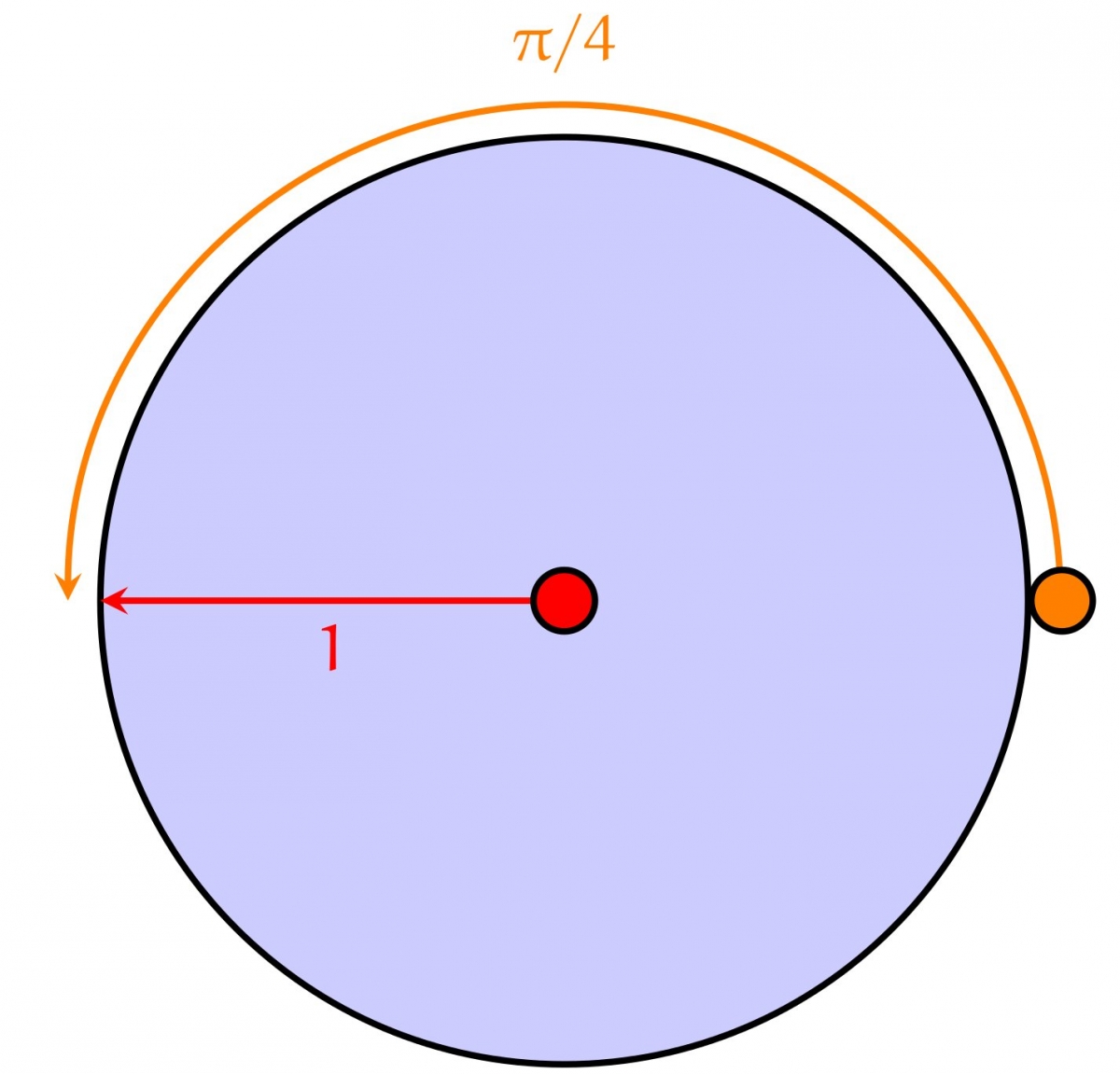
Commençons par remarquer que la solution la plus grossière ne marche pas. Si le nageur part en ligne droite dans la direction opposée à l'endroit où se trouve le lion, il lui faudra une unité de temps pour atteindre le bord, alors que le lion, qui doit parcourir un demi-périmètre de la piscine (c'est-à-dire $\pi$ fois la distance parcourue par le nageur), le fera en $\pi / 4  < 1$ unité de temps.



Cependant, le nageur a une solution pour « gagner du terrain » sur le lion. En effet, si le nageur tourne autour du centre de la piscine avec un rayon $r$ suffisamment petit (strictement inférieur au quart du rayon de la piscine),, le lion ne peut pas « le suivre » et rester au point du bord le plus proche du nageur. Par exemple, si le nageur tourne avec un rayon égal au cinquième du rayon de la piscine, la vitesse angulaire du lion sera $4/5$ fois la sienne.



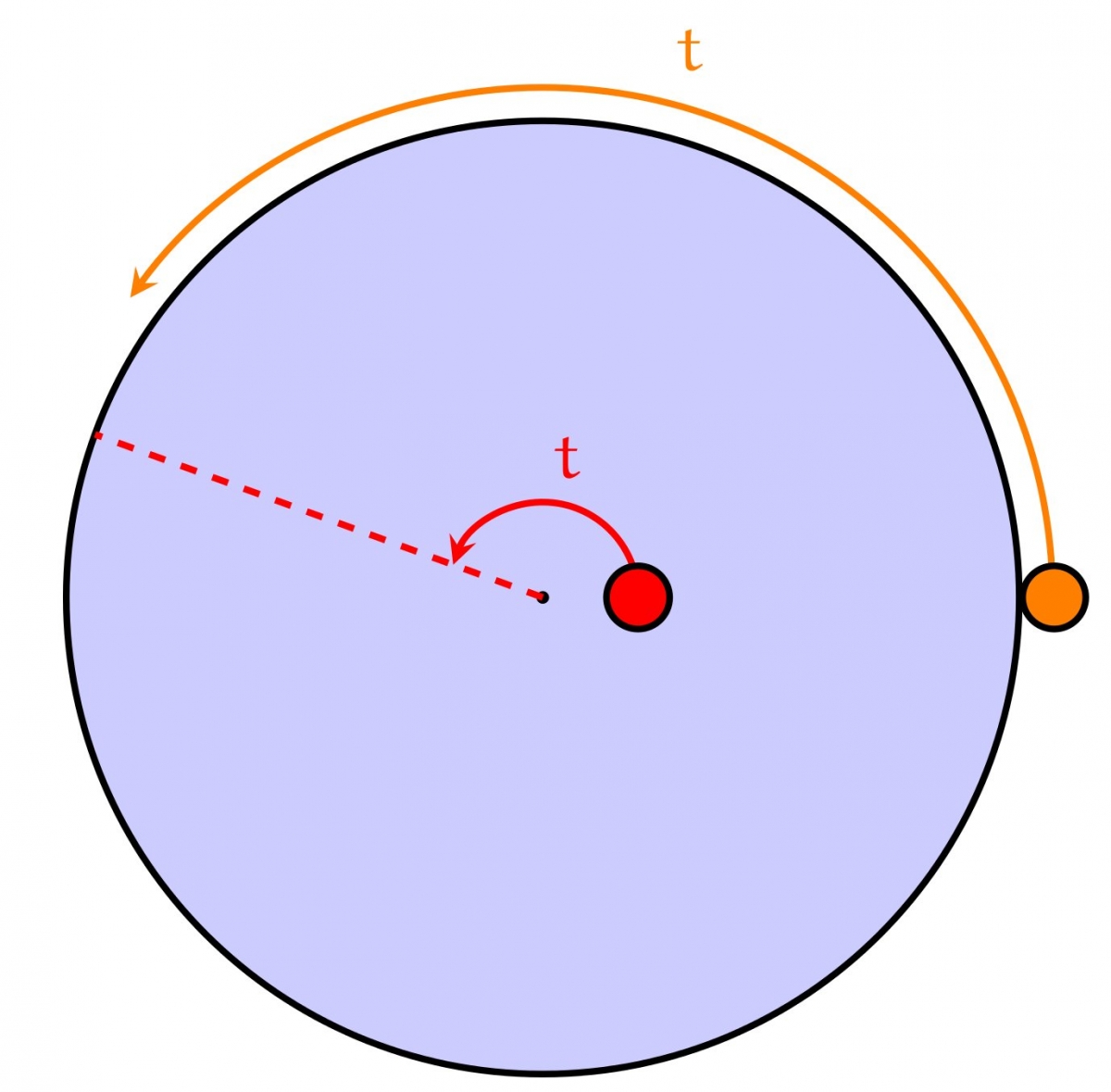
En particulier, en continuant à tourner avec un rayon $r$ strictement inférieur au quart de celui de la piscine, le nageur peut arriver dans une situation où le lion est au point du bord le plus éloigné de sa propre position. (Remarquons que la vitesse angulaire du nageur n'étant que $1/4r$ fois plus grande que celle du lion, cette étape prend un temps d'autant plus grand que $r$ est proche de $1/4$, en tout cas si le lion ne s'avoue pas vaincu et continue à « suivre » le nageur coûte que coûte).

On est donc arrivé à une situation meilleure qu'au départ : le nageur est un peu plus proche du bord (à distance $1-r$), et le lion est au point du bord le plus loin.

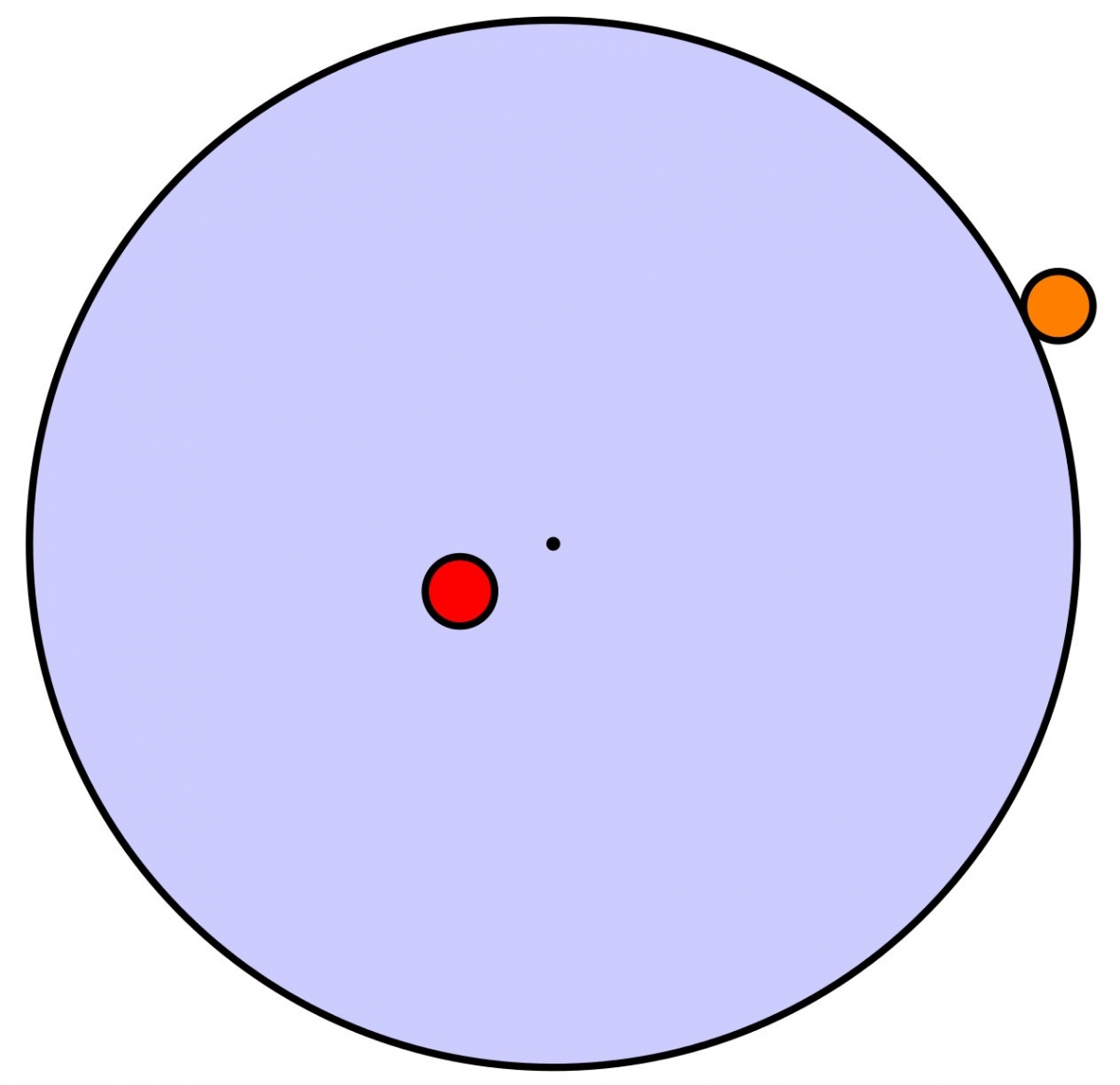
On peut alors retenter la méthode un peu naïve consistant à nager en ligne droite dans la direction opposée à celle du lion :

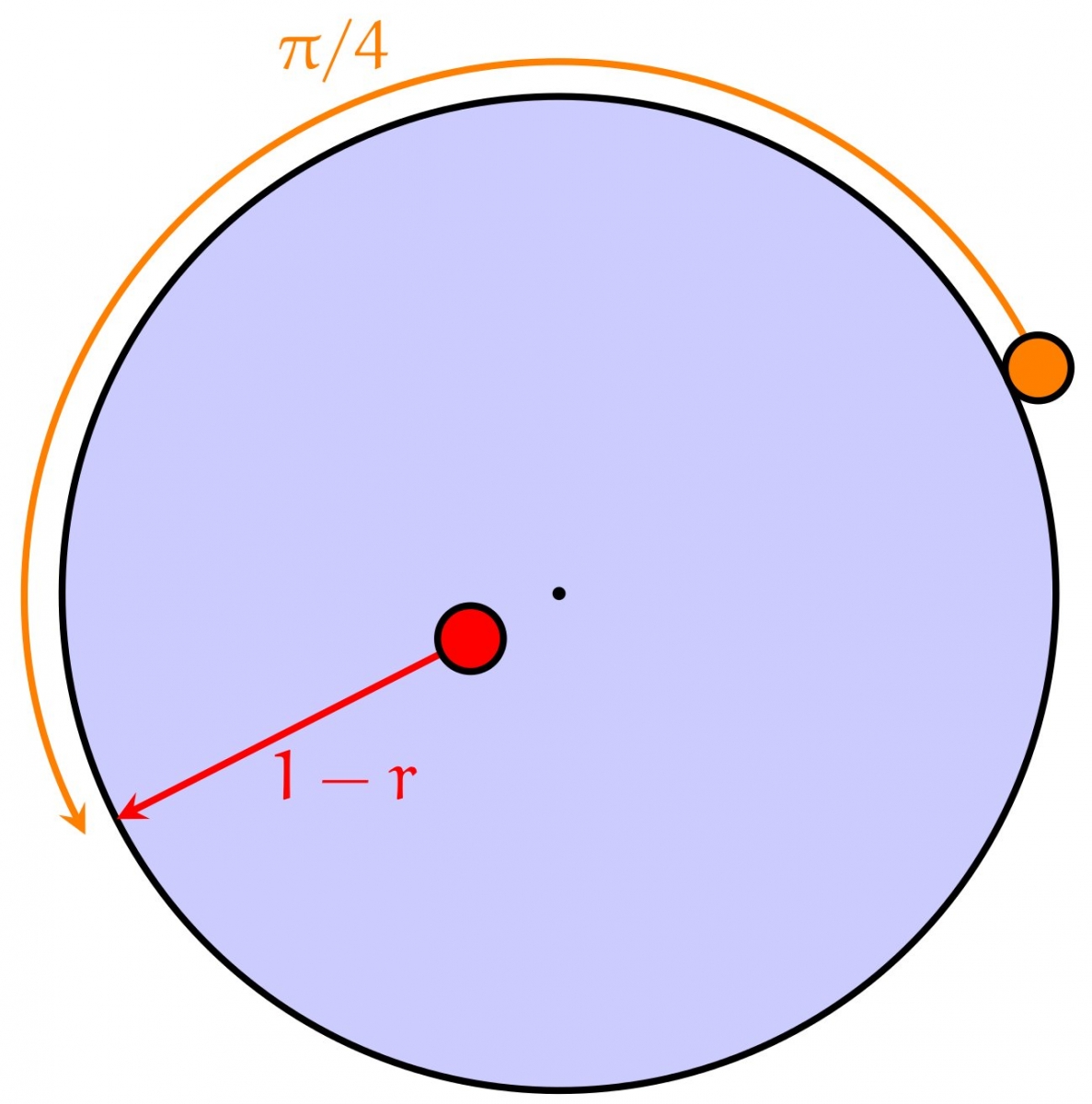
Cette fois-ci, la méthode fonctionne si (et seulement si) $1-r < \frac \pi 4$, ce qui est équivalent à $r > 1 - \frac \pi 4$.

Ainsi, notre méthode fonctionne si l'on peut trouver un rayon $r$ qui vérifie à la fois $r < \frac 14$ (pour qu'on puisse arriver à distance $1-r$ du bord en laissant le lion à l'opposée) et $r > 1 - \frac \pi 4$ (pour que la distance $1-r$ soit suffisamment courte pour battre le lion « au sprint »).

Cela est possible car \[\pi > 3 \text{ donc } 1 - \frac \pi 4 < \frac 1 4.\]

Cette question est tirée d'un sujet MATh.en.JEANS du lycée Marcelin-Berthelot de Saint-Maur. Il est assez évident que la situation proposée, qui fonctionne très bien pour un lion quatre fois plus rapide que le nageur, n'est pas optimale : des stratégies plus fines permettraient sans aucun doute d'échapper à des lions bien plus rapides (notamment allant $\lambda$ fois plus vite que la nageur, avec $\lambda \geq \pi + 1$, cas où notre stratégie échoue). Cette question semble appartenir à la thématique (difficile) des jeux différentiels. A priori, la conjecture naturelle est que la stratégie optimale pour le nageur est d'aller toujours dans la direction opposée à celle du lion (notons que cette direction change au cours du temps, alors que la phase de « sprint » dans notre stratégie se fait dans une direction constante), mais cela ne semble pas si facile à montrer...