Vous pouvez retrouver cette question au format pdf.

Question du jeudi #13 : $n + m$ boules se déplacent sur une droite. À l'instant $t=0$, les $n$ boules de gauche ont une vitesse $\vec v$ dirigée vers la droite, alors que les $m$ boules de droite ont une vitesse $- \vec v$ (dirigée vers la gauche, donc). On néglige tous les frottements et on suppose que les chocs sont élastiques, de telle sorte que la vitesse d'une boule à un instant donné est toujours $\pm \vec v$. Combien de collisions vont-elles se produire ?

La réponse est qu'il se produira $nm$ collisions. Voyons pourquoi.

Comme dans le dessin suivant, numérotons les différentes boules, afin de les identifier.

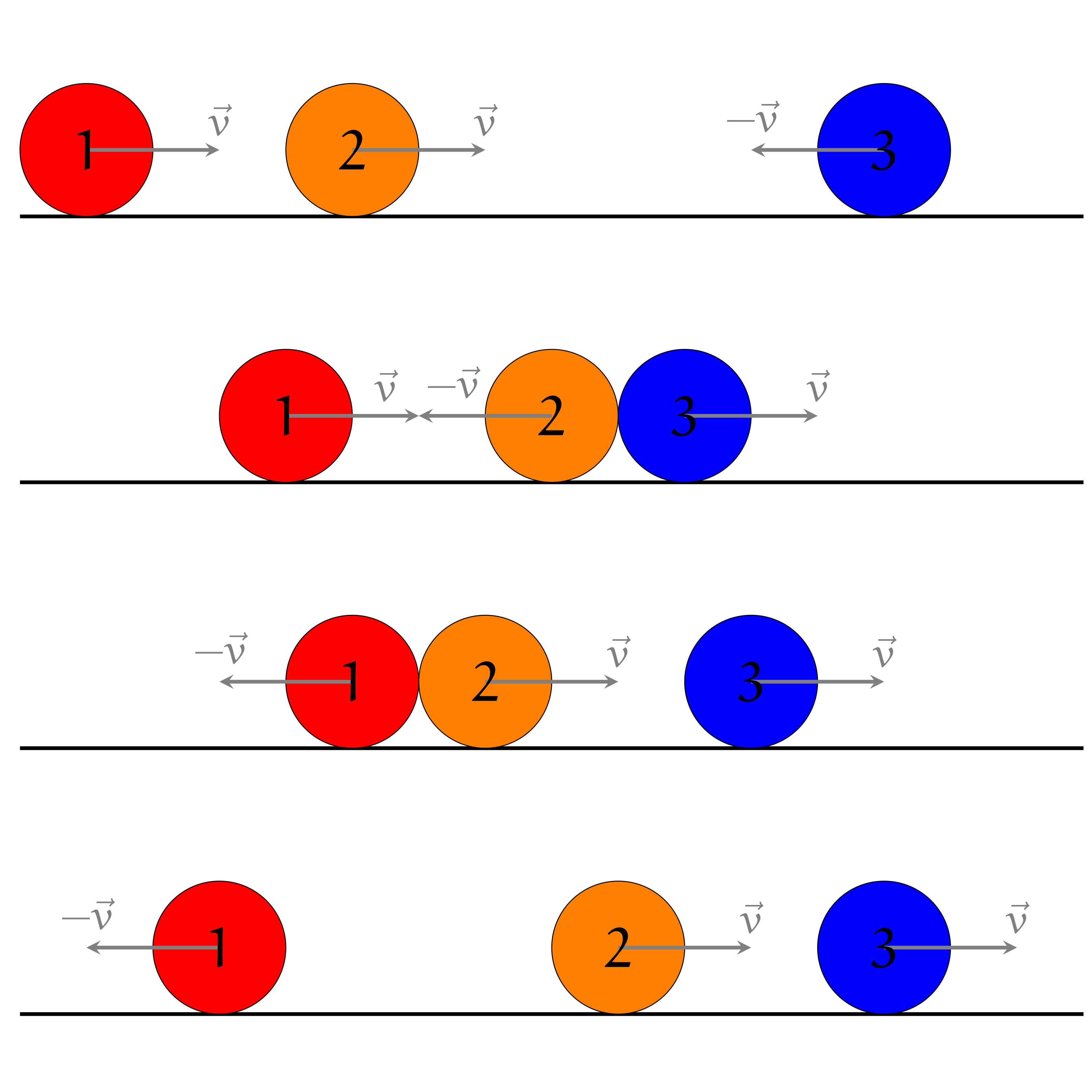
Modifions un peu l'énoncé : supposons qu'au moment de chaque choc, un événement magique survienne et que les deux boules repartent après avoir échangé leurs identités. Le dessin suivant illustre la modification.

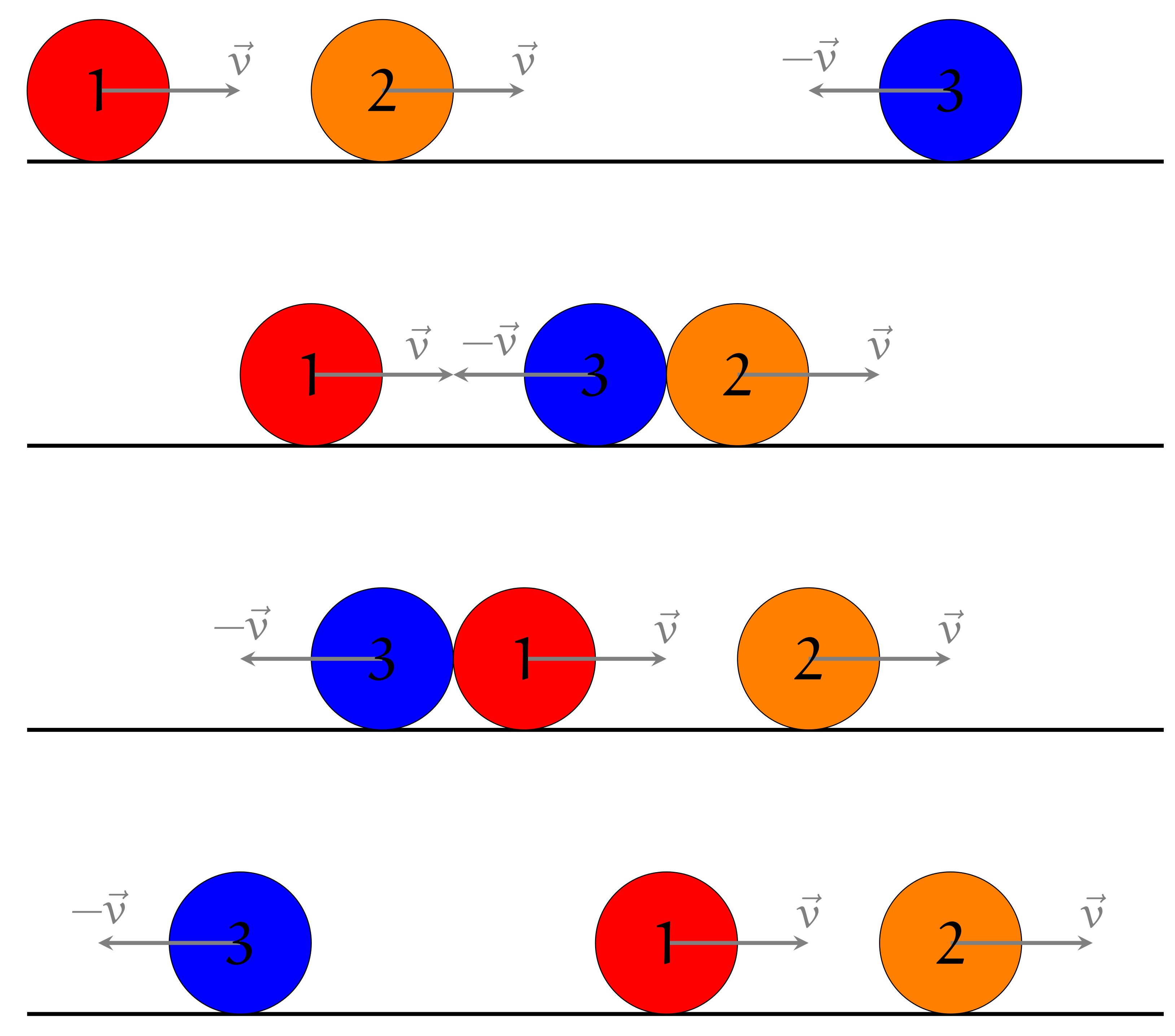
La modification ne fait que permuter les boules : à un instant donné, les $n+m$ boules sont (globalement) exactement aux mêmes endroits, et elles ont la même vitesse qu'avant la modification. En particulier, les collisions se produisent aux mêmes moments et elles sont en même nombre.

Mais la situation est maintenant plus simple à analyser : les $n$ boules initialement à gauche ont toujours la même vitesse $\vec v$ et les $m$ boules initialement à droite ont toujours la même vitesse $-\vec v$ (à part que les deux subissent une petite téléportation au moment de chaque choc, puisqu'elles échangent alors instantanément leur position avec la boule qui vient de les percuter). En particulier, chacune des $n$ boules « de gauche » va percuter exactement une fois chacune des $m$ boules « de droite. »

Il y a donc bien en tout $nm$ collisions.