Le but de cet article est de faire de la publicité pour The Aperiodical. Ce site (dont le nom est un jeu de mots mêlant journalisme et mathématiques) est un blog collectif tenu par de jeunes mathématiciens britanniques qui s'adresse, comme le dit sa présentation, à tous ceux qui savent déjà qu'ils aiment les mathématiques et qui veulent en apprendre plus. En plus de suivre l'actualité des mathématiques et de leur diffusion, ce beau site est un très bon point d'entrée dans le monde très riche de la divulgation mathématique outre-Manche et sa lecture est très agréable.
Les éditeurs de The Aperiodical ont accepté que paraisse ici une traduction d'un article de Paul Taylor intitulé How to solve a Rubik’s Cube in one easy step. Merci à eux et bonne lecture !
Comment résoudre le Rubik's Cube en un seul mouvement
Il y a quelques années, assis dans mon fauteil, je jouais avec le Rubik's cube du bureau. Je n'essayais pas de le résoudre, mais je répétais les mêmes mouvements en boucle. Plus particulièrement, je « vissais » la face de droite d'un quart de tour avant de faire tourner le cube lui-même d'un quart de tour. Comme ça :
Puisque j'avais commencé avec un cube résolu, je savais qu'en continuant à faire la même opération, le cube se résoudrait de lui-même. Mais cela ne semblait pas vouloir arriver et ça faisait déjà quelque temps que j'essayais. Cela méritait une enquête plus précise !
Une première chose à régler : comment savais-je que le cube finirait par se résoudre de lui-même si je répétais sans cesse la même opération ? Eh bien, un fait plutôt évident à propos du Rubik's cube est qu'il n'est pas aléatoire : si deux cubes sont dans le même état et que vous effectuez des deux côtés la même opération, ils finiront dans le même état. Ainsi, quand vous répétez la même opération, le cube suit un chemin bien défini, passant par certains des états dans lesquels il peut se trouver. Il y a un nombre fini de tels états possibles (à l'origine, le fabricant affirmait qu'il y en avait 3 milliards, c'est très sous-estimé, mais le nombre reste fini !) donc il finira par revenir sur ses pas. À partir de ce moment, le cube vivra une histoire sans fin : les mêmes états et les mêmes mouvements continueront à produire les mêmes résultats.
Mais cela ne prouve pas que le cube reviendra à son état initial. Pourquoi la situation décrite dans l'image suivante ne pourrait-elle pas se produire ?
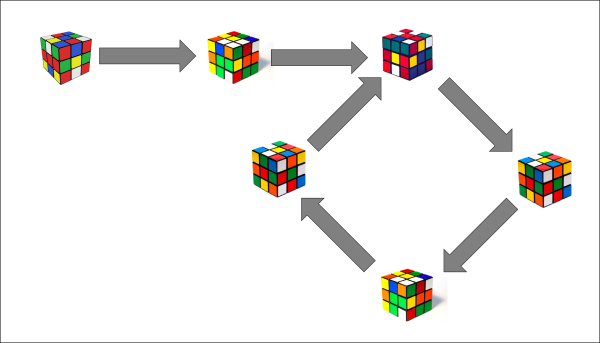
(Que ce dessin ne vous perturbe pas, il s'avèrera impossible.)
Si le cube ne revient pas à son état de départ, il doit faire ça, c'est-à-dire retourner à un état déjà parcouru (mais différent de l'état initial) et parcourir une boucle à partir de ce point. Mais regardez le premier cube de la boucle : on y arrive à partir de deux états différents. Un autre fait assez évident à propos du Rubik's cube est que tout mouvement, ou même toute suite de mouvements peut-être inversée. Si je visse une face puis que je fais tourner le cube dans ma main, je peux annuler cette opération en faisant tourner le cube dans ma main dans l'autre sens puis en dévissant la face. Faire un mouvement puis son inverse n'a aucun effet sur le cube. Supposons donc que l'on se trouve dans un des deux états juste avant la boucle et que je fasse mon opération de vissage-rotation puis mon opération rotation-dévissage. Dans les deux cas, on doit retourner à l'état dont on est parti. Mais dans les deux cas, l'opération de rotation-dévissage a amené le cube dans le premier état de la boucle. Ainsi, on est dans une situation étrange où à partir d'une position donnée (le premier état de la boucle), on obtient deux états différents en effectuant la même opération (la rotation-dévissage). On sait que ce n'est pas possible. Il n'y a qu'une seule façon de se sortir de ce paradoxe : il faut bien admettre que la boucle revient exactement à la position de départ, ce qui évite le problème des deux antécédents.
Comparez cette situation au jeu de la vie de Conway, ce jeu (sans joueur) dans lequel une grille de carrés noirs et blancs évolue au cours du temps en suivant une règle simple, et qui donne lieu à des situations d'une variété infinie. Étant donné une position du jeu de la vie, il arrive (souvent) que le jeu se bloque dans une boucle où les mêmes motifs se répètent sans repasser par l'état de départ. Cela vient du fait que le jeu de la vie n'est pas inversible : on peut très bien arriver au même état en partant de deux positions précédentes, et l'argument précédant ne s'applique pas.
On sait donc que le Rubik's cube se résoudra après un nombre fini de répétition de mon mouvement de « vissage-rotation » mais il reste une question : quand ? Comme mon bureau se trouvait à l'Université de Manchester, nous avons décidé de résoudre ce problème, et de le faire de la seule façon que nous connaissons : avec des autocollants et des ordinateurs.

(Le cube et ses autocollants, ici avec un critérium de l'Université de Manchester)
Avec les petites facettes du cube numérotées de 1 à 54, on peut suivre l'effet d'un mouvement sur le cube en regardant comment les nombres s'échangent. En vissant, on voit que la facette 1 occupera la position précédemment occupée par la facette 37, la facette 2 occupera la position précédemment occupée par la facette 38, etc. Pour faire des maths sérieuses, au lieu de répéter l'expression « occupera la position précédemment occupée par la facette », on on écrira plutôt quelque chose comme

Si l'on se sent particulièrement laconique (c'est toujours le cas), on peut noter cela de façon encore plus compacte, comme :
$$(1\ 37\ 27\ 46)(2\ 38\ 26\ 47)(3\ 39\ 25\ 48)(34\ 36\ 30\ 28)(35\ 33\ 29\ 31).$$
Ici, on part de 1, qui prend la place précédemment occupée par 37, donc on regarde ensuite 37, etc. Si on revient à la position de départ, on ferme la parenthèse, et on recommence avec le plus petit numéro que l'on n'a pas encore regardé. (Pour montrer que l'on formera ainsi des cycles bien rangés, il faut essentiellement répéter l'argument que l'on a utilisé pour montrer qu'en répétant une même opération, on finit toujours par retomber sur nos pas).
On a donc un cube plein d'autocollants, on note un numéro, on tourne ou on visse et on regarde où l'autocollant est arrivé. En faisant cela, on arrive à des cycles pour le vissage et la rotation :

Le vissage déplace quatre bandes de trois nombres et les huit facettes extérieures de la face vissée, tout cela parcourant des cycles de quatre nombres. La rotation a un effet plus radical, puisqu'elle change les positions de tous les autocollants à l'exception des deux qui se trouvent aux « pôles » de la rotation (le 5 et le 23).
Une fois que vous avez écrit les deux opérations de cette façon, il est facile de voir l'effet des deux opérations réalisées consécutivement : il suffit de suivre ce qu'il arrive à chacun des numéros. Ainsi, la première opération amène 1 à la position originale d'un autre nombre, disons $n$ (évidemment, $n$ a bougé, lui aussi). Où le deuxième mouvement amène-t-il 1 ? Eh bien, on sait où il amène $n$ quand on part du cube résolu, et l'on sait que $1$ est précisément à cet endroit, donc le deuxième mouvement amène $1$ là où il amène $n$ quand on part du cube résolu. Une fois que l'on fait cela pour chacun des nombres, on aura écrit l'opération composée vissage-rotation sous la même forme que plus haut.
À partir de là on peut déterminer le nombre de fois que l'on devra répéter l'opération pour revenir au point de départ. Cette dernière étape montre la puissance de notre notation à base de cycles. En effet, un cycle de longueur $n$ a besoin de $n$ répétitions pour que chacun des nombres qui le constitue retrouve sa position de départ. Et comme aucun des cycles n'interfère avec les autres, le nombre cherché est simplement le plus petit nombre qui est un multiple de la longueur de tous les cycles. Dès que l'on aura fait ce calcul, on saura combien de fois il faut répéter l'opération pour ramener le cube à sa position initiale. Mieux, on l'aura déterminé sans avoir eu à vraiment faire les deux mouvements l'un après l'autre (et certainement sans les répéter un grand nombre de fois). Quelle que soit la taille de ce nombre final, on aura obtenu la réponse après le même travail (modéré).
Je l'ai expliqué, il est relativement simple d'obtenir le nombre nécessaire de répétition à partir de cette information, au prix d'un calcul légèrement laborieux pour obtenir l'expression associée à l'opération de vissage-rotation, et une comparaison rapide des longueurs des cycles. Cependant, on a simplement donné les cycles à un logiciel. On a utilisé MAGMA, qui est fait pour faire des calculs dans les branches des maths dont nous sommes en train d'explorer un exemple élémentaire. Vous pouvez essayer vous-même en collant le code suivant dans le calculateur MAGMA en ligne :
G:=Sym(54); vissage:=G!((1,37,27,46)(2,38,26,47)(3,39,25,48)(34,36,30,28)(35,33,29,31)); print "Ordre du vissage"; Order(vissage); rotation:=G!((1,3,9,7)(2,6,8,4)(25,27,21,19)(20,22,26,24)(12,54,34,37) (11,51,35,40)(10,48,36,43)(13,47,33,44)(14,50,32,41)(15,53,31,38) (16,46,30,45)(17,49,29,42)(18,52,28,39)); print "Ordre de la rotation"; Order(rotation); print "Ordre de vissage*rotation"; Order(vissage*rotation);
L'ordinateur nous donne alors la réponse : $1\,260$. Si on faisait des maths sérieuses, on appellerait ça l'ordre de la suite de mouvements, ce que le nom de la commande indique. Je trouve plutôt étonnant que deux mouvements ayant individuellement besoin de quatre répétitions pour revenir à l'état de départ puissent donner un résultat si grand. Cela pose naturellement une question : quel est le plus grand nombre de répétitions dont peut avoir besoin une suite de mouvements pour revenir à la position de départ ? On peut également trouver la réponse à cette question, mais avant, un détail technique !
Un de mes mouvements était de tourner le cube d'un quart de tour. Certaines personnes pourraient dire que ce n'est pas un vrai mouvement : le cube n'a pas vraiment changé. J'aurais aussi bien pu poser le cube sur la table et me déplacer moi-même. Au lieu de dire que l'on répète l'opération vissage-rotation, les puristes parleraient d'une suite de quatre mouvements : on visse d'abord la face de devant, puis celle de droite, puis celle de derrière, puis celle de gauche. Si on répète cette suite, il nous faudra toujours $1\,260$ vissages pour revenir à la situation de départ, mais cela ne fait « que » 315 répétitions de la suite. (Détail dans le détail : si on compte une rotation du cube comme un mouvement, doit-on compter un cube résolu, mais tourné, comme revenu à sa position de départ ? J'ai l'impression qu'on le devrait, mais à partir de maintenant, il vaut probablement mieux se plier aux définitions des puristes.) Il est un peu décevant de descendre d'un impressionnant $1\,260$ à un simple 315, mais dans notre nouveau système, il est plus facile de chercher le plus grand nombre de répétitions possible.
Pour s'attaquer à une telle question, il vaut mieux mettre sur pied une notation qui permette de parler de choses comme « un vissage d'un quart de tour de la face de devant dans le sens des aiguilles d'une montre puis un vissage d'un quart de tour de la face de derrière dans le sens des aiguilles d'une montre, où *sens des aiguilles d'une monde* signifie *sens des aiguilles d'une montre quand on regarde la face concernée* ». Heureusement, la plupart des personnes qui se sont sérieusement intéressées au Rubik's cube quand il est sorti étaient des mathématiciens, donc ce n'est pas un problème. La notation standard est d'utiliser les lettres $F$, $R$, $L$, $B$, $U$ et $D$ pour représenter un vissage d'un quart de tour dans le sens des aiguilles d'une montre (du point de vue de quelqu'un qui regarderait la face) des faces de devant (front), droite (right), gauche (left), derrière (back), dessus (up) et dessous (down). Les suites de mouvements sont alors simplement indiquées comme des suites de lettres. Celle dont on parlait s'écrit donc $FRBL$. Un demi-tour de la face de droite peut s'écrire $FF$ (puisqu'il s'agit simplement de deux quarts de tour) ou, plus chic, $F^2$. Puisqu'un quart de tour dans le sens inverse des aiguilles d'une montre est simplement un quart de tour dans le sens des aiguilles d'une montre répété trois fois, on peut le noter $FFF$, $F^3$ ou $F^{-1}$ (pour l'inverse de $F$).
Les six vissages du cube correspondant à ces lettres forment un ensemble complet de mouvements de base : tout ce que l'on peut faire sur le cube peut être vu comme une suite de ces six mouvements. Ainsi, si l'on donne à un ordinateur les permutations pour ces six mouvements, et si l'ordinateur est assez intelligent, il peut nous dire quelle combinaison a le plus grand « temps de retour ». C'est plus difficile que ce que je l'ai laissé entendre : il faut déterminer la structure complète du groupe de toutes les suites de mouvements et voir comment elles se combinent. Mais si on le fait, on trouve que le nombre maximal de répétitions est un nombre familier : $1\,260$. Un tel mouvement peut s'obtenir en combinant cinq vissages (quatre quarts de tour et un demi-tour) et s'écrit $RU^2D^{-1}BD^{-1}$. Si on suppose que chaque vissage prend deux secondes, répéter cette suite jusqu'à résoudre le cube occupe trois heures et demie. Mais cette suite de mouvements est un peu complexe, et la suite de vissage-rotation sur laquelle j'étais tombé se défend déjà pas mal. En fait, 315 répétitions est le résultat optimal pour une suite d'au plus quatre mouvements : c'est une petite victoire pour la méthode consistant à passer le temps en jouant avec des objets pour déterminer leur structure mathématique profonde.
