Bernard Vitrac (CNRS - EPHE)

Pseudo-Héron, Geometrica,  Section 24, Problème 3 :

Une aire carrée ayant l'aire plus le périmètre : 896 pieds. Séparer l'aire du périmètre. Je fais ainsi :

(a) De manière universelle que soient proposées 4 unités.
(b) Dont le 1/2 produit : 2 pieds.
(c) Celles-ci, par elles-mêmes, produisent 4 pieds.
(d) Ajoute alors avec les 896; ensemble sont produits : 900 pieds.
(e) Dont le côté carré produit 30 pieds.
(f) Et à partir des 4, retranche le 1/2 : 2 pieds sont produits.
(g) Comme reste sont produits 28 pieds.

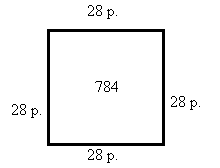
(h) Donc l'aire est 784 pieds et le périmètre est 112 pieds.
(i) Ensemble ajoute-les tous : sont produits 896; autant que ceux-là sera l'aire avec le périmètre : 896 pieds.

La formulation du problème est géométrique, mais réside dans l'application d'un algorithme, connu, dans l'algèbre élémentaire moderne, comme la méthode dite de « complétion du carré ».
Commentaire algébrique : On note c le côté du carré. Son aire est S = c², son périmètre p = 4c.
Le problème posé peut donc se transcrire : c² + 4c = 896, cas particulier de l'équation du second degré :

x² + ax = b. Pour trouver S et p, il faut calculer c. On peut remarquer que c'est fait à l'étape (g : c = 28), mais ce n'est pas dit. Seuls S et p sont spécifiés à l'étape (h).
Pour trouver c, l'inventeur du problème suit une procédure que l'on peut transcrire de la manière suivante :

On prend la moitié de a que l'on multiplie par lui-même :

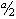
(étapes a-b-c).

On ajoute b et on calcule

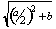
(étapes d-e)

Et on retranche

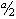
La solution est c =

-

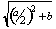
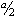
(étapes f-g)

Ici on trouve 28; on calcule S = (28)² = 784 et p = 4 . 28 = 112 (h). On vérifie que leur somme fait bien 896 (i).