Ptolémée construit ses tables de cordes à l'aide des quatre règles démontrées ci-dessous.
Règle 1: corde sous-tendue par l'angle supplémentaire
|
CA² + AB² = BC². Comme BC = 120, BC² = 14400.
Si on connait AB on peut donc calculer AC.
|
Règle 2: corde sous-tendue par l'angle moitié
|
On place CE égale à CA, on joint DE et on mène la perpendiculaire DF. Dans le triangle BCD, rectangle en D, la droite DB est moyenne géométrique des droites BC et BF (Euclide, VI. 8);
donc DB2 = BC.BF. Or BC vaut 120.
Règle 2 : cord (α/2) = √(60.[120 - cord (180°- α)]) |
Règles 3 et 4 : corde sous-tendue par la différence et la somme de deux angles
|
Soit E le point sur AC tel que l'angle ABE soit égal à l'angle DBC. On vérifie que les triangles ABD, BCE sont équiangles donc semblables.
D'où : BC : CE :: BD : AD, soit : AD.BC = CE.BD (*). En additionnant (*) et (**) : AD.BC + AB.CD = CE.BD + AE.BD = (AE + EC).BD = AC.BD. A partir de là, si on se donne deux cordes AB, BC, on peut calculer les cordes sous-tendues par la différence ou la somme des arcs.
Par la règle n°1 nous pouvons calculer BD et CE. D'après le théorème de Ptolémée appliqué à BCDE, on a : BD.CE = BC.DE + BE.CD.Dans cette égalité BD, CE, BC, DE, BE sont connues. On en déduit CD. De nouveau, par la règle n°1, on obtient AC.Règle 3 : 120 cord (α - β) = cord (α). cord (180° - β) - cord (β). cord (180° - α) Règle 4 : 120 cord [180° - (α + β)] = cord (180° - α).cord (180° - β) - cord (α).cord (β) |
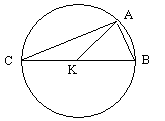 Soit AB une corde sous-tendue par l'angle AKB et AC la corde sous-tendue par l'angle supplémentaire. BC est donc un diamètre donc le triangle ABC est rectangle en A et, d'après le théorème de l'hypoténuse (Euclide, I. 47), on a :
Soit AB une corde sous-tendue par l'angle AKB et AC la corde sous-tendue par l'angle supplémentaire. BC est donc un diamètre donc le triangle ABC est rectangle en A et, d'après le théorème de l'hypoténuse (Euclide, I. 47), on a :
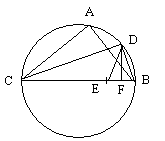 Soit AB une corde et AC la corde sous-tendue par l'angle supplémentaire. On coupe l'arc AB en deux parties égales au point D. On veut calculer la corde BD, corde de l'angle moitié.
Soit AB une corde et AC la corde sous-tendue par l'angle supplémentaire. On coupe l'arc AB en deux parties égales au point D. On veut calculer la corde BD, corde de l'angle moitié.
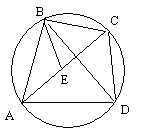 Soit ABCD un quadrilatère quelconque inscriptible dans un cercle. Alors le produit des diagonales (Ptolémée dit le rectangle contenu par AC, BD) est égal à la somme des produits des côtés opposés (les deux rectangles contenus par (AB, CD) et (AD, BC) respectivement.
Soit ABCD un quadrilatère quelconque inscriptible dans un cercle. Alors le produit des diagonales (Ptolémée dit le rectangle contenu par AC, BD) est égal à la somme des produits des côtés opposés (les deux rectangles contenus par (AB, CD) et (AD, BC) respectivement.
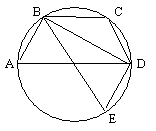 Cherchons, par exemple, AC. On mène les diamètres AD et BE. On a donc AB = DE et DE est connue.
Cherchons, par exemple, AC. On mène les diamètres AD et BE. On a donc AB = DE et DE est connue.