Essayons de voir ce qui se passe pour un nombre restreint de récipients.

• Pour un seul récipient, aucun problème : le récipient contient alors un litre, donc en partant de l'endroit où il se trouve, on a de quoi faire le tour du circuit.
• S'il y a deux récipients, c'est un peu plus compliqué. Partir du récipient le plus rempli ne marche pas forcément : si le premier récipient contient 2/3 de litre, mais qu'il faut faire 3/4 de tour avant d'arriver au second, alors on tombera forcément en panne sèche.En fait, il faut alors partir de celui des deux récipients dont la quantité d'essence permet d'atteindre l'autre. L'un des deux au moins remplit forcément cette condition, car si l'on note q(X) la quantité d'essence d'un réservoir X donné et d(X) la distance (exprimée en fraction de tour de circuit) jusqu'au réservoir suivant, la condition demandée est qu'il existe un réservoir X tel que q(X) soit supérieur ou égal à d(X). Et, si l'on appelle A et B nos deux réservoirs, on a q(A) + q(B) = 1 et d(A) + d(B) = 1 (*), on ne peut donc avoir q(A) < d(A) et simultannément q(B) < d(B). Une fois arrivé au second réservoir, aucun problème : on a alors récupéré toute l'essence, donc on est en mesure de terminer le tour.

• Pour trois récipients, c'est un peu plus compliqué : si l'on appelle A, B et C nos trois réservoirs, il ne suffit pas de trouver un réservoir X tel que q(X) soit supérieur ou égal à d(X). Cette condition suffit en effet à atteindre le deuxième réservoir, mais il se peut alors que l'on tombe en panne sèche entre le deuxième et le troisième.
  En réalité, il suffit d'avoir q(X) supérieur ou égal à d(X) et q(X) + q(Y) supérieur ou égal à d(X) + d(Y), où Y est le réservoir suivant. Mais comme on a toujours la contrainte q(A) + q(B) + q(C) = 1 et d(A) + d(B) + d(C) = 1 (**), la deuxième partie de cette condition revient à dire que q(Z) est inférieur ou égal à d(Z), où Z est le troisième réservoir !
  Trouver un point de départ qui convient est alors on ne peut plus simple. Par (**), on sait que l'un des trois réservoirs au moins vérifie la condition "q(X) est inférieur ou égal à d(X)". Quitte à changer les noms des réservoirs, on peut supposer que le réservoir A vérifie cette propriété.
  On compare alors q(B) et d(B). Si q(B) est supérieur ou égal à d(B), alors B convient comme point de départ. Sinon, toujours grâce à (**), q(C) est forcément supérieur à d(C), et alors C convient comme point de départ.

On pourrait continuer avec quatre récipients, etc. Mais visiblement, la situation se complique à chaque fois un peu plus. Nous allons maintenant présenter deux solutions au problème. La première est inspirée par les considérations précédentes : il s'agit de démontrer l'existence d'une position de départ adéquate par récurrence sur le nombre de récipients.

•  Le résultat est vrai lorsqu'il n'y a qu'un récipient, comme nous l'avons déjà vu.
•  Supposons donc le résultat vrai pour n récipients, et soit une situation dans laquelle le litre d'essence est divisé en n+1 réserves.Nous allons voir que l'on peut se ramener à une situation avec seulement n récipients. Par le même raisonnement que précédemment (cas n=2 ou 3), il existe un réservoir X tel que q(X) soit supérieur ou égal à d(X). Nous allons voir que le problème est le même si l'on ajoute à un tel réservoir, à l'endroit où il est, le contenu du réservoir suivant.En effet, soit A un tel réservoir et B le réservoir suivant. Si l'on arrive au point A, on arrive nécessairement jusqu'à B puisqu'il y a en A une quantité d'essence suffisante pour ce faire. Et, en arrivant en B, on a dépensé la quantité d'essence d(A) depuis le point A. Si q désigne la quantité d'essence dont on dispose en arrivant en A, on a en B la quantité

    q + q(A) - d(A)

    quantité à laquelle on doit ajouter la quantité q(B) que l'on récupère en B. C'est-à-dire que l'on a en repartant de B la quantité

    q + q(A) - d(A) + q(B)

    On trouve la même chose s'il y a une quantité q(A) + q(B) au point A, et rien au point B. Comme de toutes façon il est impossible de partir d'un point strictement compris entre A et B (on partirait sinon avec le réservoir vide !), on peut regrouper nos deux réservoirs au point A et ça ne change pas le problème.

    Comme par hypothèse de récurrence il y a une position de départ qui convient pour n récipients, il y en a aussi une pour notre situation à n+1 récipients.

•     On conclue par récurrence qu'il existe toujours une position de départ qui convient.

Une autre démonstration existe, bien plus efficace : il s'agit d'un argument graphique. Considérons une position de départ arbitraire sur le circuit, et traçons la courbe représentative de la quantité algébrique d'essence reçue en fonction de la distance parcourue (on suppose que la voiture dispose au départ de suffisemment d'essence pour faire le tour quoi qu'il arrive, mais qu'elle va quand même récupérer l'essence disponible).

• Entre deux réservoirs, la voiture ne reçoit pas d'essence, mais en dépense, à un rythme constant (une unité d'essence par unité de distance). D'où une courbe représentative qui est alors une droite de pente -1.
• À chaque réservoir, en revanche, la voiture reçoit instantannément une quantité d'essence. Ceci se traduit par un saut de la courbe. Comme la quantité totale d'essence disponible est 1 litre, la somme des sauts est de 1.
• Et comme la voiture a dépensé en tout 1 litre également, la courbe a au total baissé de 1 et monté de 1, c'est-à-dire que l'on revient au niveau de départ.

Exemple :

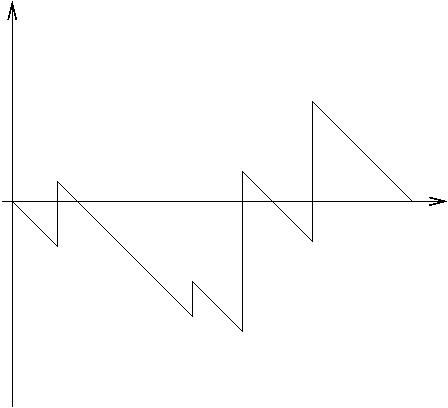
Si l'on continuait de la sorte (la voiture ravitaillant à chaque tour de la même façon, c'est-à-dire de la même quantité aux mêmes endroits), on obtiendrait une fonction périodique, de période 1.
Pour trouver une position de départ qui convient, il suffit de se placer au point où notre courbe atteint son minimum : si l'on trace la même courbe que précédemment, c'est-à-dire celle de la quantité algébrique d'essence reçue en fonction de la distance parcourue à partir de ce point, on obtient la courbe :

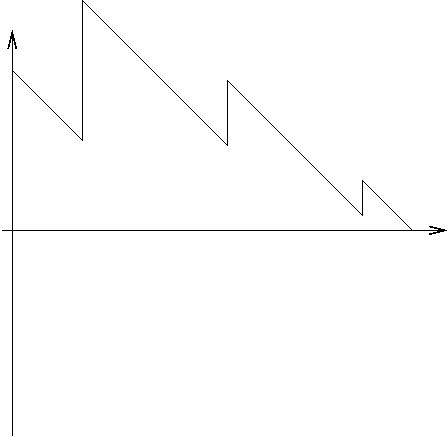
Cette courbe est toujours au-dessus de l'axe des abscisses, ce qui signifie que le réservoir ne s'assèche pas (ou éventuellement à l'endroit exact d'un ravitaillement). Autrement dit, la voiture pourra faire le tour complet du circuit en partant de ce point !