Curieusement, une façon assez simple de s'en sortir est de voir ce problème comme un problème de calcul propositionnel. On utilisera les notations traditionnelles de calcul propositionnel :

	désigne le connecteur "ET"
	désigne le connecteur "OU"

Considérons cinq variables propositionnelles A, B, C, D et E. À chaque situation possible (présence d'un certain nombre de gens parmis Alice, Bernard, Christine, Dominique et Émile), on associe une distribution de valeurs de vérités sur notre ensemble de variables, de la façon suivante :

• si Alice est présente, alors A est vraie (i.e. la variable A vaut 1), sinon elle est fausse (elle vaut 0).
• si Bernard est présent, alors B est vraie, sinon B est fausse.
• idem pour Christine, Dominique et Émile.

La formule d'ouverture du coffre s'écrit alors aisément en fonction de nos variables propositionnelles : le coffre s'ouvre si et seulement si

Alice ET Bernard sont là, c'est-à-dire		vaut 1.
Ou alors Alice, Christine ET Dominique sont là, i.e.		vaut 1.
Ou enfin Bernard, Dominique ET Emile sont là, i.e.		vaut 1.

Autrement dit, la formule d'ouverture du coffre s'écrit :

En utilisant les règles de distibutivité de la disjonction par rapport à la conjonction et réciproquement, on peut alors transformer cette écriture, pour passer d'une disjonction de conjonctions au contraire (conjonctions de disjonctions). Cette transformation formelle semble anodine, mais nous allons voir qu'elle permet de répondre directement à notre problème. Transformons donc. Pour faciliter la lecture, nous allons d'abord transformer une partie seulement de l'expression :

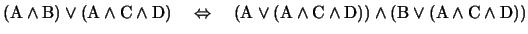
Rappelons ici tout de suite les lois d'absorption :

	(1)
	(2)

En effet, si P est vraie, alors

est vraie, et réciproquement. Idem pour

Appliquant (1) à P = A et

, on obtient :

Pour la dernière équivalence, on a appliqué (2) à P = A et Q = B.

Passons maintenant à la totalité de la formule d'ouverture du coffre à savoir, en appliquant l'équivalence précédente :

On trouve mécaniquement, en distribuant le terme

Là encore, nous allons transformer les termes un par un :

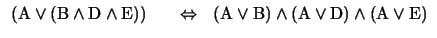
Pour les deux autres termes on constate avec joie que les lois d'absorption s'appliquent. En posant

P = B et

on trouve

De même

On obtient donc comme expression pour la formule du coffre :

OUF ! Il ne reste plus qu'à interpréter cette formule en termes de coffre fort. Ceci signifie qu'il sera ouvert lorsque seront réunis :

• Alice ou Bernard, à qui l'on donne donc une clé (chacun) de la première serrure.
• Alice ou Dominique, à qui l'on donne une clé de la deuxième serrure.
• Alice ou Emile, à qui l'on donne une clé de la troisième serrure.
• Bernard ou Christine, à qui l'on donne une clé de la quatrième serrure.
• Bernard ou Dominique, à qui l'on donne une clé de la cinquième serrure.

C'est-à-dire cinq serrure suffisent à répondre au problème. Comme de plus aucune des conditions précédentes n'est conséquence des autres (par exemple, si seuls Alice et Christine sont présentes, les quatre premières conditions sont réunies, mais pas la cinquième), il faut donc au moins cinq serrures.

Il faut cinq serrures.