Frédéric Brechenmacher, Centre Alexandre Koyré

 

 

Le théorème suivant est énoncé par Jordan dans son Traité des Substitutions de 1870.

 

THEOREME. - Soit

A = |x, x',...ax+bx'+..., a'x+b'x'+ ..., ... |

une substitution linéaire quelconque à coefficients entiers entre n indices variables chacun de 0 à p-1; Soient F, F', ... les facteurs irréductibles de la congruence de degré n

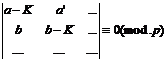
l, l', ... leurs degrés respectifs ; m, m', ...  leurs degrés de multiplicité ;

On pourra remplacer les n indices indépendants x, x', ...  par d?autres indices jouissant des propriétés suivantes :

1° Ces indices se partagent en systèmes correspondants aux divers facteurs F, F',... et contenant respectivement lm, l?m?,? indices ;

2° Soient K₀, K₁, ..., K_t-1 les racines de la congruence irréductible F≡0 (mod.p) ; les n indices du système correspondant à F se partagent en l séries correspondantes aux racines K₀, K₁, ..., K_l-1 ;

3° Les indices de la première série de ce système sont des fonctions linéaires des indices primitifs, dont les coefficients sont des entiers complexes formés avec l?imaginaire K₀ ; ils constituent une ou plusieurs suite y₀, z₀, u₀,..., y'₀, z_'0,...;...(*) telles que A  remplace les indices y₀, z₀, u₀, ... d'une même suite respectivement par K₀y₀, K₀(z₀+y₀), K₀(u₀+z₀), ...;

4° Les indices de la r+1^ième série sont les fonctions y_r, z_r, u_r,...; y'_r, z_^'r,...;... respectivement conjuguées des précédente, que l?on forme en y remplaçant K₀ par K_r ; A les remplace respectivement par

K_ry_r, K_r(z_r+y_r), K_r(u_r+z_r,...;...)

 

Cette forme simple

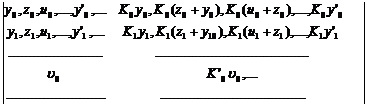
à laquelle on peut ramener la substitution A par un choix d?indice convenable, sera pour nous sa forme canonique.

[Jordan, 1870, 127].