Alain Le Mignot
 

---

SOMMAIRE

1.Comment la logique a-t-elle évoluée après Boole ?

2. Retour du côté des philosophes anglais

3. Après la mort de Boole

4. Une variante "spontanée"

5. Venn et Carroll successeurs de Boole

6. Extensions

7. Du côté de l'Allemagne

8. Un mathématicien allemand

9. Un autre

10. Quel bilan?

Encart: Les textes originaux des citations

Bibliographie

1- Comment la logique a-t-elle évoluée après Boole ?

Nous avons vu dans le chapitre précédent comment et dans quelles conditions le travail de Boole a fait exister un calcul logique efficace. La conséquence immédiate en est un déplacement de la position de la logique dans l'agencement des connaissances : après plus de vingt siècles d'ancrage dans le domaine philosophique, c'est dès lors vers les mathématiques que se retrouve positionnée l'antique création d'Aristote. Il s'agit là d'une rupture considérable pour les contemporains de Boole et il nous est peut être difficile d'en prendre toute la mesure puisque cette situation nous est familière. Il reste alors à voir par quels processus et quelles médiations l'avancée de Boole s'est trouvée confortée de sorte qu'à la fin du dix-neuvième siècle le basculement vers les mathématiques, tel que nous le connaissons, était achevé.

Il est facile de concevoir que les logiciens, quasiment tous de formation philosophique à l'époque, aient pu être déconcertés, voire choqués par les calculs de Boole, et ceci d'autant plus que rares étaient ceux possédant en même temps une formation mathématique. Ils n'étaient pas préparés à accepter la mutation de leur discipline et la réaction de rejet fut parfois vive.

Le cœur du processus calculatoire de Boole met en évidence une espèce de calcul automatique, agissant en aveugle. Ceci est la manifestation d'une séparation réelle et assumée entre le registre des opérations qui permettent le calcul et le registre de la signification qui intervient d'une manière distincte. On peut alors estimer qu'à ce moment la logique perd le contrôle de la pensée, ce qui peut déconcerter si l'on considère que son rôle est justement de guider d'une manière juste chaque étape des raisonnements. Cette question complexe produira de nombreux débats, prises de position, tentatives de médiation, avancées, adaptations mais aussi des crispations.

La réception du travail de Boole, compte tenu des ruptures fondamentales qu'il met en évidence, sera loin d'être automatique, mais sera fonction du positionnement de chacun quant aux relations mutuelles entre philosophie, logique, algèbre et géométrie, et ces relations vont rapidement évoluer.

Si dans un premier temps, la logique reste affaire de philosophes, assez vite le terrain sera investit durablement par des mathématiciens dont les préoccupations rejoignent les problèmes logiques, avec une forte composante allemande qui s'exprimera dans deux directions principales. Parallèlement, la création des états modernes permettra la structuration d'une véritable communauté mathématique internationale à travers des institutions et un réseau de revues spécialisées. Les personnalités qui émergent alors, et dont nous mettrons en avant les efforts pour développer la logique, ne doivent pas faire oublier qu'elles ne manifestent que la partie la plus saillante de travaux variés. A la fin du siècle, non seulement la logique aura basculé du côté des mathématiques, mais encore elle servira d'outils à leur réorganisation. Vers 1900, l'onde de choc booléenne est absorbée au niveau mondial et une ère nouvelle peut commencer.

Au XIX° siècle, les mathématiques sont un lieu de tensions importantes qui vont interférer avec la manière dont la nouvelle logique doit trouver sa place. Le grand problème qui est posé, sans toutefois être toujours clairement perçu, est celui de la séparation de l'algèbre et de l'analyse. Nous en avons vu ses manifestations dans la formation de la pensée de Boole puisque les algébristes anglais refusaient cette séparation. Par exemple D. Gregory dans divers travaux de 1839 utilise l'Algèbre Symbolique de Peacock pour tenter d'unifier le calcul différentiel et le calcul des différences finies en faisant porter les calculs directement sur les écritures Δ et d /dx, indépendamment de leur application à des fonctions, travaux qui sont connus de Boole.

Ce qui est en cause, et débouchera sur la « crise des fondements » à la fin du siècle, n’est rien d’autre que la légitimation de la notion de limite qui se manifeste à travers l’intégration des fonctions et la convergence des séries. Ces problèmes, contenus en germe dans les travaux de Joseph Fourier (1768-1830), donneront naissance à une multitude de questions connexes dont la maitrise se fera, très progressivement, par la création de la théorie des ensembles et de la topologie (et on trouve là l’intérêt de disposer d’un calcul sur les classes) d’une part, mais aussi par l'approfondissement de la notion de fonction et l’interrogation de la nature des nombres et donc de la manière dont ils interfèrent.. Hermann Grassmann (1808-1877) pose la question des algèbres dans Die lineale Ausdehnugslehre dès 1844, puis en 1862 dans une version remaniée (car la première mouture n’a pas eu grande répercussion) et son frère Robert (1815-1901) repose le problème en 1872 dans un ouvrage peu diffusé Die Formenlehre oder Mathematik. La résolution du problème des nombres «  imaginaires » par l’interprétation géométrique au début du siècle a montré qu’il pouvait exister un autre type de calcul ne portant pas directement sur des objets numériques, posant alors clairement le problème de l’existence d’algèbres au pluriel. L’algèbre de la logique trouve un écho dans ce questionnement car elle est un prototype de ce qui est possible, bien qu’encore non réalisé. Mais en même temps ce questionnement interrogeait de manière nouvelle le rôle de la géométrie. En 1849, De Morgan ne manquera pas de traiter, d'une manière très nouvelle pour l'époque (mais sous la forme que nous connaissons bien de couples module-argument) la trigonométrie dans Trigonometry and double algebra. Ce rapprochement avec la géométrie montre la possibilité de plusieurs algèbres. La découverte de August Möbius (1790-1868) : Der barycentrische Calcül dès 1827, d'un calcul non numérique, ainsi que celle des quaternions par W. R. Hamilton (1805-1865) en 1843, suivie des multiples travaux qui s’en inspirèrent en sont une des manifestations.

2- Retour du côté des philosophes anglais

Dans un souci de clarté il faut revenir d'abord sur l'environnement philosophique de Boole car il conditionne la manière dont Les Lois de le Pensée sera reçu et permet de comprendre certaines réactions.

Boole souligne lui-même dans certains passages de Mathematical analysis of logic et Laws of though l'existence d'un positionnement philosophique en référence aux discussions en cours. Il est utile de préciser ce point pour mieux comprendre à la fois les motivations de sa démarche et certains obstacles dans la réception de son travail.

Notons d'abord une instructive (et amusante ?) prise de position, antérieure aux publications de Boole, due au philosophe écossais Hamilton que nous avons déjà rencontré polémiquant avec De Morgan au sujet de la quantification du prédicat. Une partie annexe de l'ouvrage "Discussion on philosophy and litterature, education and unversity reform" de 1853, qui est une réunion de certains de ses articles publiés antérieurement, traite de la logique. Il y discute en particulier des travaux de De Morgan et des positions de la "Philosophical Society" de Cambridge, et manifeste à cette occasion un rejet des mathématiques à la limite de la caricature :

On ne pas dire que le contexte soit spontanément favorable à la tentative de Boole !

Mais c'est surtout des conceptions de John Stuart Mill (1806-1873) que Boole se démarquera. Mill a exercé une influence considérable sur la philosophie anglaise à travers son volumineux ouvrage de 1843, A System of Logic Ratiocinative and Inductive. Globalement, pour cet empiriste, représentant de l'école utilitariste, très loin de toute pensée symbolique, celles des connaissances qui ne sont pas intuitives nous viennent, à travers les sens, du processus logique d’induction et c’est lui qui constitue le moyen fondamental d'élaboration de la science. Par exemple, l'observation persistante du genre humain nous a montré que tout homme finit par mourir au bout d'un certain temps et ainsi l'induction nous permet affirmer que "Tout homme est mortel". C’est donc l'étude de ce processus d'induction qui est primordial et l’aspect déductif apparaît alors comme secondaire. Ce dernier n’occupe, à ce titre, qu’une partie modeste de la logique qui, ainsi comprise par Mill, est à la base de toute science, l'algèbre se trouvant réduite à un simple système de notations. Pour Mill :

C’est en vain que l’on chercherait, dans cet ouvrage de Mill de plus de mille pages, la moindre formule qui pourrait faire penser à une idée formelle de calcul; tout est rhétorique puisqu’il s’agit de philosophie.
Boole récuse fortement les conceptions de Mill concernant la logique :

Et de même sur les fondements de la connaissance : si nous arrivons à connaître la nature, c'est parce qu'elle est subordonnée à un principe d'ordre que nous pouvons percevoir à travers l'expérience :

Cet Ordre se manifeste, à travers le langage, dans les lois de la pensée, et le traitement par l'algèbre symbolique ne fait qu'en rendre compte.

Remarquons au passage que tous les auteurs cités se réfèrent spontanément aux opérations de l'esprit en utilisant le vocabulaire des combinaisons. Bien qu'ils aient des interprétations souvent très différentes, ils partagent un bagage commun hérité de Locke.

On voit donc que Boole s'est positionné sans ambigüité dans le débat d’idées commencé avant ses publications, mais aussi que la logique était traversée, elle aussi à cette époque, par la réorganisation nécessaire des connaissances. Le travail de Boole, en faisant basculer pour la première fois la logique du côté des mathématiques, n’a fait qu’amplifier l’âpreté des arguments de cette tension qui va durer et le débat se poursuivra au moins jusqu’à la fin du siècle.

3- Après la mort de Boole

Après la publication de L’analyse mathématique de la Logique et des Lois de la Pensée, une des premières réactions vient de William Stanley Jevons (1835–1882) ), qui a été élève de De Morgan à l'université de Londres. Ainsi, s'il n'est pas lui même mathématicien, il possède une culture mathématique, ce qui ne semble pas habituel pour les logiciens de l'époque.

En écrivant Pure Logic or the science of quality apart of quantity en 1863, Jevons, qui sera reconnu plus tard surtout comme économiste, revendique une vision purement intensive, comme le souligne à dessein le titre complet de son livre. Sur cette base, il vise à débarrasser la logique de l'usage de l'algèbre qui est pour lui liée à la quantité. Il explique :

Sa position est finalement assez proche de celle de Hamilton lorsqu'il plaide pour une séparation entre la logique et les mathématiques pour des raisons liées à leur nature, formulant sans ambigüité quatre objections à l’encontre de Boole :

Précisons que Boole n'a jamais dit que la logique était une partie des mathématiques ; c'est son utilisation des notations mathématiques qui induit cette impression. Pour Boole, les mathématiques et la logique relèvent simplement d’un même calcul symbolique. Jevons assimile mathématiques et science de la quantité et surtout n'arrive pas à accepter la séparation entre le calcul et la signification, qui est caractéristique de l'Algèbre Symbolique. C'est sur cette base qu'il rejette le système de Boole. Son expression d'"habillage mathématique" pour le qualifier est un contre-sens par rapport aux motivations de Boole. Ces incompréhensions, venant d'un lettré de formation mathématique, nous donnent une idée du caractère choquant et difficile que pouvait revêtir l'application tout à fait nouvelle de l'algèbre à la logique pour les contemporains de culture philosophique, et des réactions de rejet qu'elle pouvait produire.

Mais d'un autre côté, la "greffe mathématique" est en train de prendre puisque Jevons utilise, sans discussion, l'avancée booléenne de notation des objets logiques (qui pour lui sont des noms décrivant les qualités d'une chose) par une symbolique de type algébrique, et parle même d'algèbre des qualités.

La combinaison des termes (la conjonction) est notée chez lui par juxtaposition multiplicative des symboles. L'addition n'est pas définie comme opération mais traduit une écriture des "plural terms" (ceux des termes qui ont plusieurs significations) et est, très naturellement, inclusive. Il peut alors reconnaître parmi les lois fondamentales du calcul logique, la "law of unity": A + A = A, mais n’en tire aucune conséquence particulière.

D’autre part sa notation des "contrary terms" par un changement de casse dans l’écriture (un basculement d'écriture des lettres majuscule-minuscule à la manière de De Morgan), ne permet pas un traitement fonctionnel de son système. En effet, comme il ne considère pas la négation comme une transformation, mais seulement comme une notation, ce système n'est pas apte à résoudre des équations. Bien sûr il ne risque pas de trouver les 'monstres' qu'il dénonce puisque son système n'utilise pas de division et ne résout pas d'équations. Il lui faut trouver un substitut au « development » que nous avons vu jouer un rôle central chez Boole lors de la résolution des équations.

Jevons expose sa méthode d’ « indirect inferences » en la comparant à la réduction à l’absurde d’Euclide. Elle consiste, en partant d’une équation, à multiplier les deux membres successivement par tous les produits formés à l’aide des inconnues ou de leur négation. Ainsi on est conduit à mettre en évidence des combinaisons nécessairement nulles qui permettent de traiter le problème posé. Cette idée revient à décomposer l’univers du discours en fonction des termes (les variables) du problème et de leur négation. Il souligne :

Figure 1 Les lois de Jevons et un exemple d'application [Jevons, 1864, p. 41 et 66]

Soulignons ici la référence à Euclide, qui fait un retour dans la seconde moitié du XIX° siècle. C'est encore une manière de se démarquer de Boole qui procède, non pas par axiomes et déductions, mais par analogie avec l’algèbre à travers son principe de transfert.

Par rapport aux calculs de Boole, qui s'appliquaient aussi aux probabilités, le système exposé par Jevons n'est pas vraiment un progrès. Par ses limitations intrinsèques, dues aux options de son auteur, il ne donne lieu qu'à des calculs élémentaires et ne permet pas une éventuelle extension ou un développement vers d’autres domaines. Par contre, une écriture "algébrique" de la logique semble rentrer dans les mœurs.

Après la mort de Boole, on trouva dans ses papiers un texte non daté dans lequel il regrettait, concernant "Les lois de la pensée", de s'être placé dans un cadre trop mathématique, et un autre où il envisageait de reprendre toute la présentation sous la forme d'un système philosophique, ce qu'en fait il ne fit jamais. On peut y voir un effet puissant des réactions d'incompréhension face à son travail. Sa veuve, Mary Everest Boole, et son ami De Morgan décidèrent de ne pas publier ces « remords » pour ne pas accentuer le phénomène de rejet et nuire à l'image du savant. C'est seulement en 1952 que ces textes furent rendus publics dans "Studies in Logic and Probability by George Boole" édité par R. Rhees, Watts & Co. Londres. Ceci n'est qu'une illustration supplémentaire de la difficulté qu'eut le système de Boole à s'imposer.

4- Une variante "spontanée"

Hugh MacColl (1837-1909), qui gagne chichement sa vie en enseignant les mathématiques dans un collège municipal à Boulogne sur Mer, pose le problème de changer l’ordre d’intégration pour les variables dans une intégrale quadruple. Et à cet effet il fabrique directement, avec des notations personnelles très ramassées, un calcul propositionnel, sans passer par un calcul des classes, dans une publication à Londres en 1877 : The calculus of equivalent statements and integration limits qui sera suivie de six autres. Il ne connait alors Boole qu’à travers ce qu’en rapporte Alexander Bain (1818-1903) dans sa Logic de 1870. Bain est un disciple de Mill, et sa Logic en deux parties : I Déduction, II Induction. fit connaître (paradoxalement) les nouvelles idées en logique car le volume I inclut un chapitre intitulé "Recent additions to the syllogism" dans lequel il présente les résultats des travaux de De Morgan, Hamilton et Boole. Après avoir lu Boole et Jevons, MacColl soulignera sa propre originalité dans son troisième article en 1878 :

En effet, les objets qui sont traités sont les propositions de toute nature, et les outils de base qui permettent de construire toutes les règles des calculs dont elles relèvent sont l’implication et la négation, qui est considérée fonctionnellement (comme le souligne l'auteur). Il n'est plus question d'Algèbre de la Logique, mais d'un calcul propositionnel complet tel que nous le connaissons qui est ici élaboré pour la première fois. Le but fixé de changer l’ordre des variables d'intégration est dépassé très largement. C'est un problème de pure technique mathématique qui débouche directement sur une écriture algébrique de la logique des propositions. Alors que Boole "importait" un calcul dans la logique, MacColl manifeste l'intrication des deux disciplines en prouvant leur dépendance mutuelle. Il développera ensuite ses calculs dans une voie alors nouvelle en envisageant des logiques modales et multivalentes, faisant ainsi œuvre de pionnier. On ne peut que regretter qu'il soit maintenant quasiment inconnu hors des cercles spécialisés malgré ses grands mérites.

5- Venn et Carroll successeurs de Boole

John Venn (1834-1923), mathématicien, est enseignant de science morale à Cambridge. Dès qu'il en a connaissance, il adhère à la vision booléenne de la logique qu'il défendra toujours. Il tente par contre de présenter les calculs logiques d'une manière indépendante du calcul mathématique dans son ouvrage "Symbolic Logic" en 1881, bien après la mort de Boole.

C’est l'idée de décomposition de l'univers du discours, déjà utilisée par Jevons, qui lui permit de présenter une méthode graphique de résolution des problèmes logiques à l’aide de diagrammes. Là où Boole introduisait un Calcul Symbolique sur des actes de pensée, Venn considère, dans un univers du discours, des classes d'objets sur lesquelles il définit des opérations qui sont la juxtaposition (qu'il nomme "aggregation"), l'intersection et la négation. Les notations et les lois de son calcul sont alors exactement les mêmes que chez Boole. En effet, pour ne pas prendre en compte deux fois les éventuels éléments communs à deux classes lors de la juxtaposition, l'addition se retrouve être, comme chez Boole, exclusive.

Venn reste cependant attaché aux opérations inverses, jusque dans sa critique de Jevons, lui reprochant :

Pour définir tant la soustraction que la division des classes, Venn se place d'emblée au niveau du sens. Les écritures x-y et x/y sont introduites comme notant des classes qui existent à condition que les classes x et y aient certaine relation entre elles puisqu'il s'agit d'un "inverse process". La signification est alors première et les règles de calcul y sont subordonnées. Concernant la soustraction par exemple :

A propos de la division, « inverse operation in respect to multiplication », il n'est pas moins clair :

C'est cette classe qui est notée x/y.

Pour Venn, le symbole n'a plus la même signification que chez Boole, ce n'est qu'une notation et il est ainsi porteur de sens. Il n'est plus question dès lors de transfert où d'Algèbre Symbolique. La séparation radicale entre calcul et signification, si problématique, a disparu :

Cette économie existera d'autant plus que, grâce à la nature de ses objets, le système est rendu visuel par une représentation en diagrammes.

Le support en est des "compartiments réciproquement exclusifs et collectivement exhaustifs" (compartments mutually exclusive and collectively exhaustive), où l'univers du discours est partagé en régions deux à deux disjointes (au nombre de 2ⁿ lorsqu'il y a n classes), par dichotomie, prenant en compte toutes les situations possibles. Au bout du processus de calcul sur les classes, tout problème fait apparaître trois sortes de régions dans le diagramme :

Celles qui sont nécessairement vides, et qui seront hachurées.
Celles qui ne sont pas vides, marquées d'une croix.
Celles pour lesquelles on ne sait rien, qui ne reçoivent pas de marque.

Ce qui est apparu graphiquement n'est alors que la représentation de la situation des classes, permettant de répondre aux questions posées dans le problème, ce qui n’est pas forcément le plus simple. "Ceci manifestera pour les yeux, en un coup d'œil, le contenu complet des propositions prises collectivement." [Venn 1881, p.123]

Figure 2  Diagramme de Venn [Venn, 1881, p. 271]

Il est bien clair qu’alors la référence aux diagrammes n’est pas faite pour donner une légitimité géométrique aux calculs, mais bien pour prendre en compte les données du problème qui sont visualisées et peuvent se cumuler progressivement (successive increment of knowledge) dans une figure d’une manière simple et pratique. La représentation graphique des classes ajoute même souvent de la fluidité au traitement booléen en permettant d'éviter certains calculs qui peuvent ainsi rester implicites.

Venn utilise une vision analytique de l’univers du discours clairement conçu comme formé de compartiments disjoints (représentant des portions de classes) dont certains peuvent être vides, ce qui sous-tendait implicitement la méthode de Jevons. Mais le travail de Venn n'est pas une traduction de Jevons en diagrammes, puisque Venn s’inscrit dans la continuité algébrique de Boole, (même s'il a changé les objets du calcul et donc le calcul lui-même) alors que Jevons se situe dans une tradition différente où l’essentiel est d’assurer la prééminence de la philosophie sur les mathématiques. Ils donnent cependant tous deux, chacun à sa manière, un prolongement à l’avancée de Boole en rendant opérationnel un arrière plan de type ensembliste qui, masqué par le traitement essentiellement opératoire des données, n’apparait pas chez Boole. Ce sont les diagrammes de Venn qui sont utilisés dans l'enseignement élémentaire de la théorie des ensembles.

Dans la continuité de Venn, Charles Dogdson, (1832-1898), lui aussi enseignant de mathématiques, plus connu sous le pseudonyme de Lewis Carroll, transforme la logique en jeux d’enfants, principalement grâce à l’utilisation de diagrammes proches de ceux de Venn (où cependant l'univers du discours est plus prégnant) en particulier dans The game of Logic en 1886. Cet ouvrage était vendu avec un tableau en carton figurant un diagramme (cf les compartments de Venn) et des jetons de deux couleurs pour y marquer certaines cases. Le lecteur était ainsi invité à jouer au logicien. Dans Symbolic logic l'année suivante, il fera preuve de virtuosité dans l'utilisation de ses diagrammes pour résoudre des problèmes logiques complexes présentés de manière humoristique. On peut considérer qu'alors le système mis au point par Boole (mais fortement remanié) est en passe de rentrer dans les mœurs.

6- Extensions

Dans le même temps, la graine booléenne avait germé outre-atlantique et c’est en fait toute une école qui voit le jour aux U.S.A. autour de Charles Saunders Peirce (1839-1914). Si Peirce est réputé comme l’un des fondateurs de la sémiotique, qui résulte de ses études sur les signes et leur statut, c’est à travers la filiation booléenne qu’une telle préoccupation l’atteint. Il est aussi utile de remarquer que C. S. Peirce est le fils du mathématicien Benjamin Peirce (1809-1880) qui publia en 1875 Linear associative algebra dont l’idée de base est le développement d’algèbres à partir des quaternions.

Dès 1867, C. S. Peirce intervient en logique avec un article dont le titre donne l’orientation : "On an improvement in Boole’s calculus of logic", et d’autres suivront dans la même période. Ses réflexions vont se préciser dans un article de 1870, "Description of a notation for the logic of relatives", où il introduit pour la première fois comme symbole de base l’inférence, qu’il note " ?< ". Son objet est de prolonger le calcul booléen à l’étude des relations, à la suite des travaux de De Morgan sur ce sujet, et ses notations, complexes voire surprenantes, sont parfois proches de ce dernier. On y trouve en particulier une notation matricielle pour rendre compte de la composition des relations. Il continuera ses contributions par deux articles de même titre "On the algebra of logic" en 1880 et 85. C’est dans le second de ces articles qu’il introduit la quantification, dont il attribue le mérite à un de ses élèves, Oscar Mitchell (1851-1889). La quantification universelle est notée par un produit, puisqu’elle correspond à une conjonction, alors que l’existentielle, liée à la disjonction, est notée par une somme.

En 1883, à l’initiative de Peirce, c’est un recueil d’articles de différents auteurs intitulé "Studies in logic by members of the John Hopkins University" qui permet d’exposer certains aspects de la recherche autour des calculs booléens hors des revues spécialisées. Une de ses élèves, (enfin une femme dans cette histoire !) Christine Ladd-Franklin (1847-1930), y développe un système de calcul booléen basé sur un seul connecteur "aucun A n’est B". C'est la manifestation que la place des femmes dans la société évolue aussi. Les études universitaires commencent à leur être accessibles, et elles commencent à y être reconnues, mais tout n'est pas encore gagné, et le combat sera rude. (cf. Mary Sommerville, Ada Lovelace, Sophie Germain, Sofia Kovalevskaia, Marie Curie, Emmy Noether . . .)

Figure 3 Table des matières de Studies in logic by members of John Hopkins University [Peirce, C. S., 1883]

En fait, à partir des années 1870, il se produit une sorte d’explosion de publications portant sur la logique dans de nombreux pays, qu’il s’agisse de manuels didactiques ou de travaux de recherche. Elles sont toutes, plus ou moins, en relation directe avec les résultats de Boole, et il semble qu’un mouvement soit lancé qui ne s’arrêtera pas. Rendre compte dans le détail des motivations, du contenu, des résultats et des avancées de chacun des auteurs ne serait pas raisonnable ici. Les notations ne sont pas encore fixées et changent d’un auteur à l’autre, voire entre deux publications du même auteur suivant le sujet traité, et le vocabulaire lui non plus n’est pas stable. De plus certains articles sont parfois confus et leur pertinence n’est pas très évidente pour nous, mais leur existence est une preuve de plus de l’intensité des activités de recherche et de l'intensité des débats.

Tout au plus peut-on indiquer les principales productions en soulignant les traits les plus marquants, sans aucun souci d’exhaustivité.

Rappelons le traité de Bain en deux volumes de 1870, traduit en français en 75 et en polonais en 78.

En 1874, Jevons donne Principles of science qui est un développement en quatre livres de ses travaux dans le sens de la logique inductive de Mill, sur l’ensemble de la science.

En 1877, deux ouvrages importants: Ernst Schröder (1841-1902), Der Operationskreis des Logikkalkuls à Karlsruhe, (sur lequel nous devrons revenir) et MacColl, Calculus for equivalent statements, à Londres, que nous avons déjà rencontré.

En 1879, le livre de MacFarlane (1851-1913) à Edinburgh Principles of the algebra of logic contient un chapitre entier "On Boole’s general methode".

En 1881, outre Venn et sa Symbolic logic, deux traités se réfèrent à De Morgan et Jevons dans leur préface, mais pas à Boole qui n’est cité que dans le texte. Il s’agit de Practical logic de D. S. Gregory (1822-1915), (Lake Forest University, Illinois)) qui ne contient aucun calcul et Studies and exercices in formal logic de Keynes (1852-1949) à Cambridge, qui aura une grande diffusion et de nombreuses éditions. Malgré de nombreuses citations de différents auteurs tant britanniques qu’allemands, cet ouvrage ne contient lui non plus aucun calcul. On voit donc que l’algèbre de la logique n’est pas parue nécessaire à tous. En 1884 paraît la traduction anglaise de la Logik de Lotze, (1817-1881) dix ans après son édition à Göttingen et plusieurs éditions allemandes. En 1885, c’est un élève de R. Hamilton, Veicht (1829-1884) qui publie à Edinburgh Institutes of logic, gros livre d’enseignement qui reste traditionnel.

En 1890, Schröder donne le premier des trois gros volumes de son monumental traité : Vorlesungen über die Algebra der Logik dont la publication se terminera en 1905, donc après la mort de l’auteur. Il s’agit d’une somme sur la logique "algébrique" à la fin du XIX° siècle où Schröder rassemble ce qui existe dans une sorte d’état des lieux, qui mériterait à elle seul une étude. Cet ouvrage, qui marque une étape, eut une influence considérable sur le développement de la logique au début du XX° siècle.

La vague atteindra même l’orient puisqu’à Kazan, Platon Poretskiy (1846-1907) étudiera la résolution des équations booléennes, ainsi que les égalités et non-égalités logiques et publiera, dès 1881, en partie en français, ses résultats, positifs, sur ces sujets.

7- Du côté de l'Allemagne

En Allemagne, la situation aurait pu être désespérée après que Emmanuel Kant (1724-1804) ait déclaré que la logique était achevée, ce qui aurait pu signifier sa fin, mais Friedrich Hegel (1770-1831) l’a ressuscitée sous le nom de métaphysique. Les débats étaient réels sur ces questions philosophiques au milieu du siècle, tout comme le développement des problèmes mathématiques et leur extension dans les universités allemandes. Il s'agissait de savoir comment les mathématiques, installées à la base du système, pouvaient participer à une médiation entre connaissance pure et démarche expérimentale de l'industrie. Dans ce cadre, des traités sont publiés qui marquent un regain d’intérêt pour la discipline logique. Par exemple, en 1840 Trendelenburg, philosophe, (1802-1872) développe le point de vue de Hegel dans Logische Untersuchungen. En 1851 Drobisch, (1802-1896) professeur de mathématiques et philosophie à l’université de Leipzig, publie Neue Darstellung der Logic, manuel de logique traditionnelle mais comportant une partie mathématique, qui trouvera un certain écho. Il faut souligner aussi que dès 1855, (l'année suivant Les lois de la pensée), Hermann Ulrici (1806-1884), philosophe de Halle, auteur en 1852 d'un System der Logik, donne un compte rendu de l’œuvre de Boole dans une revue de philosophie allemande, ce qui montre que les discussions d'alors n'étaient pas limitées à un cercle fermé, mais il est difficile de mesurer l'influence réelle de ce compte rendu dans les débats. Puis en 1857, Ueberweg (1826-1871) produit System der Logik und Geschichte der logischen Lehren, traduit en anglais en 1871. Un dernier exemple est celui de Aloïs Riehl, (1844-1924) philosophe de l'université de Graz. En 1877, il contribue à la diffusion de la logique symbolique par son ouvrage Die englische Logik der Gegenwart qui se réfère beaucoup à Jevons. On constate ici l'absence de participation de mathématiciens à ces écrits logiques, mais peut-être étaient-ils alors occupés par d'autres problèmes ? Felix Klein (1849-1925) dans son "programme d'Erlangen" de 1872 envisage que l'adoption du point de vue choisi détermine le type de géométrie utilisée : euclidienne, non euclidienne ou projective. La même année Richard Dedekind (1831-1916) déclare que les nombres sont une "libre création de l'esprit humain" dans "Stetigkeit und irrationale Zalhen" et Georg Cantor (1845-1918) développe une théorie des nombres irrationnels suite à l'étude des séries trigonométriques dans un article des Mathematische Annalen.L'arithmétisation de l'analyse est en route.

8- Un mathématicien allemand

C'est un "géomètre" de Iena qui réalise une percée logique fondamentale, dans une direction non booléenne totalement nouvelle. Gottlob Frege (1848-1925) tente de donner à l’arithmétique un fondement logique en liaison avec les recherches développées en Allemagne concernant la nature des nombres. C’est en 1879 qu'il publie Begriffsschrift (rendu en français par Idéographie) dont le sous-titre est : Eine der arithmetischen nachgebildete Formelsprache des reinen Denkens. (Langue formelle de la pensée pure conçue à l’image de l’arithmétique). Un parallèle instructif peut être relevé :

Contre le relativisme, le psychologisme et l’utilitarisme alors très prégnants, Frege veut fonder les connaissances, et en particulier l’arithmétique, sur une base nouvelle et hors du temps : les concepts et leur extension. En moins de cent pages, c’est un bouleversement radical du paysage de la logique qui se produit. Le couple sujet-prédicat, les syllogismes, les lois de la pensée et tout ce qui gravitait autour disparaissent, pour faire place à une nouvelle approche où les premiers rôles reposent sur le couple fonction-argument et la notion de vérité. Les calculs de type algébrique cèdent la place à des schémas bidimensionnels aussi bizarres qu'impressionnants qui se combinent entre eux pour produire des théorèmes.

Figure 4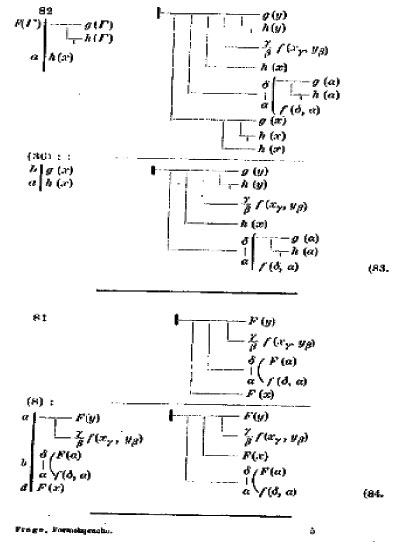 Exemple de "calcul" dans l'Idéographie de Frege [1879, p. 65]

Devant les incompréhensions de son travail, et en réponse à la critique de Ernst Schröder (1841-1902) qui, dérouté par l’ampleur du changement, ne le comprend manifestement pas, il doit se défendre et dans Sur le but de l’idéographie de 1882, (traduit en français et publié par C. Imbert avec d'autres articles de Frege dans Ecrits logiques et philosophiques en 1971, noté ELP dans la suite) il tient à préciser :

Si Frege se distingue résolument de la voie suivie par Boole en refusant le caractère aveugle de l'écriture algébrique, il y a continuité puisque tous les deux vont investir des objets mathématiques en tant qu'absolus : le symbole algébrique pour Boole et la vérité manifestée par la notion de fonction pour Frege.

Rompant avec une vision formelle, il s’agit pour Frege d’établir une technique de calculs fondée sur les concepts et leurs relations, donc sur le sens, le traitement de l’ensemble étant fonctionnel. Ainsi, la proposition classique ‘Si Socrate est un homme, alors Socrate est mortel’ est comprise comme le résultat de l’application de la fonction : ‘Si . . . est un homme, alors . . . est mortel’ à l’argument Socrate, et la valeur prise alors par cette fonction est ici le vrai. Concernant les propositions, qui sont toutes assimilées à des conditionnelles, les deux outils de base sont l’implication et la négation Ces deux transformations, déjà mises en évidence par MacColl, dans un contexte bien différent, semblent alors avoir définitivement conquis leur place au cœur du calcul propositionnel. La vision totalement nouvelle des objets logiques s’accompagne d’une sorte de représentation sténographique originale à deux dimensions très lourde à utiliser et qui, de ce fait, n’a pas résisté à l’épreuve du temps. Frege explique son invention graphique :

En outre, l’émergence d’une vision purement fonctionnelle offre enfin la possibilité de distinguer entre la fonction elle-même, la valeur qu’elle renvoie pour un argument donné, et l’ensemble des valeurs prises pour l'ensemble des arguments possibles, comme elle permet de séparer un concept de son extension qui lui est secondaire. C’est ce qui permet à Frege la mise en place d’une véritable quantification qui est encore la nôtre, même si sa notation en diffère beaucoup. Le résultat qui découle de ces travaux est le calcul des prédicats (au nouveau sens fonctionnel du terme) avec la quantification, c’est à dire la logique du premier ordre.

Figure 5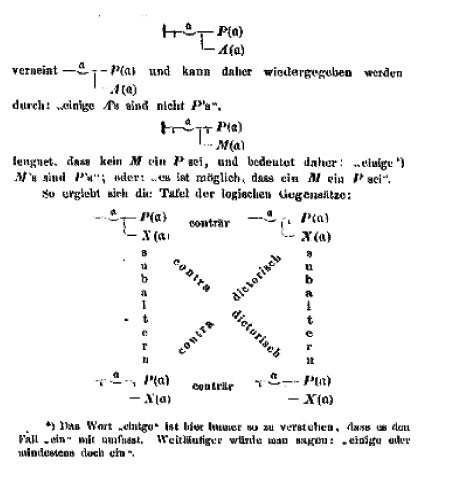 Quantification et carré logique chez Frege [1879, p. 24]

De plus, dans ses interventions postérieures, en grande partie justifiées par les réactions rarement bienveillantes à son travail, Frege continuera sur la voie de l’analyse fine de notions considérées comme communes (par exemple ses articles "Fonction et concept", "Sens et dénotation", "Concept et objet", "Qu'est-ce qu'une fonction ?" accessibles dans "Ecrits logiques et philosophiques" déjà cité) sans concession aucune, jetant les bases d’une logique sémantique solide. Le paysage de la logique est radicalement transformé par l’émergence de ce nouveau continent : à côté du calcul booléen dans lequel il s'agissait de résoudre des équations, il y a maintenant l’Idéographie fregéenne où l'essentiel repose sur la valeur de vérité de certaines fonctions; la logique comme calcul se trouve confrontée à la logique comme langage ...

9- Un autre

Le problème récurrent des algèbres sera une des motivations de Ernst Schröder (1841-1902) dont le but avoué est, à travers la mise au point de l’algèbre de la logique (qui est pour lui une sorte de brouillon), d’établir les lois de l’algèbre la plus générale qui soit. Dès 1874, ses préoccupations sur le sujet donnent un écrit : Über die formalen Elemente der absoluten Algebra. C’est la lecture des frères Grassmann qui attire son attention sur les liaisons entre algèbre et logique, et c’est à ce moment qu’il s’intéressera aux travaux alors un peu anciens (Boole, De Morgan,...) et plus modernes (Trendelenburg, Peirce, ...). Un des points mis en avant en 77 dans Der Operationskreis des Logikkalkuls et systématisé plus tard dans Vorlesungen über die Algebra der Logik est la dualité entre addition et multiplication qui lui permet de présenter les résultats et les démonstrations sur deux colonnes en vis à vis, l'une concernant l'addition et l'autre la multiplication. Mais il est d’autres points importants dans les trois volumes de son énorme traité. Il reprend l’idée de Peirce et MacColl (mais aussi de Frege) d’utiliser l’inclusion (appelée alors "subsomption") comme symbole fondamental à la place de l’égalité, et adopte pour cela une notation personnelle : un symbole d'égalité traversé par une sorte de petite parabole (qui ressemble au symbole que nous utilisons pour l'euro).

Figure 6 Inclusion et dualité chez Schröder [1890, p. 167 et 276]

Le tome 1 des Vorlesungen (après une introduction de près de 130 pages !) est entièrement consacré à l’exposé d’une manière axiomatique du système booléen muni de la 'bonne' addition et débarrassé de ses insuffisances. Ce qui en constituait les faiblesses, en particulier la méthode d’élimination avec ses coefficients choquants, a disparu pour faire place à une construction rigoureuse de la solution générale du problème. Mais l’ambition est autre : le calcul exposé ne vaut pas seulement pour les classes mais se veut tout à fait général.

Figure 7 Les applications du calcul logique selon Schröder [1890, p. 160]

Il est à remarquer que tout au long des développements, le texte se présente sous une double forme, des remarques et considérations jugées secondaires, parfois d’une longueur conséquente, étant insérées en caractères plus petits, ce qui permet une lecture à deux niveaux. (On peut noter qu’il s’agit d’une amélioration, qui semble alors assez répandue en Allemagne, d‘un procédé du même ordre existant déjà dans l’Organon de Lambert où ce qui est jugé plus important est mis en évidence par des caractères plus gros.) Le tome 2 en deux parties (1891-1905) expose le calcul propositionnel où Schröder reprend l’idée de Boole de considérer comme marqueur, le temps durant lequel une proposition est vraie. Il ramène ainsi le traitement des propositions à un calcul de classes et il compare les deux, retrouvant l'équivalence établie par Boole. On y trouve aussi un exposé de la quantification. Mais ce n’est pas chez Frege qu’il va chercher ce concept, mais encore une fois, chez Peirce, dont il adopte les notations sous forme de Π pour la quantification universelle et Σ pour l’existentielle. Le tome 3 contient le calcul des relations, avec de nombreux développements pas toujours très évidents, mais dans la continuité des études de De Morgan et Peirce.

A la lecture, autant les exposés de Peirce peuvent paraitre simples en apparence et parfois sommaires, autant le travail de Schröder est méticuleux et précis. On sent un souci constant d’exposer tous les détails qui se présentent de façon à ne rien laisser dans l’ombre et les contributions de chacun sont exposées et comparées entre elles. Ce qui s’était construit, à la suite de Boole, par un effort collectif durant des décennies, est analysé, synthétisé, mis en forme et exposé globalement pour la première fois.

Malheureusement, il est dommage que tout ce travail soit arrivé en quelque sorte trop tard, après la bataille, car à la toute fin du siècle, le problème n’était plus de défendre la logique sous sa forme algébrique, mais bien de l’utiliser pour expliquer comment les mathématiques peuvent exister et rendre compte du monde.

10- Quel bilan?

Cet aperçu montre à la fin du XIX° siècle un foisonnement des travaux logiques quant à leur nature, et l’on voit que les calculs de Boole n’ont pas forcément gagné la partie, tant le poids de vingt siècles de pensée structurée autour du langage est forte dans les pays où la logique de l’Ecole était une tradition comme l’Angleterre et l’Allemagne. On peut aussi s'étonner de l'absence totale, et non encore élucidée, de toute contribution française. Pourtant Louis Liard (1846-1917), qui enseigne la philosophie à l’université de Bordeaux, après avoir exposé les travaux de Boole et Jevons dans deux articles en 1877, publie Les logiciens anglais contemporains en 1878, qui sera traduit en allemand en 1880. Malgré ces efforts, qu'il poursuivra, (quand il sera à la direction de l'enseignement supérieur, il enverra Louis Couturat (1868-1914) étudier à Hanovre les manuscrits logiques de Leibniz), il faudra attendre plus que le début du XX° siècle pour que la logique soit considérée comme un sujet digne d’étude en France. Mais cependant, les idées semées font leur chemin et se répandent sur une aire géographique qui ne cessera de croitre. Des nations nouvelles, et pour certaines nouvellement crées, apportent des contributions non négligeables à l’effort de développement qui devient ainsi collectif. A travers l’échange de correspondance et la lecture d’articles dans les revues professionnelles qui sont toujours plus nombreuses, une communauté de logiciens se crée peu à peu, soudée par les efforts faits pour étendre toujours plus l’intervention de leur discipline, principalement en mathématique, en même temps qu’ils tentent d’en assurer les bases. Car ce sont des mathématiciens qui s’impliquent dans le renouveau, alors que les philosophes restent, pour la plupart d’entre eux, dans l’ère pré-booléenne, comme on le voit au niveau des publications. Le renversement prôné par Frege de fonder l'arithmétique, puis l'ensemble des mathématiques, sur la logique, ne fera dans un premier temps que compliquer le débat à un moment où les remaniements faits sur le système booléen l'avaient fait à peu prés accepter. Il n'est qu'à voir la réaction de rejet de Schröder qui n'envisage pas de quitter l'algèbre. Boole se situait résolument du côté de la syntaxe par la primauté du symbole, mais Frege ouvre la voie à une expression sémantique de la logique à travers la notion de vérité. Par son attachement à la signification, il traduit un déplacement des tensions dans les mathématiques. Ce n'est plus du statut des calculs mais des relations entre les objets d'étude dont il s'agit. A travers des recherches de plus en plus précises, la notion de fonction se trouve interrogée quant à son pouvoir de reproduction, de transformation et de mise en relation d'objets. C'est elle qui finalement sera une des clefs : on passera de la simple application des processus acceptés comme une donnée, le monde des calculs, à l'examen du processus lui-même et de ce qu'il produit, le monde des structures. Le résultat en sera l'ancrage des mathématiques sur la base d'une nouveauté qui s'est peu à peu imposée : la théorie des ensembles qui est constamment restée en arrière plan. Il ne reste plus qu'à montrer qu'elle joue bien son rôle unificateur.

Pour cela, tout un langage nouveau est en train de se créer et ceci ne pourra être achevé qu’en s’appuyant fortement sur tous les acquis du XIX° siècle. C’est dans ce but que Giuseppe Peano (1858-1932) crée à Turin la "Rivista di mathematica" en 1895, et y publie son "Formulaire de mathématiques". Bertrand Russell (1872-1970) et Alfred North Whitehead (1861-1947) marqueront par leur "Principia mathematica" en 1910 l’apogée d’une nouvelle période, mais il s’agit d’une autre histoire.

Figure 8 Les axiomes de Peano pour l'arithmétique [Peano, 1902, p. 8]

Bibliographie

Boole, George (1854). An investigation of the Laws of Thought on which are founded the Mathemetical Theories of Logic and Probabilities, Walton & Maberly, Londres.

Durand-Richard, Marie-José (2006). "Opération, fonction et signification de Boole à Frege", Cahiers critiques de philosophie n° 3 , Hermann Paris

Frege, Gottlob (1879). Begriffsschrift, Louis Nebert, Halle

Frege, Gottlob (ELP. 1971). Ecrits logiques et Philosophiques. Trad. et intro de C. Imbert, Seuil, Paris

Hamilton, William R. (1853). Discussion on philosophy an litterature, education and unversity reform, Hoper and Brothers, New York

Jevons, William Stanley (1864). Pure Logic, E. Standford, Londres

MacColl, Hugh (1878). "The calculus of equivalent statements" (Third paper), Proceedings of the London Mathematical Society, Vol. 10, p. 16-28

Mill, John Stuart (1883). A System of Logic Ratiocinative and Inductive,  Harper and Brothers, 8e édition, New York.

Peano, Giuseppe (1902). Arithmetica Generale, Ditta, Paravia &co, Torino

Pierce, Charles S. (1867). "On an improvement in Boole’s calculus of logic", Proceedings of the American Academy of Art and Science, Vol 7, p. 250-261.

Pierce, Charles S. (1870). "Description of a notation for the logic of relatives", Memoirs of the American Academy, Vol. 9, p. 313-378

Pierce, Charles S. (1880). "On the algebra of logic", Am. Journ. of Math., Vol.3, p. 15-37

Peirce Charles S. (1883) , editor, Studies in Logic: By Members of Johns Hopkins University, Little, Brown and Company, Boston

Peirce, Benjamin (1870). "Linear associative algebra", Am. Journ. of Math., Vol. 4-1, p. 97-229

Schröder, Ernst (1874), Über die formalen Elemente der absoluten Algebra, Schweizerbart'sche Buchdrukerei, Stuttgart

Schröder, Ernst (1890), Vorlesungen über die Algebra der Logik, Druck und Verlag von B. G. Teubner, Leipzig. Tome1

Venn, John (1881). Symbolic Logic, Macmillan and co., Londres