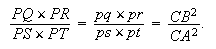De plus, il est un peu étonnant que Newton ait toujours considéré ce problème comme équivalent à celui de tracer une conique par cinq points, en supposant (tacitement) qu'une région du plan soit choisie par avance. C'est une attitude bien différente de celle qui anime les discussions entre Descartes, Roberval, van Schooten et Huyghens sur l'existence de deux solutions.
Utilisation en classe - Ce texte très riche, dans lequel toutes les démonstrations sont soigneusement détaillées, permet une immersion dans les méthodes mathématiques mises en œuvre par les « Anciens », reprises et poursuivies ici par Newton, pour traiter certaines questions liées aux Sections Coniques.
Certains passages de ce texte pourraient certainement être lus et commentés en classe préparatoire pour donner une perspective historique à l’étude des Coniques.
Les professeurs de mathématiques du secondaire trouveront pour leurs élèves quelques situations de problèmes géométriques impliquant les rapports de longueurs, les angles, et bien sûr les triangles semblables. En particulier, le problème de Pappus dans le cas du cercle, qui fait l’objet de la Section 4, offre une configuration exploitable en classe de seconde.
Version [pdf ] (1.8 Mo, 24 p.).
SOMMAIRE
1 . Introduction
3. La construction organique des coniques
4. Newton et le cercle de Descartes
5. La Veterum loca solida constituta
6. La Solutio problematis Veterum de loco solido
6.2 Les théorèmes mis en œuvre
6.3 Une comparaison avec les Principia
9. Conclusion
L'intérêt pour le problème de Pappus parcourt toute la carrière scientifique de Newton. [1] Bien qu'il ait donné des contributions considérables aussi au cas général, [2] c'est surtout au cas de quatre lignes qu'il a réservé la plus grande attention.
Rappelons la formulation de ce problème dans le cas de quatre lignes. [3]
|
Figure 1
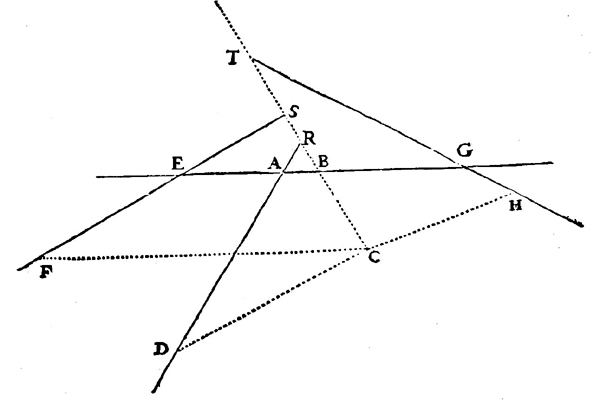 Le problème de Pappus |
Les droites EF, AD, AB, GH sont données avec quatre angles qui sont donnés en même temps.Il s'agit de déterminer le lieu des points C tels que, en conduisant les lignes CF, CD, CB, CH, sur EF, AD, AB, GH suivant les angles donnés, la raison de CB × CD à CF × CH soit donnée. On voit immédiatement que les points d'intersection E, G et les points d'intersection de AD, EF, et de AD, GH qui ne sont pas indiqués dans la figure de la Géométrie de Descartes que j'ai reproduite) sont des points du lieu.*
La solution (analytique) du problème de Pappus est une sorte de « fil rouge » qui relie les trois livres de La Géométrie de Descartes et dont Descartes était à juste titre très fier. Newton, après ses années d'apprentissage toutes «cartésiennes», devient de plus en plus critique envers l'utilisation exclusive des outils algébriques pour résoudre les problèmes géométriques. Dans le cas de quatre lignes il oppose à la solution cartésienne [4] une pluralité de solutions qui poursuivent l'idéal de retrouver la solution «parfaite» possédée, à son avis, par les Anciens.
Le problème de Pappus dans le cas de quatre lignes est considéré par Newton comme équivalent à la détermination d'une conique passant par cinq points. Puisqu'il suppose toujours (implicitement) que l'on doit chercher la solution dans une région donnée du plan, il ne pose jamais la question de l'existence de deux solutions, question qui était l'objet d'un âpre polémique entre Descartes et ses adversaires. [5]
La première solution du problème de Pappus à quatre lignes, opposée a celle de Descartes, est donnée par Newton au moyen de sa célèbre construction organique des coniques, envoyée à Collins (sans démonstration) dans la lettre du 20 août 1672. [6] Cette solution est reprise plusieurs fois. Dans la Solutio Problematis Veterum de Loco Solido [7] elle est donnée après la solution newtonienne du problème de Pappus. La démonstration aussi dépend de la solution donnée à ce problème.
La construction organique est donnée de façon semblable dans le De Motu. [8]Enfin dans les Principia [9] on a la formulation classique. Dans la Section 3 nous donnerons la description de cette construction et expliquerons son usage pour construire une conique par cinq points. La démonstration de Newton sera exposée dans la Section 6.
Toutefois dans les années qui suivent la solution du problème de Pappus par la construction organique, Newton s'est arrêté de façon détaillée sur le cas particulier du problème de Pappus où la solution est donnée par un cercle. C'est l'exemple choisi par Descartes dans La Géométrie. [10] Probablement Newton projetait de considérer ce cas particulier à l'intérieur d'un traité de géométrie élémentaire, mais ce traité, comme la plus ambitieuse Geometria de sa vieillesse n'a jamais vu le jour. [11] Dans la Section 4 nous proposons une démonstration possible du résultat indiqué par Newton.
Dans la Veterum Loca solida Restituta [12] une construction intéressante d'une conique par cinq points est donnée, accompagnée d'une piquante critique envers Descartes. Après avoir observé que Descartes a eu tort de prétendre avoir donné une solution inconnue par les Anciens [13] il observe :
Avec tout le respect dû à un si grand homme, je croirais que cette chose n'a nullement été ignorée des Anciens. Pappus nous enseigne en effet une méthode pour décrire une ellipse par cinq points donnés, et le raisonnement est le même pour les autres coniques. Et si les Anciens savaient décrire une conique par cinq points donnés, qui peut ne pas voir qu'ils connaissaient la composition du lieu solide ? [14]
Des critiques semblables envers Descartes accompagnent tous les textes où Newton s'occupe du problème de Pappus. Nous ne rendrons pas compte de ces critiques bien qu'elles soient du plus grand intérêt surtout lorsqu'elles se prolongent par des considérations méthodologiques. [15] Les résultats contenus dans la Veterum Loca solida Restituta sont exposés dans la Section 5.
La Solutio Problematis Veterum de Loco Solido est un texte plutôt élaboré, qui, après la révision dans le De Motu, constitue la base de la Cinquième Section du Premier Livre des Principia. [16]
Dans la Section 6 nous donnerons un exposé détaillé de la partie la plus importante de ce texte et dans la Sous-section 6.3 nous ferons une comparaison avec les Principia.
La composition de la Arithmetica Universalis [17] se place chronologiquement entre la Solutio Problematis Veterum de Loco Solido et le De Motu. Du point de vue de la « Geometria Veterum » on n'a pas de grandes choses. Mais il y a une solution vraiment «cartésienne» du problème de Pappus. Nous exposerons cette solution dans la Section 7.
Dans les deux dernières Sections nous effleurerons les idées de Newton qui, à partir du problème de Pappus acquièrent une importance méthodologique considérable.[18]
2- Prémisses classiques
Newton a toujours considéré les propositions III.17-III.19 des Coniques d'Apollonius et les propositions VIII.13, VIII.14 des Collections de Pappus comme une connaissance de base avec laquelle son lecteur devait être familier.
Nous nous limitons ici à présenter le contenu de la III.17 des Coniques. [19]
|
Figure 2
 La proposition II.17 d'Apollonius |
3- La construction organique des coniques
Comme nous l'avons déjà écrit dans la Section 1, cette construction est exposée dans une lettre à Collins de 1672. [21] On peut la décrire facilement à l'aide de la Figure 3 suivante.
|
Figure 3
 La construction organique des coniques 1 |
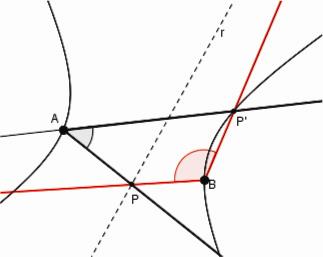
Cette construction nous donne immédiatement la possibilité de tracer une conique de laquelle cinq points sont donnés (voir la Figure 4 suivante). Supposons qu'une conique soit donnée par les points A, B, C, P, Q et considérons les trois points A, B, C. Ces points déterminent les angles BAC, ABC qui peuvent être utilisés comme angles tournants autour des sommets A, B. Si l'on tourne ces angles de façon que deux des leurs côtés se coupent au point P, les autres côtés par leur intersection donneront le point P'. En utilisant le point Q on obtient le point Q' et donc la ligne P'Q'. Il est facile de voir (puisque une conique est déterminée par cinq points) que à partir de cette ligne par le moyen de la construction organique avec les angles BAC, ABC et les pôles B, C on trace la conique par les cinq points donnés. [22]
|
Figure 4
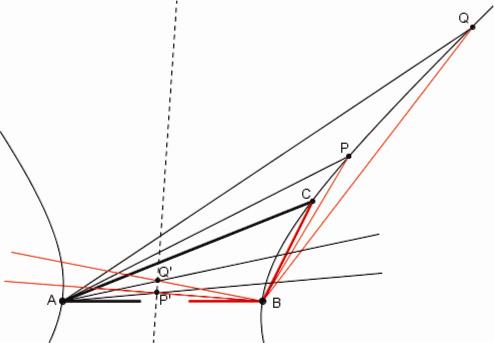 La conique par cinq points |
4- Newton et le cercle de Descartes
Dans (MP, vol.4, p. 230-269) Whiteside a rassemblé plusieurs problèmes de géométrie élémentaire, dont beaucoup fournissent des propriétés du cercle. Ceux qui sont indexés par les nombres 12, 14, 15 correspondent à des cas particuliers du problème d Pappus. Voyons le numéro 15, que Newton énonce sans démonstration, mais pour lequel la démonstration est suggérée par le choix même des données.
|
Figure 5
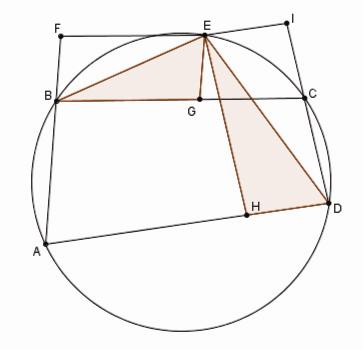 Le problème de Pappus dans le cas du cercle |
Si dans un cercle quelconque ABCD le trapèze ABCD est inscrit, et à partir d'un point arbitraire E de la circonférence l'on mène les lignes EF, EG qui forment avec les côtés AB, BC le parallélogramme EFBG et les lignes EH, EI qui forment avec les côtés AD, DC le parallélogramme EHDI, le rectangle GE x EH contenu par les lignes menées sur les côtes opposés est égal au rectangle EF× EI contenu par le lignes menées sur les côtés restants.
Toute la démonstration consiste simplement à prouver que les triangles EBG et DEH sont semblables. Évidemment ABC = BFE = BGE. L'angle CDH est supplémentaire de DHE et, puisque ABCD est inscrit dans un cercle, l'angle CDH est aussi supplémentaire de ABC. Il s'ensuit que DHE = BGE.L'angle CBE est égal à CDE et puisque EH // DI , l'on a CDE = DEH. La similitude des triangles EBG, DEH est prouvée. Il s'ensuit que BG : EG = EH : HD. Mais BG = EF, HD = EI et donc EF × EI = EG × EH.
Si l'on substitue à EF, EG, EH, EI les perpendiculaires EF', EG', EH', EI', on a évidemment
|
|
et |
|
et la même chose arrive si l'on prend les angles comme Newton |
le déclare. On est ramené au cas précédent. [24]
Remarque: Newton ne donne pas la Proposition réciproque, qui toutefois est presque évidente. Si ABCD est un trapèze qui peut être inscrit dans un cercle, et (avec la même structuration des données) EF × EI = EG × EH, le point est sur le cercle par A, B, C, D.
En fait, l'égalité DHE = BGE est donnée par la simple considération du parallélisme, et ne dépend pas de l'hypothèse que E soit sur le cercle passant par A, B, C, D . De EF × EI = EG × EH il s'ensuit que EF ( = BG) : EG = EI ( = HD) : EH et donc les triangles EBG et DEH sont semblables. Donc EBC = HED = EDC. Les angles égaux EBC, EDC sous-tendent le même segment EC et donc les points E, B, C, D sont sur un même cercle, qui ne peut être que le cercle passant par A, B, C, D.
5- La Veterum loca solida constituta
Ce bref texte est composé de deux propositions seulement, que constituent la solution de deux problèmes. [25]
Décrire une conique qui contient les trois points A, B, C et a son centre en O.
Supposons donc qu'une conique soit donnée par les trois points A, B, C et son centre O .
|
Figure 6
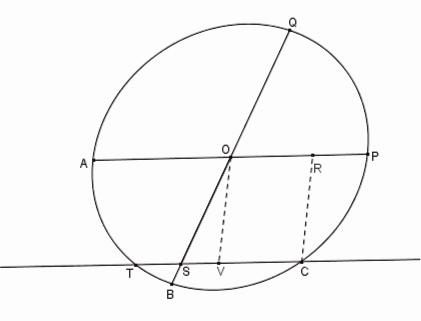 |
| (2) |
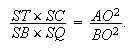
|
Il s'ensuit que le point T est déterminé et la III.17 d'Apollonius nous permet d'affirmer que ce point est sur la conique. Soit V le milieu de TC . OV donne la direction conjuguée de AP et une fois que CR est tracée parallèle à OV, le latus rectum l, relatif au diamètre AP est donné par la proportion
| (3) |
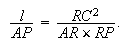
|
Le latus rectum l relatif au diamètre AP et le diamètre AP déterminent la conique.
|
Figure 7
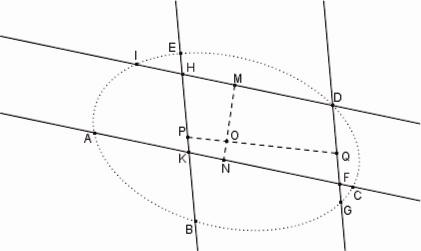 |
Joignons A, C et B, E et soit K le point d'intersection de AC et BE . DI et DG sont tracées parallèles à AC et BE respectivement. AC et DG se coupent en F ; BE et DI se coupent en H . La proposition d'Apollonius peut être utilisée encore pour localiser deux points I et G de la conique sur DI et DG respectivement. On a, en effet
| (4) |
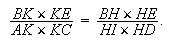
|
Puisque les points A, B, C, E, K sont donnés, le rapport
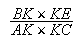
|
est donné et donc le point I est donné. De la même façon :
| (5) |
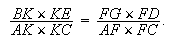
|
Le point G est donné à son tour. Soit M, N les milieux de DI, AC, et P, Q les milieux de BE, GD.
L'intersection O de MN et PQ sera le centre de la conique, et nous pouvons utiliser le résultat du Problème 1. [27]
Pour la solution de problème de Pappus il s'agit seulement de déterminer cinq points :
Après ces prémisses, il ne reste qu'à rechercher cinq points par lesquels la figure passe pour mener à bien la composition du lieu solide. [28]
Puisque quatre points sont donnés immédiatement [29] il s'agit simplement d'utiliser la condition de Pappus pour trouver un cinquième point. Puisque la solution de Newton est reprise dans la Solutio problematis Veterum de loco solido sans changements essentiels, nous la donnerons dans la Section suivante.
6- La Solutio problematis Veterum de loco solido
6.1 Les principaux théorèmes
Le texte de ce manuscrit commence par le théorème suivant. [30]
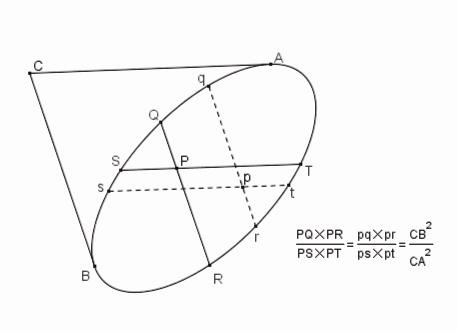
Si l'on mène d'un point P d'une conique aux quatre côtés étendus à l'infini AB, CD, AC, BD d'un quadrilatère inscrit dans cette conique un nombre égal de lignes droites PQ, PR, PS, PT qui forment chacune un angle donné avec chacun des quatre côtés du quadrilatère, le produit PQ × PR de deux lignes menées sur deux côtés opposés sera en raison donné au rectangle PS × PT des droites tirées aux deux autres côtés opposés. [31]
La démonstration est conduite en considérant trois cas, dans un style qui évoque la stratégie utilisée (selon notre reconstruction) pour le problème du cercle (on peut voir la Section 4).
|
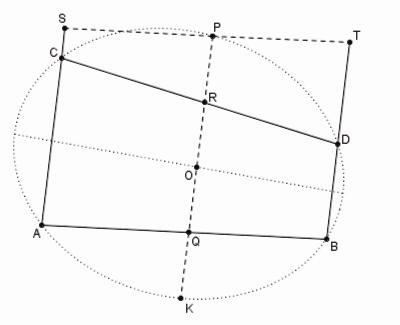
Figure 8
|
Supposons au début que les côtés AC, BD soient parallèles et que PR, PQ soient à leur tour parallèles à BD pendant que PS, PT sont parallèles à un autre côté, par exemple AB, comme sur la Figure 8.
La droite qui passe par les milieux de A, C et B, D est un diamètre. Soit O le point d'intersection de ce diamètre avec PQ . PO sera une ordonnée à ce diamètre, puisque sa direction est celle conjuguée. Si l'on prend OK = PO dans la direction opposée on a un autre point K de la conique.
| De la III.17 d'Apollonius il s'ensuit que le rapport |
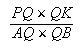
|
est donné. |
Mais OQ = OR, QK = PR et par conséquent, puisque
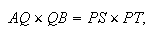
|
il s'ensuit que
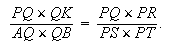
|
| Le rapport |
|
est donc donné. |
Voyons le second cas. Les côtés AC et BD ne sont plus parallèles, mais PR, PQ sont encore pris parallèles à AC, pendant que PS, PT sont pris parallèles à AB.
|
Figure 9
 Proposition 1 : Le second cas |
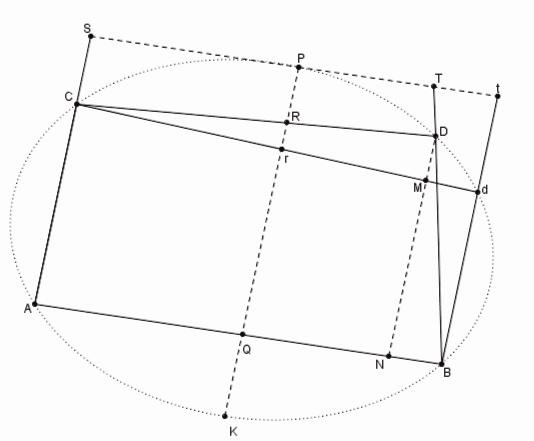
Le triangle BTt est semblable au triangle DBN.
Il s'ensuit que Bt : Tt = DN : BN. Mais Bt = PQ, et donc PQ : Tt = DN : BN.
Puisque Rr : DM = CR : CD = AQ : AN et AQ = PS,
on a Rr : DM = PS : AN et Rr : PS = DM : AN.
En composant les rapports, on a
| (6) |
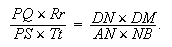
|
Si l'on considère le quadrilatère ADNC, on peut utiliser ce que nous avons démontré dans le premier cas :
| (7) |
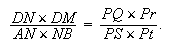
|
Puisque D est donné, la valeur du rapport au second membre ne dépend pas de la position de P. La comparaison de (6) et (7) donne
| (8) |
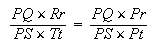
|
et donc Pr : Pt = Pt : Tt et (Pr - Rr) : Pr = (Pt - Tt) : Pt.
Puisque Pr - Rr = Pr et Pt - Tt = PT on a PR : Pr = PT : Pt, c'est à dire
| (9) |
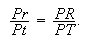
|
| Dans le deuxième membre de (7) on peut substituer au rapport |
|
le rapport |
|
et donc le rapport
| (10) |
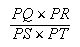
|
est donné.
Voyons le troisième cas.
|
Figure 10
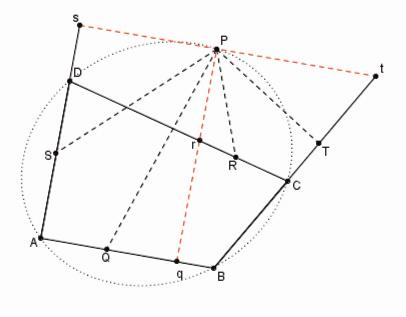
Proposition 1 : Le troisième cas
|
Sur la Figure 10, PQ, PR, PS, PT forment des angles arbitraires avec les côtés du quadrilatère (arbitraire). Mais Pq, Pr (en rouge dans la figure) sont parallèles à AD et Ps, Pt (encore en rouge sur la figure) sont parallèles à AB. Les angles des triangles PQq, PRr, PSs, PTt sont donnés et du cas
| précédent il s'ensuit que |
|
est donné. |
Mais les rapports
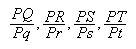 sont aussi donnés et donc le rapport
sont aussi donnés et donc le rapport 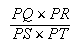 est donné.
est donné.
Remarque : Dans une étape intermédiaire de la démonstration du deuxième cas du Théorème 1, Newton
| a prouvé que |
|
. Si nous imaginons que la conique soit donnée par les points A, B, C, P, |
d cette égalité donne une caractérisation des autres points D de la conique. On a un cas particulier (puisque AC // Bd ) de la génération homographique. Le cas plus général est l'objet de la Proposition cinquième, que nous proposons avant la Proposition destinée à la détermination d'un cinquième point à partir de la condition de Pappus. [32]
Si entre les points donnés A, P d'une conique arbitraire, un parallélogramme AQPS est inscrit, [33] et si deux côtés AQ, AS sont prolongés jusqu'à couper la courbe en B et C, et qu'ensuite par les points B et C on mène les lignes BD, CD vers un cinquième point arbitraire D de la conique, et que ces lignes coupent les côtés opposés PS et PQ en T et R, la raison de PR à PT sera donnée. Et réciproquement si la raison de PR à PT est donnée, le point D sera sur une conique qui passe par les points A, B, P et C. [34]
Nous nous limiterons à proposer la démonstration de la partie directe de l'énoncé. La partie réciproque s'obtient facilement en renversant les égalités.
|
Figure 11
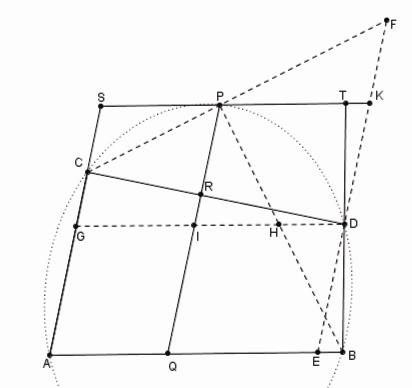
Proposition 5
|
| (11) |
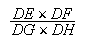
|
| est donné. Mais DE (= IQ) : PQ = HB : PB = DH : PT, c'est à dire |
|
La |
| substitution de |
|
à |
|
dans le rapport (11) montre que le rapport |
| (12) |
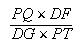
|
| est donné à son tour. On a encore DF : PR = DC : RC = DG : PS (= IG). C'est à dire |
|
| La substitution |
|
à |
|
dans le rapport (12) montre que le rapport |
| (13) |
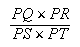
|
est donné. Mais les droites PQ, PS sont données et donc le rapport de PQ à PS est donné. Il s'ensuit que le rapport de PR à PT est donné.
Avant de voir l'utilisation de cette Proposition pour tracer une conique, voyons comment la condition de Pappus peut être exploitée pour avoir cinq points d'une section conique.
Déterminer un point P tel que, si l'on conduit les quatre lignes PQ, PR, PS, PT sur quatre autres lignes données de position AB, CD, AC, BD selon des angles donnés, le rectangle PQ × PR soit en raison donnée au rectangle PS × PT. [35]
|
Figure 12
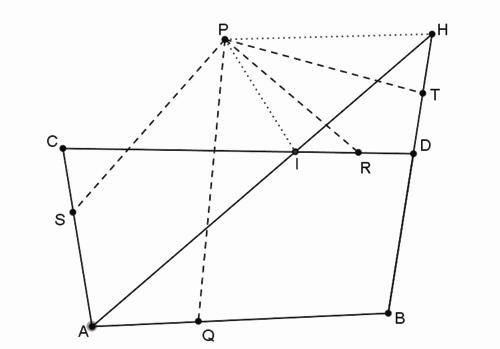 Un point de la section conique |
Supposons que les données soient celles de la Figure 12 et traçons la ligne AH par A qui coupe CD en I
|
et BD en H. Puisque tous les angles de la figure sont donnés |
|
et |
|
sont donnés, et |
| il s'ensuit que le rapport |
|
est donné. Par hypothèse |
|
est donné et |
| par conséquent le rapport |
|
est donné. |
| Puisque les rapports |
|
et |
|
sont donnés à leur tour, |
|
est donné |
[36] et enfin le point P est donné.
Tous ces résultats nous donnent une façon simple de déterminer une conique par cinq points.
Définir une section conique qui passe par cinq points. [37]
Considérons la Figure 13, qui correspond aux données du Théorème 2.
|
Figure 13
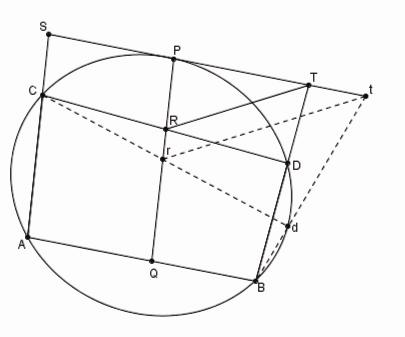 La génération homographique d'une conique |
Menons un ligne arbitraire Cr par C. Une ligne rt parallèle à RT détermine un point t sur PS tel que PR : PT = Pr : Pt. La ligne Bt coupe la ligne Cr en un nouveau point d de la section conique. En variant la ligne Cr on peut décrire tous les points de la conique. [38]
Ce théorème a un rôle stratégique très important. On peut le voir à l'œuvre dans les Théorèmes 5 et 6, pour démontrer la construction organique et pour une généralisation intéressante de la génération homographique.
6.2 Les théorèmes mis en œuvre
Si deux lignes BM, CM conduites par les points donnés B, C se coupent en un point M d'une ligne MN donnée de position et si deux autres lignes BD, CD sont menées, formant des angles donnés MBD, MCD avec les deux lignes précédentes menées par les points B, C ; je dis que les deux dernières lignes tracent, par leur intersection D un lieu solide. Réciproquement, si les lignes BD, CD tracent un lieu solide qui passe par les points B, C, G et quand ces lignes se coupent en le point G du lieu les autres deux coïncident avec la ligne BC, le point M appartiendra à une ligne donnée de position. [39]
|
Figure 14
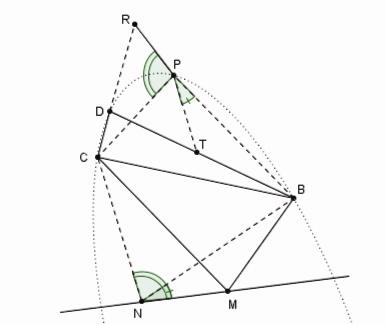 La démonstration de la construction organique 1 |
Soit donné le point N sur la ligne MN. Quand le point mobile M coïncide avec N , le point mobile D se trouve en P (donné). Joignons CN, BN, CP, BP . Par le point P menons les lignes PT, PR qui coupent BD en T et CD en R telles que BPT = BNM, CPR = CNM (les angles BNM et CNM sont donnés). On voit facilement, comme l'observe Whiteside [40], que le choix de ces directions pour PT, PR correspond au complètement du parallélogramme nécessaire pour utiliser le Théorème 2 par le point A qui correspond au point à l'infini de la ligne MN.
Par hypothèse on a donc MBD = NBP et MCD = NCP. Si l'on soustrait les parties communes, on a NBM = PBT et NCM = PCR. Il s'ensuit que le triangle NBM est semblable à PBT et le triangle NCM est semblable à PCR . On a donc
PT : NM = PB : NB et PR : NB = PC : NC.
| Mais PB et NB sont donnés, ainsi que PC et NC. Il s'ensuit que le rapport |
|
et donné. |
En conséquence du Théorème 2 le point D décrit une conique.
Pour la partie réciproque nous utiliserons une nouvelle figure. [41]
|
Figure 15
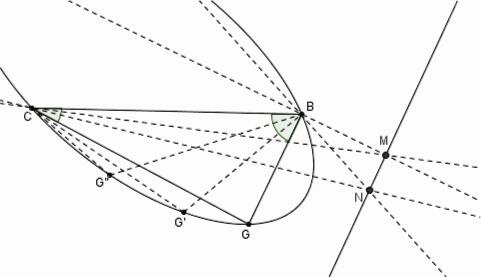 La démonstration de la construction organique 2 |
Donc, en prenant deux autres points G', G'', avec les mêmes angles, par les intersections des autres côtes [43] on détermine les points M, N, et donc une droite MN. On démontre facilement que, si D est un point arbitraire de la conique projeté par les côtés CD, BD des angles donnés tournants, les autres côtés se coupent en un point D' sur la ligne MN (voir la Figure 16). [44]
|
Figure 16
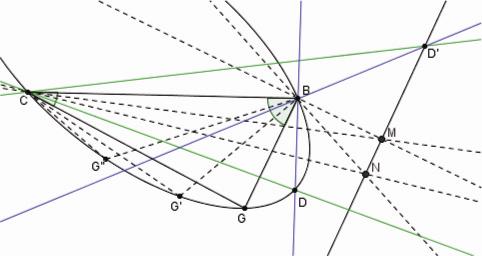 La démonstration de la construction organique 3 |
6.3 Une comparaison avec les Principia
L'incohérence des contenus de la Section 5 dans les Principia a été observé plusieurs fois. Newton lui même avait projeté d'en disposer les résultats dans un traité spécifique sur la géométrie des Anciens en le séparant des questions dynamiques et physiques. [45]
Nous ne voulons pas donner ici une analyse détaillée des différences entre la Solutio problemati Veterum de Loco Solido et le texte de la Section 5 des Principia, [46] mais simplement proposer quelques observations fonctionnelles à notre exposé.
En premier lieu, il faut souligner que Newton a cherché à atténuer le caractère de la Solutio, clairement consacrée à opposer à la solution cartésienne du problème de Pappus à quatre lignes la vraie (à son avis) solution des Anciens. [47] Le titre de la Section devient Inventio Orbium ubi umbilicus neuter datus et, dans la mesure du possible, loci solidi et conicæ deviennent trajectoires. [48]
Certains résultats qui ont un caractère plus explicitement projectif ne trouvent plus place dans le texte des Principia. En fait ils sont très intéressants en eux mêmes, mais leur importance pour les trajectoires des planêtes ne semble pas évidente, même à Newton.
Un bon exemple est donné par la Proposition 12.
Théorème (Prop. 12)
Si deux lignes CD, BD en tournant autour des points donnés C, B coupent deux autres lignes données de position HI, HK et les longueurs de ces lignes données de positions sont réciproquement déterminables par simplicem geometriam : [49] le lieu d'intersection de deux lignes mobiles D sera une conique qui passe par les points C, B autour desquels elles tournent. [50]
|
Figure 17
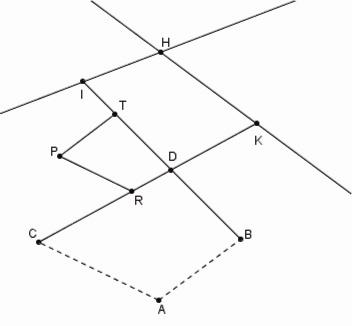 La Proposition 12 |
Sur la Figure 17, A et P et PR // CA , PT // AB . Les lignes PR et PT sont données de position et HK est déterminé par PR par simplicem geometriam (c'est à dire que il y a une relation bilinéaire entre HK et PR ). Cette relation s'étend à HI et donc à PT. [51] Si le point D vient à coïncider avec P , PR et PT deviennent nuls simultanément. [52] Si le point D vient à coïncider avec A, PR , et PT deviennent dans le même temps infini. [53] Il s'ensuit que le rapport est donné. Le Théorème 2 nous assure que D décrit une conique.
La démonstration de ce théorème a un caractère projectif bien plus évident que les démonstrations des théorèmes précédents. En fait, ces considérations sur les limites sont spécifiques de la géométrie projective naissante et n'ont rien à faire avec la géométrie des Anciens, bona pace de Newton.
7- L'Arithmetica Universalis
Dans l'Arithmetica Universalis, après la solution du problème de déterminer une conique par cinq points, une solution semblable à celles que nous avons vues, Newton propose une solution «per Algebram solam». [54] Aux yeux d'un lecteur moderne la chose peut paraître banale. Mais en fait il s'agit d'une des premières caractérisations d'une courbe algébrique, à partir de la forme de son équation, en imposant le passage par un certain nombre de points donnés.
|
Figure 18
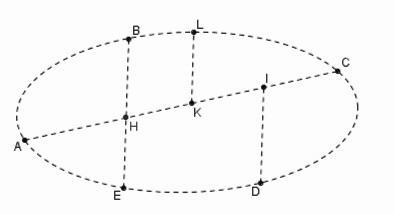
Une Conique par cinq points "per Agebram"
|
Les points A, B, C, D, E sont donnés. On joint AC et BE et soit H le point d'intersection. On trace DI parallèle à BE qui coupe AC en I . Une nouvelle ligne KL, parallèle à BE à son tour, coupe AC en K et la conique en L . Newton pose AK = x , KL = y et donne l'équation générale de la conique :
Après il déclare : « Supposons donc que le point L soit successivement en A, B, C, D, E et voyons ce qui s'ensuit.» [55] Si l'on a A ≡ F, en posant x = 0 et y = 0 dans (15) on a a = 0, ce qui réduit l'équation à
Un autre point convenable est évidemment C . Donc Newton pose AC = f, ce qui donne, en posant x = f et y = 0 dans (16), b = -cf. Ce qui suit après est tout à fait clair. Cependant cette solution de Newton représente un pas important vers l'algébrisation de la géométrie.
8- Les dernières années
Dans les dernières années de la carrière scientifique de Newton, le problème de Pappus acquiert un rôle différent : il n'est plus un objet à traiter individuellement, en opposant (plus ou moins explicitement) sa solution à celle de Descartes. Il vient à être considéré à l'intérieur d'un discours méthodologique plus large où le vrai objectif est celui de construire une mathématique qui hérite de l'esprit de la mathématique classique. L'analyse doit être seulement une étape préliminaire à garder pour soi par le mathématicien. La synthèse finale doit seule être exposée. [56] En outre, non seulement le style de la mathématique ancienne doit être préservé, mais, dans la mesure du possible, les outils eux même de cette discipline doivent êtré employés.
Un bon exemple est donné par la solution du problème de Pappus dans l'Analysis geometrica, un manuscrit de 1691 reproduit dans (MP, vol. 7, p. 200-221).
La solution est toujours réduite à la détermination d'un cinquième point en plus des quatre donnés naturellement par le problème, mais cette fois c'est la De sectione determinata qui entre en scène, probablement par le moyen des notices sur ce texte données par Pappus. [57]
|
Figure 19
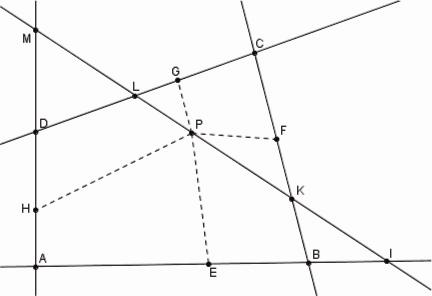 Newton et la De Sectione Determinata |
Le lignes AB, BC, CD, DA sont donnés aussi bien que les angles PEB, PFC, PGC, PHD et l'on demande
| que |
|
soit donné. Mais cette fois Newton ne mène pas une ligne par un sommet du |
quadrilatère. Il choisit une ligne arbitraire MI et il cherche un point P sur cette ligne. Les rapports
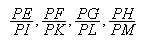
sont donnés. Donc (en employant pour commodité un peu d'algèbre), on a aussi les rapports donnés
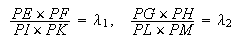
et donc
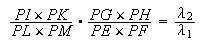
| Mais le rapport |
|
est donné. Soit |
|
.
Il s'ensuit que
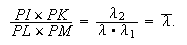
Nous sommes ramené au problème typique de la De sectione determinata. En termes modernes il s'agit simplement de résoudre une équation du second degré. [58] Encore une fois, Newton ne discute pas le fait qu'on a évidemment deux solutions.
9- Conclusion
Newton a toujours considéré le problème de Pappus comme équivalent à la détermination d'une conique par cinq points. Il a complètement ignoré l'existence de deux solutions peut-être en considérant le fait que le choix d'une région du plan conduit naturellement à la détermination d'une seule d'entre elles. Mais il n'a jamais explicité cette stratégie.
Toutefois ce problème lui a donné l'occasion de produire sa magistrale construction organique et, strictement connexe avec cette construction, la génération homographique des coniques.
Toutefois ces résultats, soit sont restés à l'état de manuscrits, soit ont été édités de manière inadéquate avant l'édition de Whiteside; ce qui ne leur a pas donné la possibilité d'avoir les conséquences mathématiques qui leur semblent inhérentes. En plus, la présentation des solutions du problème de Pappus comme la restauration de la « vraie mathématique » des Anciens a porté ombrage aux éléments novateurs. Si l'on regarde l'admirable Théorème 6, on voit que les éléments à l'infini ont un rôle considérable aussi bien que les relations bilinéaires. La connexion forcée aux mathématiques des Anciens a empêché ces travaux de trouver leur place propre dans le développement des mathématiques.
Références
M. Chasles : Aperçcu historique sur l'origine et le développement des méthodes en géométrie. Gautier-Villars, Paris, 1875. Seconde édition, conforme à la première.
R. Descartes : Geometria à Renato Descartes anno 1637 Gallice edita ; postea autem Unà cum Notis Florimondi De Beaune [. . .]. Operâ atque Studio Francisci µa Schooten[. . .]. Apud Ludovicum & Danielem Elzevirios, Amstaedami, 1659-61.
S. Di Sieno et M. Galuzzi : La quinta sezione del primo Libro dei Principia. Newton e il problema di Pappo. Archives internationales d'histoire des sciences, 39:51-68, 1989.
M. Galuzzi : I Marginalia di Newton alla seconda edizione latina della Geometria di Descartes e i problemi ad essi collegati. In (Belgioioso et al.,1990), pages 387-417, 1990.
M. Galuzzi et D. Rovelli : Nouveauté et modernité dans les mathématiques de Descartes. A paraître.
N. Guicciardini : Isaac Newton on Mathematical Certainty and Method, The MIT Press, Cambridge Massachusetts and London England, 2009.
N. Guicciardini : Reading the Principia. Cambridge University Press, Cambridge, 1999.
W. J. Greenstreet, éditeurs. Isaac Newton 1642-1727. London 1927. G. Bell and Sons LTD, 1927.
T.L. Heath : Apollonius of Perga. Treatise on Conic Sections. Edited in modern notation with introductions including an essay on the earlier history of the subject by T.L. Heath. Cambridge at the University Press, Cambridge,1896.
S. Maronne : La théorie des courbes et des équations dans la Géométrie cartesienne, 2007. Thése de doctorat de l'Université Paris 7 en Epistémologie, Histoire des Sciences.
J.J. Milne : Newton's contribution to the Geometry of Conics, in (Greenstreet, 1927), pages 96-114, 1927.
I. Newton : Philosophiae naturalis Principia Mathematica. Iussu Societatis regiae ac Typis Josephi Streater, 1687. Impression anastaltique Culture et Civilisation, Bruxelles, 1965.
I. Newton : Arithmetica Universalis ; sive de Compositione et Resolutione Arithmetica Liber. Typis Academicis, Cantabrigiae, 1707.
I. Newton : Mathematical Papers. Cambridge University Press, Cambridge, 1967-1981. Edited by D.T. Whiteside.
I. Newton : Principes mathématiques de la philosphie naturelle. Dunod, Paris, 2005. Preface de Voltaire. Traduction par la Marquise du Ch^atelet.
M. Panza : Newton et les origines de l'analyse : 1664-1666. Blanchard, Paris, 2005.
B. Pascal : Oeuvres complètes. Aux éditions du seuil, Paris, 1963. Préface d'Henri Gouhier. Présentation et notes de Louis Lafuma.
E. Sergio : Verità matematiche e forme della natura da Galileo a Newton. Aracne, Roma, 2006.
R. Taton : L'initiation de Leibniz µa la géométrie (1672-1676). Studia Leibnitiana Suppl., XVII, pages 103-129, 1978.
C. Taylor : An Introduction to the Ancient and Modern Geometry of Conics. Deighton Bell and Co, Cambridge, 1881.
H.W. Turnbull : The Correspondance of Isaac Newton, volume 1. Cambridge University Press, Cambridge, 1959.
D.T. Whiteside : Patterns of Mathematical Thought in the Later Seventeenth Century. Archive for history of exact sciences, 1:197-388, 1961.
Autre Ressource sur CultureMATH
Isaac Newton mathématicien : les années de formation et les premiers écrits, entretien avec Marco Panza