Lazare Georges Vidiani
Importer l'article (version pdf, 23 pages) - Ecrire à l'auteur
|
L'auteur, dans un style très personnel, ne cache rien de toutes les étapes de sa recherche, et des problèmes divers soulevés et fournit même une photo du bijou offert à Juel le 25 janvier 1925, pour son jubilé scientifique (ci-contre).
Utilisation dans l'enseignement : pour les classes préparatoires aux grandes écoles, en relation avec la théorie des surfaces et en illustration du groupe Psp4(F2) |
|
|
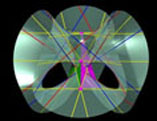
On trouvera une magnifique image en relief de la surface de Clebsch, réalisée par Alain Esculier pour l’article de Lazare Georges Vidiani, sur le site du Stéréo-Club Français (ci-contre en 2D). Cette image a remporté le 1er prix du Concours d'Images Scientifiques et Techniques 2006.
Cette image se trouve également sur le site personnel d'Alain Esculier (cliquer sur l'image ci-contre), ainsi que bien d'autres représentations et splendides calculs Maple (ici même). |
|
Les article de Lazare Georges Vidiani sur CultureMATH:
Le théorème de Juel
Racine carrée fonctionnelle
Les intégrales de Coxeter
Les épi ou hypo trochoïdes - images
Loi de groupe dans un triangle
Géométrie sur une Strophoïde
Critères d'Ermakov
Fermeture Hexagonale et le problème d'agreg (1947) qui va avec.
Le produit d'Hadamard de deux séries entières
Les motifs des pelages d’animaux - images
Loi de groupe sur une surface
Le problème des nombres gelés de Saint-Exupéry et l'énigme de la stèle du Pharaon qui va avec.
La Transformation du Boulanger
Problème des bœufs du soleil
La toupie Tippe-Top
Equations fonctionnelles
Jauge d'une cuve à Mazout
Le prix Steiner
Images offertes à CultureMath par l'auteur
Les motifs de pelages d'animaux
Voici quelques illustrations animées des modèles présentés dans l'article. Les visiteurs intéressés peuvent en demander d'autres à l'auteur.
|
|
|
|
|
panthère |
zèbre |
panthère rose |
arc-en-ciel |
Les épi ou hypo trochoïdes
Cet article propose un classement complet des courbes trochoïdales obtenues par roulement sans glissement. L'auteur donne un tableau à double entrée qui permet suivant les divers paramètres (rayons du cercle de base, de roulement et rapport d'élongation) de donner immédiatement la forme de la courbe. La recherche des développées de ces courbes est une application exploitée.
La théorie complète du Centre Instantané de Rotation est donnée en annexe et donne donc aussi une utilisation cinématique à cet article géométrique. Ces problèmes de roulement se retrouvent dans les problèmes d'engrenages.
Des simulations animées se trouvent par exemple sur le site de Robert Férréol http://www.mathcurve.com/courbes2d/epitrochoid/epitrochoid.shtml et celui d'Alain Esculier : http://aesculier.fr/ (aller à Rubrique, Maple).
En particulier sur http://aesculier.fr/fichiersMaple/wondergraph/wondergraph.html, on verra un jouet "extraordinaire" datant de 1910, le Wondergraph, qui permet de tracer des courbes plus générales que les épi- et hypo-trochoïdes, obtenues elles-mêmes pour certains réglages particuliers (remarque: pour les liens vers les publicités -du Wondergraph- cliquer avec le click droit de la souris et ouvrir, ou bien désactiver votre anti-spam).
Le wondergraph
Description
Fonctionnement
Animation 1: fonctionnement du wondergraph
Animation 2 : tracé d'une courbe