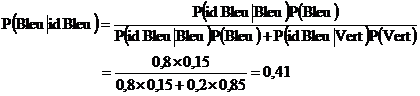Les psychologues Daniel Kahneman et Amos Tversky ont montré qu’en raison de toute une série de biais de jugement, les individus sont souvent incapables d’évaluer correctement les situations d’incertitude et d’appliquer les lois générales des probabilités, notamment la loi des grands nombres et la règle de Bayes[1].
La loi des grands nombres
Les individus ont beaucoup de mal à percevoir la loi des grands nombres. Les réponses données au problème suivant en sont l’illustration.
Il y a deux hôpitaux dans une même ville. Dans le plus grand, environ 45 bébés naissent chaque jour, alors que dans le plus petit, environ 15 bébés naissent chaque jour. Comme vous le savez, environ 50 % de tous les bébés sont des garçons. Cependant, le pourcentage exact sur une journée est variable : parfois, il est supérieur à 50 %, parfois inférieur.
Sur une période d’un an, chaque hôpital a enregistré les jours où plus de 60 % des bébés nés sont des garçons. Selon vous, quel hôpital a enregistré le plus de jours de ce type ?Réponses observées :
- Le plus grand : 22 %
- Idem : 56 %
- Le plus petit : 22 %Face à ce problème, une majorité de sujets ne perçoit pas la loi des grands nombres et n’applique pas la théorie des probabilités (qui doit leur faire répondre le petit hôpital), certains (22 %) restant même focalisés sur le grand hôpital, dans lequel il y a plus de naissances et donc moins de chance d’avoir des pourcentages disproportionnés de garçons et de filles…
La règle de Bayes
Le problème suivant montre la difficulté qu’ont généralement les individus à appliquer une autre loi fondamentale des probabilités : la règle de Bayes.
Un taxi est impliqué dans un carambolage de nuit. Deux compagnies de taxi, les Verts et les Bleus, opèrent en ville. On vous donne les données suivantes :
(a) 85 % des taxis en ville sont Verts et 15 % sont Bleus.
(b) Un témoin a identifié le taxi responsable comme Bleu.
Le tribunal a testé la fiabilité des témoignages dans ce type de circonstances (accident de nuit) et en a conclu que les témoins identifient correctement les couleurs dans 80 % des cas et se trompent dans 20 % des cas.
Quelle est la probabilité pour que le taxi impliqué dans l’accident soit un Bleu ?
La réponse médiane et modale est 80 %. Il semble donc que les sujets considèrent le jugement du témoin comme représentatif de la couleur du taxi et cela les conduit à confondre P(identifier Bleu |Bleu) = 0,8 (d’après les données du tribunal) avec la probabilité demandée qui est P(Bleu |identifier Bleu). Selon la règle de Bayes, cette probabilité est égale à 41 % puisque :
Le décalage tient au fait que la règle de Bayes prend en compte la probabilité a priori que le taxi soit bleu, P(Bleu) = 0,15, alors que cette grandeur est négligée par la plupart des sujets. Ces derniers font donc une erreur de jugement puisqu’ils sous-estiment voire négligent les probabilités a priori. Cette tendance générale à la sous-estimation des probabilités a priori a été confirmée par des études utilisant des dispositifs expérimentaux beaucoup plus sophistiqués. Par ailleurs, on observe généralement que l’apprentissage de la règle de Bayes par les sujets est lent.
Bibliographie :
Kahneman D., Slovic P. et Tversky A. [1982], Judgement Under Uncertainty: Heuristics and Biases, Cambridge University Press.
Tversky A. et Kahneman D. [1974], « Judgment Under Uncertainty: Heuristics and Biases », Science, 185, 1124-1131.
Note
[1] Daniel Kahneman, psychologue de l’Université de Princeton (Etats-Unis), a été récompensé du Prix Nobel d’économie en 2002 « pour avoir introduit en sciences économiques des acquis de la recherche en psychologie, en particulier concernant les jugements et les décisions en incertitude ». Son collègue Amos Tversky, décédé en 1996, a été largement associé à cette récompense.