Annexe 5 : Canevas construits sur des structures de satins carrés
Édouard Gand a développé une ingénieuse
méthode de composition des motifs décoratifs (ou
« armures-dessins ») à partir des
structures de satins carrés. Cette méthode est
exposée dans un article en deux parties du Bulletin de la société industrielle d’Amiens :
Nouvelles méthodes de construction des satins réguliers,
pairs et impairs. I : Théorie des nombres premiers
appliquée au pointé de ces armures (p. 57-88, janvier
1867). II : Armures-tissus ; armures-dessins ;
mosaïques (p. 257-300, juillet 1867).
Les propriétés de la disposition des points de liage
(« marche identique dans les deux sens »)
permettent de se limiter à une partie seulement de
l’armure pour placer les points de liage et construire le motif
décoratif. Il suffit ensuite de reproduire le dessin par
translations. Voici comment il explique cette méthode à
partir de l’exemple d’une armure de module 58 (voir figure
ci-dessous) :
« Cette marche identique dans les deux sens a cela de
particulièrement avantageux qu’elle dispense le
compositeur de poursuivre le pointé depuis le premier point jusqu’au cinquante-huitième
pour avoir l’exacte position respective de tous les liages. Il
peut conséquemment, pour commencer son opération, ne pas
pointer tout le plan compris dans le rapport d’armure, et se
contenter d’un fragment de l’échiquier dont la base
est imposée par ce rapport.
Ainsi, le plan qui suit (Fig. 57) n’est qu’une partie
du plan général d’un satin de 58. Mais la
quantité de points noirs que nous avons pu […] y jeter
très promptement, nous suffit pour commencer la composition de
quelque armure-dessin.
Nous venons de dire qu’en considérant un des points
de liage comme centre d’un motif quelconque et en reproduisant le
motif sur d’autres points pris à des distances
ingénieusement choisies, on arrivait à des
résultats souvent heureux comme dispositions
rythmiques » [opus cité p. 282]
|

|
[Gand 1867, II, fig. 57]
Satin carré de module p = 58 (on a un extrait seulement de l’armure).
Le décochement s’obtient en comptant la distance
qui sépare deux points noirs qui sont situés dans deux
colonnes contiguës (ou deux lignes contiguës). Ici, on compte
a = 17.
Remarque : les propriétés des satins carrés sont bien vérifiées.
p = 58 = 9 + 49 (somme de deux carrés)
a ² + 1 = 290, et 290 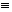 0 (mod. 58) 0 (mod. 58)
|
Édouard Gand propose dans son article une grande
variété de canevas ou
« armures-dessins » construits sur ce principe.
En voici quelques exemples (pour plus de clarté, les points de
liages sont représentés ici par des carrés rouges).
|

|
[Gand 1867, II, fig. 60]
p = 65
a = 8
|
|

|
[Gand 1867, II, fig. 61]
p = 82
a = 9
|
|

|
[Gand 1867, II, fig. 62]
p = 73
a = 27
|
|

|
[Gand 1867, II, fig. 63]
p = 34
a = 13
|
|

|
[Gand 1867, II, fig. 65]
p = 65
a = 18
|
|

|
[Gand 1867, II, fig. 66]
p = 34
a = 13
|
Retour au sommaire

![]() 0 (mod. 58)
0 (mod. 58)




