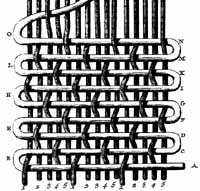
 |
Armure de Satin, article "Satin" de l'Encyclopédie de Diderot et D'Alembert |
Les tissus à texture rectiligne peuvent être représentés au moyen de dessins quadrillés, où les fils de trame sont représentés longitudinalement et les fils de chaîne transversalement. La duite est le nom donné aux passages de la trame à travers la chaîne. Le dessin des tissus réguliers se reproduit à l’identique par des translations parallèles aux axes figurant ces deux fils et il suffit de représenter le dessin de base sur un échiquier, en général carré, de taille minimale : ces dessins carrés portent le nom d’armures ; leur dimension p est le module de l'armure. Sur une armure sont figurés les points de liage correspondant aux points du tissu où s'opère la levée successive des fils de chaîne, à chaque insertion de duite (dans ses articles de 1867, Edouard Gand détaille les quatre armures fondamentales à fils rectilignes que sont la toile - ou drap - , le sergé, le batavia, et le satin). L'échiquier carré associé à une armure comporte un certain nombre de cases ombrées correspondant aux points de liage, les fils de chaîne étant représentés par les colonnes, ceux de trame par les lignes de l'échiquier.
Le satin régulier constitue le tissu le plus riche du point de vue arithmétique. D'après Lucas, sa construction obéit aux conditions suivantes :
« Le problème général de la construction de l'armure du satin régulier revient à placer dans les cases de l'échiquier carré de p² cases, p pions tels que deux d'entre eux ne se trouvent pas dans la même rangée horizontale ou verticale, et de telle sorte que, par rapport à un quelconque de ces pions (en supposant l'échiquier indéfiniment répété dans tous les sens), les autres pions soient toujours placés de la même façon. » [Lucas 1867, p. 3].
Pour faciliter la reproduction mécanique du dessin d'armure et en assurer l'esthétique, les points de liage doivent être ainsi régulièrement disposés selon des réseaux plans, invariants par les translations définies à partir de deux points quelconques du réseau. De plus l'armure du satin ne doit pas présenter de répétitions dans ses lignes ni dans ses colonnes.
Les conditions de réalisation d'un satin régulier se trouvent satisfaites par le choix d'un nombre a appelé le décochement, inférieur au module p et premier avec lui, qui permet la construction de deux suites :
- la suite des indices de colonne x = 0, 1, 2, 3, ... , k, ... , p-1.
- la suite des indices de ligne y = 0, a, 2a, 3a, ... , ka, ... , (p-1)a, ces derniers nombres étant calculés modulo p, donc dans Zp.
Un théorème d'arithmétique [Gauss 1801, p. 10] garantit que les restes (mod. p) des nombres y ainsi obtenus constituent une permutation des nombres {0, 1, 2, ..., p-1}.
Les points de liage sont figurés à l'intérieur du carré construit sur les entiers modulo p, soit dans Zpx Zp, à l'intersection de la colonne x = k et de la ligne y = ka (mod. p). Ainsi la réalisation de l’armure du satin de module 11 et de décochement 4 conduit au schéma vu ci-dessus, où les points de liage sont ombrés. Le décochement 4 correspond à l'ordonnée du point de liage situé dans la colonne 1.
Les propriétés d'un satin dépendent de la disposition de ses points de liages. Un manuel de tissage décrit en ces termes les qualités des satins selon la longueur de flottés (fils lâches) séparant les liages :
« L'armure satin donne un tissu plat, uni et brillant [...] En principe, plus un satin aura de flottés longs, plus il sera brillant, au détriment de la solidité du tissu, et, inversement, plus les liages seront rapprochés et les flottés courts, plus le satin sera mat et solide. » [Labriffe 1928, p. 340].