Les géomètres de la Grèce antique - Bernard Vitrac

Chapitre 6- Construire et comparer : les solides réguliers

Encart 2
Deux manières de construire l'icosaèdre : Euclide versus Pappus

 

Euclide, Livre XIII, Proposition 16	Pappus, Livre III, Proposition 57
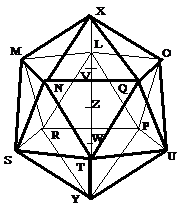
Euclide part d'une droite XY qui sera le diamètre de la sphère circonscrite. Son milieu, Z, sera donc le centre de la sphère. Il introduit une droite (ce qui suppose une analyse préalable) laquelle sera égale à la fois aux rayons des cercles circonscrits aux pentagones LMNQO, PRSTU, de centres respectifs V et W, ainsi qu'à la droite VW, distance entre les plans des deux pentagones parallèles. Il trace les cercles en question, décrit les deux pentagones réguliers, tête-bêche, d'où les points L, M, N, Q, O, P, R, S, T, U auxquels on adjoint X et Y. Ce seront les 12 sommets de l'icosaèdre. Le cœur de la (longue) preuve consiste à montrer que les droites telles que XM, MN, MS sont égales entre elles. Ainsi l'égalité des droites MN, MS résulte de 4 choses : • la distance des plans parallèles, VW, est égale au rayon du cercle circonscrit au pentagone LMNQO; • le point S se projette orthogonalement sur ce plan en un point S' milieu de l'arc MN. Autrement dit : MS' est le côté du décagone inscrit et S'S = VW = MV; • MS 2 = MS' 2 + S'S 2 (par I. 47); • Dans un cercle donné, le rayon (r = MV), le côté du décagone inscrit (c 10 = MS') et le côté du pentagone inscrit (c 5 = MN) vérifie : (c 5 ) 2 = (c 10 ) 2 + r 2 (XIII. 10). Et donc MN = MS. Euclide montre ensuite que l'icosaèdre est circonscrit par la sphère de diamètre XY. On voit qu'il est décrit comme reposant sur une "pointe" (le sommet Y).	P appus part d'une sphère donnée et procède par analyse et synthèse. Il suppose donc l'icosaèdre construit et, contrairement à Euclide, il le décrit comme posé sur l'une de ses bases. Il montre que l'on peut distinguer quatre triangles équilatéraux, égaux et tête-bêche deux à deux, d'une part ABC et LMN, d'autre part EDZ et GHK. ABC et LMN sont des faces de l'icosaèdre. Les triangles EDZ et GHK ont comme côtés les diagonales des pentagones associés à l'icosaèdre (mieux visibles dans la figure d'Euclide). I l vérifie soigneusement que ces quatre triangles sont parallèles entre eux, que les droites telles que DH, EG, ZK sont des diamètres de la sphère, puis que KHZ est un triangle rectangle. Ceci lui permet de montrer que les rapports EG : AB et EG : ED sont donnés. Comme le segment EG est un diamètre, il est donné. Les côtés AB, ED des triangles équilatéraux sont donc donnés, ainsi que les rayons des cercles circonscrits à ces triangles. Des cercles de rayons donnés décrits sur une sphère de diamètre donné ont des positions sur la surface de la sphère entièrement déterminées.   Et la synthèse, dit Pappus, est évidente.