Frédéric Brechenmacher - Centre Alexandre Koyré

Encart 5

Les types d’intersections des coniques et la décomposition polynomiale du déterminant.

1er type : 3 racines distinctes. D(l) = (l-a)(l-b)(l-c) et D1(l) = 1. 3 points d’intersection. Le faisceau contient 3 paires de coniques dégénérées distinctes représentées par les trois  couples de droites ci contre

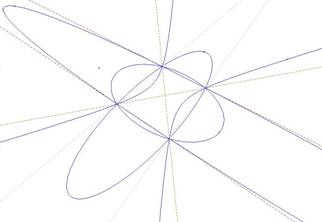
Sylvester caractérise cette situation de la façon suivante :

When there is no contact, we have as the types of their characteristics

U= x²+y²+z²

V= ax²+by²+cz²

The three roots of det(V+lU)=0 are l=-a, l=-b, l=-c,

Showing that there are three distinct pairs of lines in which the intersections of U and V are contained, the equations to three pairs being respectively :

(b-a)y²+(c-a)z² = 0,

(c-b)z² +(a-b)x² = 0,

(a-c)x²+ (b-c)y² = 0 ;

the four points of the intersection being defined by the equations corresponding to the proportions

x : y : z : : Ö(b-c) : Ö (c-a) : Ö (a-b) »

2e type (simple contact) : une racine double. Déterminant et mineurs sans facteurs communs. D(l) = (l-a)2(l-b) et  D1(l) = 1 Un point d’intersection double et 2 points simples.  Le faisceau contient 2 paire de coniques dégénérées distinctes : la tangente D et (BC) ainsi que (AB) (U+lV a deux valeurs propres distinctes).

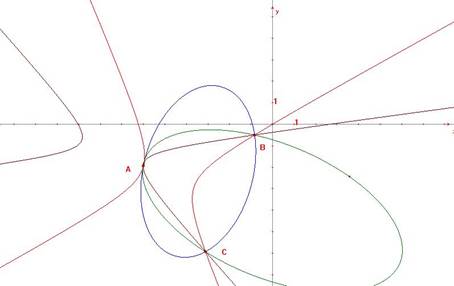
Sylvester caractérise cette situation de la façon suivante :

 Now let det(U+lV) have two equal roots ; the characteristics assume the form

U= x²+y²+xz,

V= ax²+by²+cxz

Two of the pairs of lines become identical, that is two of the four points of intersection coincide.

This may be termed ‘Simple contact ». The tangent at the point of contact is x=0 ; this equation making U and V each become of only one order.

The intersections are

x=0, y=0,

x=0 y=0

Ö (a-c)x+Ö (b-c)y = 0, z=0,

Ö (a-c)x- Ö (b-c)y=0, z=0. 

3e type (proximal contact) : trois racines doubles. Déterminant et mineurs sans facteurs communs. D(l) = (l-a)3 et D1(l)= 1 1 point d’intersection triple.  Le faisceau contient une paire de coniques dégénérées (la  tangente et la droite  (AB), U+lV a une valeur propre triple).

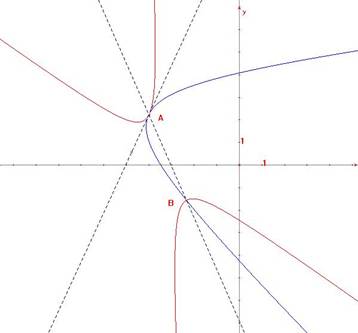
Now let det(U+lV) have all its roots  equal. This condition will be satisfied […] by making

U= x²+yz+yx,

V= ax²+ayz+byx

Here only one distinct pair of lines can be drawn to contain the intersections, showing that three out of the four points come together.

This may be termed « Proximal Contact. » The number of affirmative conditions to be satisfied is two, and the contact is therefore entitled of the second degree.

The tangent at the point of contact is y=0, and the four intersections become

x=0, y=0,

x=0 y=0,

x=0, y=0,

x=0 z=0. 

4e type (diploidal contact) : une racine double, déterminant et mineurs avec facteurs communs. D(l) = (l-a)2(l-b) et D1(l) = l-a 2 points d’intersections doubles.  Le faisceau contient 2 paires de coniques dégénérées distinctes : les deux tangentes et une droite double. (U+lV a deux valeurs propres distinctes).

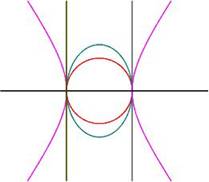
Let now the first minors of U+lV have a factor in common ; this will indicate that U+lV may be made to lose two orders by rightly assigning l, in other words, that the intersections of U and V be contained upon a pair of coincident lines. Here it is remarkable that the original forms of U and V reappear, but with a special relation of equality between the coefficients : we shall have, in fact,

U= x²+y² +z²,

V= ax²+ay² + bz²

This gives the law for double, or, as I prefer to call it, diploidal contact. By virtue of the Homaloidal law, we know that if three first minors of U+lV be zero, all are zero ; we have therefore to express that three quadratic functions of l have a root in common. This implies the existence if two affirmative conditions; the contact of the two conics taken collectively may therefore be still entitled of the second degree, although the contact at each of the two points where it takes place is simple, or of the first degree.

These points are evidently defined by the equation

{x+ Ö (-1)y =0, z=0},

{x - Ö (-1)y =0, z=0},

and the ordinary algebraical solutions of the equations U=0, V=0 would naturally lead to the four systems

x+ Ö (-1)y =0, z=0

x+ Ö (-1)y =0, z=0

x- Ö (-1)y =0, z=0,

x- Ö (-1)y =0, z=0

The two tangents at the point of contact are x+Ö(-1)y = 0, x-Ö(-1)y=0 and the coincident pair of lines containing the intersections is z² = 0.

5e type (confluent contact) : 1 racine triple, déterminant et mineurs avec facteur commun. D(l) = (l-a)3 et D1(l) = (l-a) 1 point d’intersection quadruple.  Le faisceau contient 1 paire double de coniques dégénérées : la  tangente en A  (U+lV a une valeur propre).

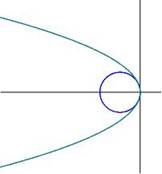
In the ordinary case of diploidal contact, the first minors having a factor in common, this factor will enter twice into the complete determinant of U+lV, but it may enter three times : this will indicate, that not only do the four intersections lie on a coincident pair of lines, but furthermore, that there is but one pair of lines of any kind on which they lie.

In the ordinary case of diploidal contact, it will be observed that this latter condition does not obtain ; the four intersections lie on a coincident pair of lines ; but they lie also on a crossing pair, namely, in two tangents at the point of contact. In this higher species of diploidal contact, it is clear that the two points of contact, which are ordinarily distinct, come together, and that all four intersections coincide.

This I call confluent contact ; the forms U and V corresponding thereto will be

U= x²+y² +xz,

V= ay²+axz

The common tangent at the point of contact being x=0, and the four coincident points x² = 0, y²=0.

The number of affirmative conditions to be satisfied being three, the contact is to be entitled of the third degree.

Observe, that it is of no use to descend below the first minors in this case ; because the second minors, being linear functions of l, could not have a factor in common, unless V :U becomes a numerical ratio, which would imply that the conics coincided.