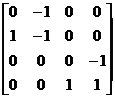Encart 3

Extraits de la démonstration du théorème de Jordan
dans le traité de Mac Duffee de 1943.

Let A and B be two square matrices, A of order r and B of order s. the matrix

A+B=

of order r+s is called their direct sum. […] More generally, let us suppose that the n×n matrix A of rank r can be written

A = A₁ + A₂+…+A_k =

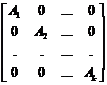where A_iis of order n_i and rank r_i. Let the row vectors of A span the space S, let the first n₁ two vectors of A span S₁, the next n₂ row vectors of A span S₂, etc. […] Thus S is the supplementary sum S₁+S₂+…+S_k of the subspaces S_i. [...] A subspace S₀ of S is said to be an invariant space of the matrix A if, for every vector Φ of S₀, it is true that A.Φ is in S₀. […] Much of the importance of invariant spaces derive from the following result

LEMMA . Let the total vector space S be the supplementary sum of the subspaces

S, S, …,S_k

where each S_i is of dimension r_i and has the basis σ_i, σ_i, …, σ_iri. Let P be the matrix whose column vectors are

(31).

If each space S_i is an invariant space of the matrix A, then

P^-1AP = B₁+B₂+…+B_k

where B_i is matrix of order r_i

[…] In general M can be written

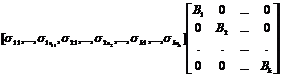
where each submatrix B_i has r_i rows and columns.

[…]

THEOREM 64. Let A be any n ×n matrix with elements in a field F, and let

m(x) ) m₁(x)m₂(x)…m_k(x)

be its minimum function expressed as a product of polynomials which are relatively prime as pairs. Let the null space of m_i(A) be of rank r_i. then A is similar to a direct sum

B₁+B₂+…+_k

where B_i is of order r_i, and the minimum function of B_i is m_i(x).

[…] Example :

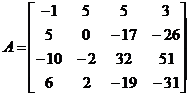
Let us choose Φ = (1,0,0,0). Then

P = (Φ, AΦ, A²Φ, A³Φ] =

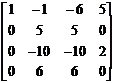[…] We find that

P^-1AP =

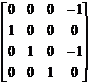which is the companion matrix of the minimum equation

m(x) = x⁴+x²+1=0

The second canonical form can be obtained from the matrix

B₁ =

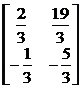B₂ =

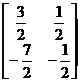Let

Q₁ =

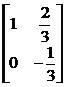Q₂ =

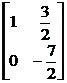Then

Q₁^-1B₁Q₁ =

Q₂^-1B₂Q₂ =

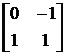are the companion matrices of the equations obtained from the respective factors x²+x+1 and x²-x+1 of the minimum function of A. Then A is similar to the matrix