Encart 14

Pincherle et la recherche de sous variétés d'un espace vectoriel invariantes par rapport à une homographie A.

[On] considère les substitutions linéaires comme des opérations (l’auteur dit opérateurs) appliquées aux vecteurs de l’espace ordinaire […]. Au même ordre d’idées, bien que le concept vectoriel n’y soit pas explicitement énoncé, se rattachent d’autres travaux importants : pour n’en citer qu’un, le mémoire de M. Frobenius sur les formes bilinéaires et les nombreuses recherches que ce beau mémoire à inspirées. […] L’objet de ce mémoire est l’étude des opérations distributives qu’on peut appliquer aux fonctions analytiques, plus particulièrement aux séries de puissances entières et positives de la variable x […]. Nous considérons l’ensemble de ces séries comme une variété ou espace (que nous appelons espace fonctionnel) à un nombre infini de dimensions : chaque série est un élément ou point de cet espace, et le système des coefficients de la série peut se regarder comme le système de ses coordonnées. [….] après quelques généralités sur les opérations distributives, on traite des racines de ces opérations, puis des opérations appliquées aux variétés linéaire à un nombre fini de dimensions, et au moyen du concept de racines d’une opération, on retrouve d’une façon tout à fait simple et naturelle la décomposition d’une homographie par les diviseurs élémentaires de Weierstrass.

Etant données l’opération A et la variété V(a₁, a₂,…,a_n) , invariante par rapport à A et qui ne renferme pas de racines de A, existe-t-il, dans cette variété, une fonction ω invariante par rapport à A ?

[…] Soit donc

ω = h₁a₁ + h₂a₂ +…+h_na_n

une fonction invariante par rapport à A; on aura

A(ω) = zω

[…] d’où suit pour z la condition nécessaire et suffisante d’être racine de l’équation caractéristique ou fondamentale de l’opération A par rapport à la variété donnée

[…] On démontre immédiatement que si V_n(a) contient une variété V_m(b),

m <n, qui est aussi invariante par rapport à A, et g(t) est le premier membre de l’équation fondamentale de A par rapport à V_m(b), g(t) est diviseur de f(t).

[…] A côté de l’opération A considérons l’opération

(11) (E_i = A-z_i, i=1, 2, …, q).

Nous savons que sa variété racine est la somme des variétés racines de . De plus nous pouvons dire qu’à cette variété appartiennent toutes les fonctions invariantes par rapport à A.

Nous nous proposons maintenant d’étudier les racines de l’opération B, et pour cela, celles de l’opération E^r, où E=A-z, et z désigne l’une quelconque des racines de (10).

[…] si l’opération E^p = (A-z)^p admet, dans la variété V_n(a), une racine propre ω^(p-1) on aura :

E(ω^(p-1)) = ω^(p-2), E(ω^(p-2)) = ω^(p-3),...,E(ω⁽¹⁾) = ω, E(ω) = 0,

d’où l’on tire :

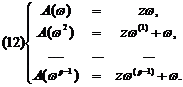
Les fonctions ω, ω⁽¹⁾, ..., ω^(p-1) ainsi déterminées sont linéairement indépendantes [...]. Si donc E^p admet dans la variété V_n(a) une racine propre ω^(p-1), il existe une variété d’ordre p,

V_p(ω, pω⁽¹⁾,…,ω^(p-1))

également invariante par rapport à A, contenue dans V_n(a), et sur laquelle A opère la substitution linéaire (12). Le tableau (12) montre que le premier membre de l’équation caractéristique correspondante est

g(t) = (t-z)^p,

d’où il suit que z est racine de f(t) de l’ordre p au moins.

[…]*

*Le lecteur a sans doute déjà remarqué que la théorie des opérations distributives nous a permis d’obtenir le concept des diviseurs élémentaires de Weierstrass, et cela, d’une façon excessivement simple. [Pincherle, 1899, 341].