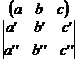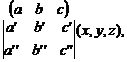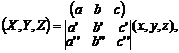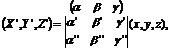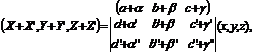Frédéric Brechenmacher - Centre Alexandre Koyré
Encart 12
Comparaison
des définitions des matrices chez Weyr et Cayley.
|
La
définition des matrices par Weyr. |
La
définition des matrices par Cayley. |
|
Eine Matrix nter Ordnung {ahk} oder A
auf ein System von n Werten x1,...,xn
oder kürzer (x) applicieren,
heiβt ein Werthsystem y1,...,yn mittelst der n linearen Gleichungen yh = ah1x1+...+ahnxn, (h=1,2,...,n) ableiten. Diese n Gleichungen mögen durch die symbolische Gleichung (y) = A(x) ausgedrückt werden. |
The term matrix
might be used in a more general sense, but in the present memoir I consider
only square and rectangular matrices, […] ;
in this restricted sense, a set of quantities arranged in the form of
a square, e.g.
is said to be a matrix. […] The notation
represents the
set of linear functions ((a,b,c)(x,y,z), (a’,b’,c’)(x,y,z),
(a’’,b’’,c’’)(x,y,z), so that calling
these (X,Y,Z), we have
|
Comparaison du calcul des matrices de Weyr
et
des opérations sur les matrices de Cayley.
|
Calcul des
matrices de Weyr. |
Opérations
sur les matrices de Cayley. |
|
Als summe zweier Matrizen nter
Ordnung A = {ahk},
A’ = {a’hk} wird jene Matrize B={bhk} bezeichnet, die auf
ein beliebiges System (x) appliciert das System (y+y’) ergibt, wobei (y) und (y’) die aus (x) durch A und A’ abgeleiteten
Systeme bezeichnen. Hieraus folgt sofort bhk = ahk+a’hk, d.h. die Elemente der Summe sind Summen
der correspondieren Elemente der Summanden. Eine Matrix, deren Elemente durchwegs
gleich Null sind, möge Nullmatrix heiβen und
mit O bezeichnet werden. Definiert man analog die Differenz
zweier Matrizen, so findet man A-A’=B falls ahk-a’hk = bhk (h,k = 1,2,…,n). Offenbar gilt A-A’+A’=A, A-A=0. Dans Symbol -A möge die Differenz 0-A
bedeuten; es hat demnach –A die
Elemente -ahk |
The equations
give
and this lead to
as a rule for the addition of
matrices ; that for their subtraction is of course similar to it. M±0 = M. the equation L=M, which
expresses that the matrices L, M
are equal may also be written in the form L-M=0,
i.e. the difference of two matrices is the matrix zero. 6. the equation
L=-M, written in the form L+M=0, expresses that the sum of the
matrix L, M is equal to the matrix
zero, the matrices so related are said to be opposite to each other; in other words, a matrix the terms of
which are equal but opposite in sign to the terms of a given matrix is said
to be opposite to the given matrix. |
Les
deux mémoires présentent la définition des éléments neutres 0 et 1, des
propriétés de commutativité de
l’addition, de l’associativité de l’addition et de la multiplication, et de la
distributivité de la multiplication sur l’addition. Eduard Weyr définit la matrice nulle après la définition de
l’addition, comme élément neutre ; la même remarque s’applique à la matrice unité [Weyr,
1890, 165], définie comme unique solution de l’équation AI=A pour tout A. Cayley,
au contraire, définit les matrices nulles et unités avant de donner les règles
d’opérations; la définition procède de la représentation sous jacente chez
Cayley d'une matrice comme une fonction
linéaire : la matrice nulle est la fonction qui transforme les quantités (X,Y,Z) en (0,0,0) et la matrice unité
la fonction qui laissent des quantités inchangées. Cette différence dans
l’organisation des propriétés du calcul symbolique manifeste une différence de
conception de la notion de matrice : pour Cayley, une matrice est une
représentation qui a "la forme d’un
carré", c’est une notion qui se "dégage naturellement de la notation
abrégée d’un ensemble d’équations linéaires" [Cayley, 1858, 475] ; pour Weyr, c’est un symbole dont il faut définir les propriétés
opératoires.